В смысле не сидит на синтетики, а торгует синтетическим инструментом (из трех компонентов).
Выпустил его с начала года в песочницу на депозите 250 т.р.
Понаблюдаю за ним годик, если попрет, то увеличу ему депозит.
Сделки очень часть закрываются в плюс. Вот одна из красивых сделок:




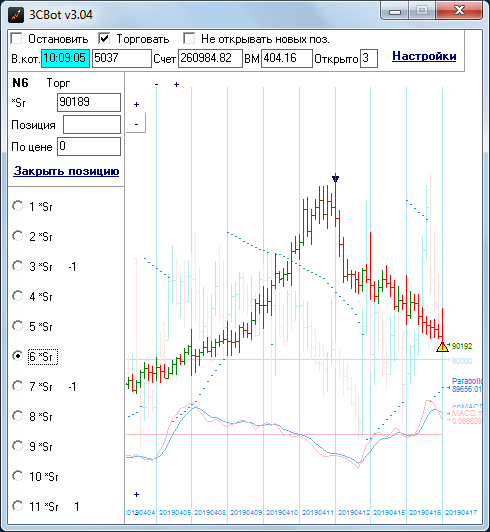
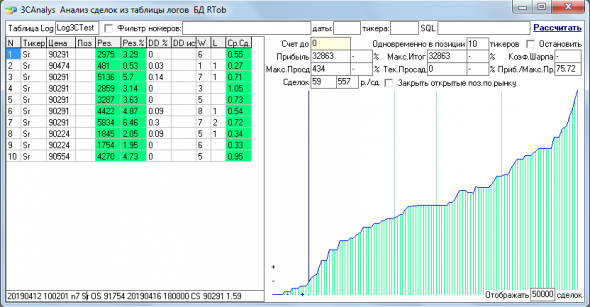
За первый квартал должно было получиться 32 863 руб. прибыли, и вот такая эквити:


( Читать дальше )

 

Введение

На сегодняшний день у меня есть три краткосрочные спекулятивные торговые системы и, соответственно, три одноименных торговых робота:

1. CandleMax
2. PVVI
3. AVP

Описание и тестирование в программе Wealth-Lab первых двух роботов я уже приводил. Вот соответствующие ссылки:

Тестирование рабочей свечной модели на исторических данных

Тестирование модели CandleMax в программе Wealth-Lab

Индикатор PVV (price/volume/volatility)

Тестирование робота PVVI в программе Wealth-Lab

Сейчас настало время дать краткое описание и привести тестирование в программе Wealth-Lab третьей торговой системы, которая у меня сейчас в работе.

Торговая система AVP (average volume/price) не является свечной моделью, как CandleMax, и не основана на красивой математической формуле, как система PVVI. Из трех моих спекулятивных роботов, робот AVP выдает сигналы реже всех. Тем не менее, результативность этого робота практически совпадает с результативностью робота PVVI, лишь совсем немного ей уступая.

( Читать дальше )

Приветствую!

Довольно часто, наблюдаю, что при создании алгоритмов, чаще прибегают к поиску прибыли через оптимизацию параметров, или не видя красивые «зеленные холмы» прибыли, просто сворачивают попытки развивать и насыщать алгоритм условиями. 
В примере ролика постарался продемонстрировать, возможно банальную попытку фильтрации, в основном идея для новичком.
Исходя из распределения дневных кластеров (объемы по ценам) «вырезаю сердцевину проторговки» и фильтрую по движению его границ. 
Другими словами, беру 50% проторговки цены и исходя из его динамики выявляю наличие тренда или его отсутствие, и тем самым фильтрую сделки по скользящим и по пробою уровня со стандартными параметрами. Все это работать может только при наличии тиковых данных, это нужно иметь ввиду, если решите повторить ролик. 


( Читать дальше )

Давайте соберем цену, потом разберем цену и сравним. Все будет производиться на ваших глазах в экселе. Файл, которого я прикладываю. ФАЙЛ https://cloud.mail.ru/public/27GB/5ipstzGrY  .(в зеленые области вы будите вписывать разные цифры).  Проверку на гетероскедастичность мы будем делать методом максимального правдоподобия. Во я загнул. Если просто. Мы возьмем две, хорошо известных нам стратегии и будем их прогонять на каждом шаге создания графика цены. Первая стратегия. Увеличение лота на один при убытке. Принцип опциона. И если у нас случайный процесс, то должно получаться 50/50. И удвоение позиции. Принцип мартингейта. И если у нас случайный процесс у=x^2, то у^2=x, мы всегда в плюсе. Давайте по шагам.

Шаг первый, лист W

Сгенерируем случайные числа. В экселе есть функция =случмежду(0;1). И 0 переведем в -1, а 1 в 1. У нас получился простой бинарный ряд из 1 и -1. Возьмем 100 таких цифр. Теперь посчитаем их сумму нарастающим итогом.  К сумме предыдущей прибавить следующее (Total). И построим график изменения этой суммы. Назовем это «геометрическое Броуновское движение».  Тогда, сумма всех случайных числе будет равна точке, куда пришел наш график. А сумма всех случайных чисел в квадрате, будет равна пройденному пути. А если каждый шаг происходит за 1 секунду. То это, одновременно, и время. И мы должны получить следующую зависимость. Берем 100, извлекаем корень квадратный и получаем 10. И это одно стандартное отклонение. И есть теорема, которая доказывает, что 68% траекторий  будут заканчиваться в диапазоне от -10 до +10. Вы можете это проверить сами. В графе ТЕСТ введите число. Если сумма средних от -10 до +10, ставим 1, если больше 0. У вас будет получаться среднее 0,7, в среднем. То есть в 3 случаях из 10 мы будем выскакивать из -10 +10. И это уже не 50/50 вверх или в низ. Это уже 30/70.

( Читать дальше )

Часть 1.

Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.

Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы)  или торговые системы.

 

Решение задачи состоит из двух этапов:

1. Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
2. Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.

 

Почему мы используем аналогию портфельной оптимизации с методами машинного обучения  — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации –  была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).

( Читать дальше )

Добрый вечер, коллеги!

Я хорошо понимаю, как мы всем здесь надоели с математическими выкладками, но все равно все это очень интересно. К тому же, это мой блог.

В комментариях к предыдущему баттлу А.Г. совершенно справедливо заметил, что для заработка на рынке нужно сначала убедиться, что рынок не является мартингалом. Ибо на траектории мартингала заработок любой ТС будет нулевым (без учета комиссий и проскальзываний) или отрицательным (с учетом комиссий и проскальзываний).

Теперь вспоминаем 2 моих предыдущих топика и смотрим на логнормальное случайное блуждание. Оно не является мартингалом и имеет положительное матожидание приращений. Однако практически на нем заработать нельзя (Эквити оптимальной ТС растет линейно, т.е. хуже любого депозита).

Можно придумать выпуклое преобразование случайного блуждания, на котором Эквити оптимальной ТС не будет расти даже линейно.

Например — берем случайное блуждание dx = sigma*dW
Пусть f(x)=1+x+x^2
Тогда df = (sigma^2)*dt + (2*x+1)*sigma*dW

( Читать дальше )

Вот в этой дискуссии я поддался общему настрою и согласился, что у логнормального случайного блуждания среднее приращений исходного ряда больше нуля. НИЧЕГО ПОДОБНОГО! Логнормальное случайное блуждание — это когда приращения логарифмов цен являются независимыми одинаково распределенными случайными величинами. НО! Исходным рядом для этого блуждания являются НЕ цены и их приращения, а ОТНОШЕНИЯ цен

C_t/C_t-1

Ничего удивительного, что у этого отношения математическое ожидание является положительным, так как и в числителе и знаменателе стоят положительные величины. Но только из отношения не перейти к разностям C_t-C_t-1

/*Более того, в силу однозначности логарифма легко доказать, что C₁,...,C_t,… — мартингал, тогда и только тогда, когда  LN(C₁),...,LN(C_t),… — мартингал.

(как правильно заметили в обсуждении, в общем случае я ошибся в этом утверждении, но оно верно в случае схемы Кэптейна C_t=C

( Читать дальше )

В ответ на пост smart-lab.ru/blog/532342.php
По-моему, 3 вариант лучше будет, торгуя правильной долей счета. 
Важно! Если нет переподгонки на истории и считаете, что показатели системы останутся примерно такими же в будущем.



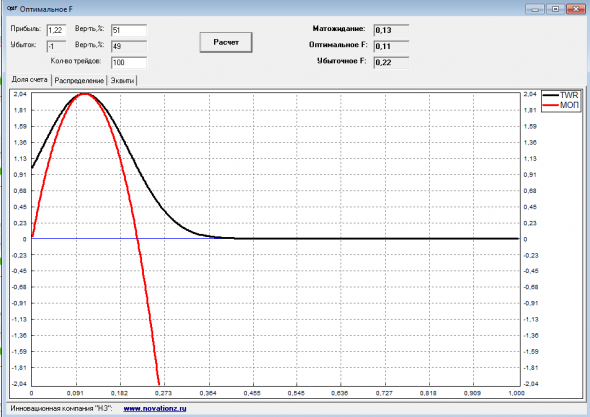
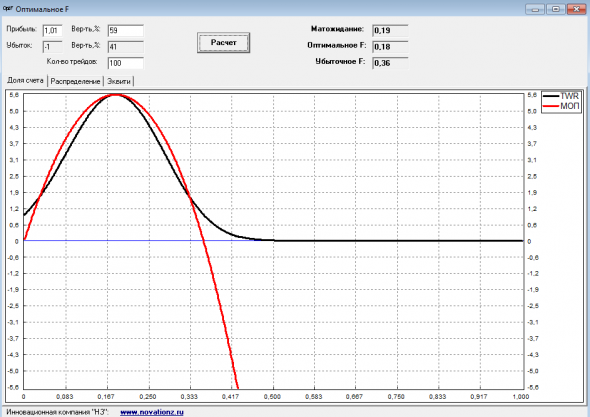
( Читать дальше )

В первой части мы рассмотрели «теорему о средней волатильности» где,  обозначили такое свойство:волатильности могут на разных таймфреймах значительно отличаться друг от друга. Но они всегда будут со временем сходится к одному  значению.

Вот, на этом свойстве и будет построен индикатор. Для индикатора нам нужны волатильности на различных таймфреймах. В качестве индикатора волатильности берутся два стандартных индикатора, но которые по сущности показывают одно и тоже.

Price Channel (PC) или ценовой канал. Индикатор представляет из себя две линии, которые ограничивают канал колебаний цены. Верхняя граница канала обозначает уровень локального максимума за прошедшие N периодов, а нижняя граница – уровень локального минимума за тот же промежуток времени. Таким образом, цена ограничивается максимальными точками колебаний – экстремумами за N периодов.

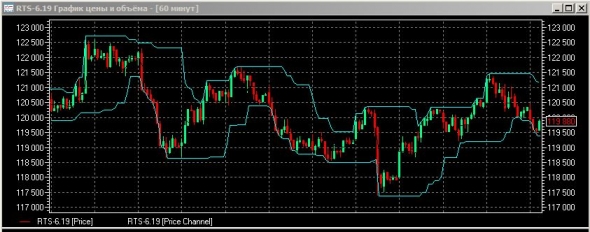
( Читать дальше )

Добрый день, коллеги!

Огромное спасибо всем, кто откликнулся!
Плодотворную дискуссию (пока) устроить не удалось, т.к. (как обычно):
— кто-то написал полную ересь
— кто-то написал умные вещи, но не в кассу
— кто-то бодро начал (за здравие), но не закончил (за упокой)
Отдельно очень приятно, что в ветке не было срача и хамства. Видимо, у всех горячих голов я давно в ЧС — и это не может не радовать.

Поскольку на верный ответ никто не набрел (ну или недобрел...), позволю себе его опубликовать.

1. Пусть S — обычное случайное блуждание процесс с нулевым МО и дисперсией sigma
    Тогда он описывается стохастическим уравнением

    dS = sigma*S*dW

2. Пусть L — логнормальное случайное блуждание
    Тогда по лемме Ито он описывается стохастическим уравнением

    dL = (-(sigma^2)/2)*dt + sigma*dW

    т.е. имеем обобщенный винеровский процесс со средним -((sigma^2)/2)*T и дисперсией (sigma^2)*T

3. Отсюда получаем формулу плотности для логнормального распределения (можно и в лоб посчитать, если нелениво)

( Читать дальше )