Блог им. Kot_Begemot
Портфельная оптимизация как бустинг на «слабых» моделях
- 09 апреля 2019, 23:20
- |
Часть 1.
Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.
Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы) или торговые системы.
Решение задачи состоит из двух этапов:
- Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
- Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.
Почему мы используем аналогию портфельной оптимизации с методами машинного обучения — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации – была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).
Это представление даёт нам право пользоваться сколь угодно неадекватными оценками доходности и риска (ковариации) в решении задач портфельной оптимизации лишь с тем ограничением, что в некоторой композиции они смогут получить максимально адекватный, устойчивый результат.
Прим. Отличие бустинга от бэггинга в том, что бэггинг собирает портфель (Bag) из адекватных, полноценных моделей, каждая из которых самостоятельно описывает действительность, в то время как бустинг, наоборот, пользуется неадекватными моделями, зависимыми друг от друга, самостоятельно действительность не отражающими.
В простой аналогии, если Bagging при решении вопроса проводит демократическую процедуру голосования среди полноценных членов общества, то Boosting, наоборот, идёт за решением вопроса в психиатрическую больницу.
Для решения задачи мы будем использовать MatlabFinancialToolbox, MatlabOptimizationToolbox, методы последовательного линейного и квадратичного программирования, MatlabStatisticsToolbox, MatlabImageProcessingToolboxи др.
Задачу будем решать в самом общем виде (подходящем для оптимизации портфеля любых активов, в т.ч. торговых систем). А именно:
- с учётом «без рисковой» ставки (ставки дисконтирования) 2% USD/year,
- ограничениями «buy only»,
- ограничением кредитного плеча равным 1,
- без ограничений оборота (Turnover=1),
- без обязательных резервов и ограничений диверсификации (LowerBounds=0),
- без учёта стоимости транзакций (Buy/Sell Costs= 0).
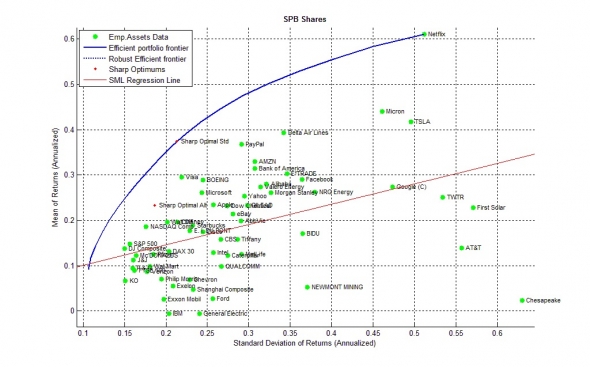
Рис.1. Точечная диаграмма исходных активов в плоскости доход-риск.
Мы имеем исторические котировки акций, торгуемых на Санкт-Петербуржской бирже за последние 6 лет и представленные 64-я основными активами. Эффективная граница Марковица (синяя линия), как ей и полагается, проходит через точку самого высокодоходного актива «Netflix» c уровнем доходности 60% годовых и «риском» 52% годовых и представляет из себя некоторое множество наилучших (с точки зрения доход/«риск») портфелей, которые можно было бы подобрать на исторических данных.
Среди всего множества лучших портфелей нам предстоит выбрать наилучший, в соответствии с критерием показателя Шарпа. То есть такой портфель, который позволял бы получить наибольшую доходность в условиях использования кредитного плеча с соблюдением ограничения по максимальной теоретической просадке. Этот портфель обозначен красной точкой на эффективной границе Марковица и обещает нам доходность 37% годовых, при рисках 22% годовых и показателе Шарпа 1.68 на год.
Тем не менее, валидационный тест (форвард тест) этот стандартный алгоритм выбора оптимального портфеля успешно проваливает, потому что оценки доходности и риска, полученные статистической обработкой данных (Mean-Covariance), даже если они робастные, являются неадекватными – как в узком смысле (то есть не способны прогнозировать поведение активов), так и в широком смысле (то есть на их основании не возможно составить оптимальный портфель).
И в этом нет ничего удивительного – стандартный алгоритм работает только на очень слабо дисперсионных, практически детерминированных данных, для которых стандартные оценки математического ожидания и дисперсии будут адекватными. В случаях же работы со стохастическими случайными величинами, стандартные оценки оказываются очень сильно смещены и, как показывает практика, к стохастическим данным стохастические модели в общем случае оказываются не применимы.
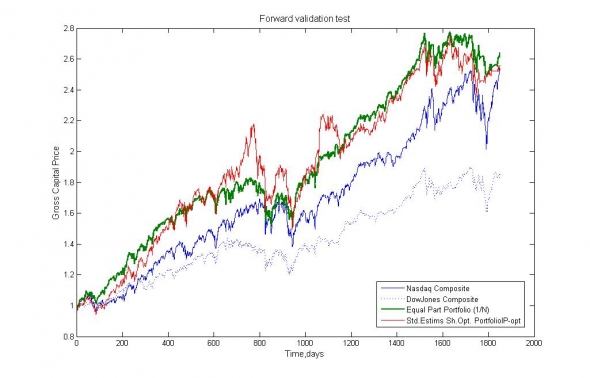
Рис.2. Сравнение динамики стоимости портфелей. Зелёная линия — среднее самих данных, красная линия — оптимизированный по стандартной процедуре (Mean-Variance) портфель.
Как видно из рис.2, даже с регуляризированной ковариационной матрицей (не L2-регуляризация), и робастной оценкой математического ожидания оптимальный портфель по Шарпу (красная кривая) не даёт возможности получить даже средних «по рынку» (зеленая кривая) показателей.
Далее мы будем обозначать этот портфель как «Std. Estims Sh.Opt Portfolio IP-opt», то есть как оптимальный портфель по Шарпу, полученный на стандартной оценке доходностей (среднее прошлых доходностей), с оптимальным инвестиционным периодом (IP-Optimal).
Подбирая другие, более адекватные, оценки будущих доходностей – линейной регрессией (Тrend), скользящей линейной регрессией (MoveTrend), а так же иными моделями, например угловыми оценками, и другими, более устойчивыми оценками ковариации, – можно добиться более приемлемых результатов.
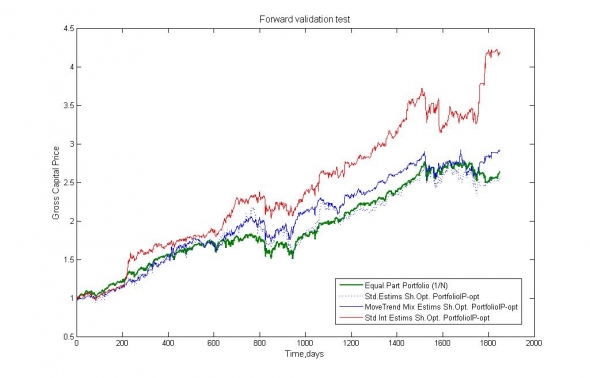
Этим путем нам удалось добиться улучшения показателя Шарпа в 1.26 раза (см. рис.3 и рис.4) по сравнению со средними по данным (средними по «рынку»), получив доходность 34% годовых при максимальной теоретической просадке 21.3%, то есть показателей, очень близких и даже лучших, чем апостериорная оценка параметров оптимального портфеля, построенная на исторически достоверных данных. Таким образом, подобранную композицию моделей оценки мы можем считать абсолютно успешной.
Рис.3. Сравнение динамики стоимости портфелей. Зелёная линия – данные, синяя линия – портфель, подобранный на трендовых оценках доходности, красная линия – портфель, подобранный на стандартных оценках доходности и устойчивых оценках ковариационной матрицы.
Рис.4.
Лучшее решение «Std. Int. Sh.Opt. Portfolio IP-opt» :
В качестве оценки доходности мы берём обычное, не триммированное, смещённое математическое ожидание доходностей за предшествующие 360 календарных дней, в качестве оценки ковариации – некоторую сглаженную (фильтрованную) ковариацию с определённым коэффициентом Калмана (в нашем случае используется не стандартная процедура), лагом кросс ковариации равной нулю и инвестиционным периодом 31 календарный день.
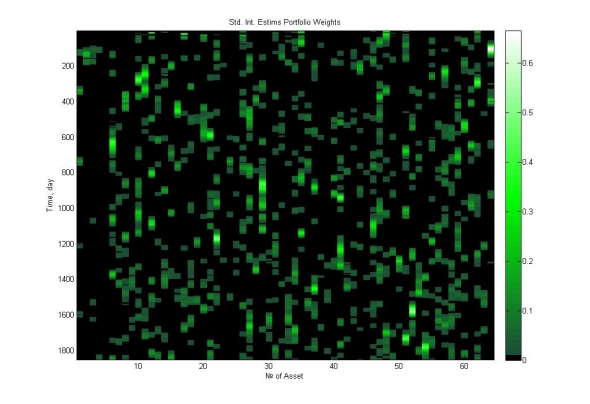
Рис.5 показывает динамику доли актива в портфеле в зависимости от времени, текущему сверху вниз. Если в вертикальном ряду есть отдельные “капли” – значит, актив попадает в портфель нечасто, и долго там не удерживается. Если наблюдаются “струйки” – значит, актив удерживается в портфеле длительный период.
Рис.5. Диаграмма весов активов в лучшем портфеле, демонстрирующая широту диверсификации и частоту перевложений в зависимости от времени (сверху вниз).


теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика





















Дык это ж курвфиттинг в чистом виде!