Блог им. Kot_Begemot |Теория и Практика Дельта-Хеджа
- 26 января 2020, 12:41
- |
Для того, чтобы продать волатильность, нам необходимо продать стрэддл — этим, мы полностью избавляемся от чувствительности к направлению движения цены, оставляя при этом чувствительность к «волатильности»… Чтобы не запутаться, обозначим первую волатильность за IV (Implied Volatility) и будем считать её заранее известной и эффективной.
Если бы рынок был монеткой и выходил бы на экспирацию двумя возможными вариантами {+IV, -IV }, то результатом продажи нашей опционной конструкции был бы ровно 0, в силу равенства IV=RV. Но рынок выходит на экспирацию через «тренды» и «пилы», которые выводят Базовый Актив в том числе далеко за ± IV, и в том числе и в ноль. В результате, конечное отклонение от ± IV и, соответственно, риски, которые мы принимаем при продаже стрэддла, составляют приблизительно :
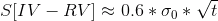
где S — СКО, RV ( «реализованная волатильность») - отклонение цены на экспирацию, t — время до экспирации, а сигма0 — величина шага движения цены. Это уравнение можно получить численно, а можно, взяв интеграл по соответствующему распределению Гаусса (аналитический вариант).
( Читать дальше )
- комментировать
- ★29
- Комментарии ( 41 )
Блог им. Kot_Begemot |Критерий Келли через нормальное распределение
- 20 января 2020, 21:27
- |
Ещё до того как я познакомился с критерием Келли, я уже успел наработать собственную широкую базу риск-оценок. И вопрос отказа от этого критерия для меня был, по сути, риторическим, тем более, что Келли, как бы мы того не хотели, достаточно примитивный (упрощённый) критерий. Но прежде чем отказываться от критерия хорошо бы вообще понять что это такое, учитывая, что критерий представляет весьма простое решение сложной задачи и интересен именно этим.
Для примера возьмём игру с нулевым E, в которой выигрыши распределены равномерно, с вероятностью 50/50 и представлены множеством {+50%,-50%}. За некоторое количество повторений, например за два раунда, мы будем иметь следующее распределение финансового результата:
- 25% случаев — выигрыш 125% капитала до 2.25 (два выигрыша подряд)
- 25% случаев — проигрыш 75% капитала до 0.25 (два проигрыша подряд)
- 50% случаев — проигрыш 25% до 0.75 (один выигрыш и один проигрыш)
Рассчитав статистические моменты этого распределения легко убедиться, что средний выигрыш, как это положено, будет равен нулю, а наиболее вероятный вариант (мода) будет представлен проигрышем 25% капитала. Теперь, если варьировать ставку, можно убедиться, что с ростом ставки математическое ожидание по крайней мере не снижается, а мода, то есть наиболее вероятный исход — падает.
( Читать дальше )
Блог им. Kot_Begemot |Контроль рисков в играх с рекапитализацией
- 04 ноября 2019, 20:28
- |
Сложность задачи контроля рисков состоит в том, что риски в действительности не ограничены и нарастают с течением времени так, что превращают бесконечно длительные игры с полной рекапитализацией в игры с абсолютно неконтролируемым риском. В связи с чем, задача выбора оптимального плеча (объёма) становится в общем случае математически не решаемой, а риск-менеджмент, в конечном счете, определяется только психологическим комфортом управляющего или инвестора. Тем не менее, исходя из некоторых предпосылок мы можем ограничить зону допустимого психологического комфорта и склонности к риску, то есть указать на некоторые их разумные пределы.
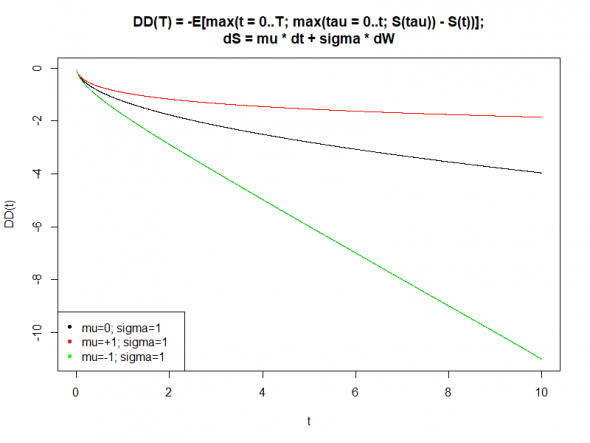
Изображение зависимости средней ожидаемой максимальной просадки заданных стратегий от времени. Любезно позаимствовано у Eugene Logunov.
Как и ранее, имея стартовый капитал 50 млн. долларов США мы будем пытаться обыграть господина Баффета, имеющего 500 млрд. долларов США, то есть будем стараться увеличить свой капитал в 10 000 раз за счёт игры на бирже. Играть мы будем нелинейно, то есть будем увеличивать ставки после каждого удвоения пропорционально текущему капиталу и поэтому для реализации нашей цели нам предстоит выиграть у господина Баффета не 10 000 раз подряд, а всего лишь:
Мы знаем, что наша стратегия обладает преимуществом над стратегией господина Баффета и позволяет играть против него с вероятностью 55%/45%, то есть с 10% смещением (Шарп = 1.6)
( Читать дальше )
Блог им. Kot_Begemot |О применимости АКФ в анализе временных рядов на примере акций ПАО Сбербанк
- 13 июля 2019, 14:22
- |
В свете интереса к моим работам в области оценки рисков нестационарных объектов со стороны опционов и возникшего вопроса о применимости к анализу финансовых временных рядов методов классического статистического анализа проведём маленький численный эксперимент:
- Оценим АКФ акций ПАО Сбербанк за последние 8 лет :
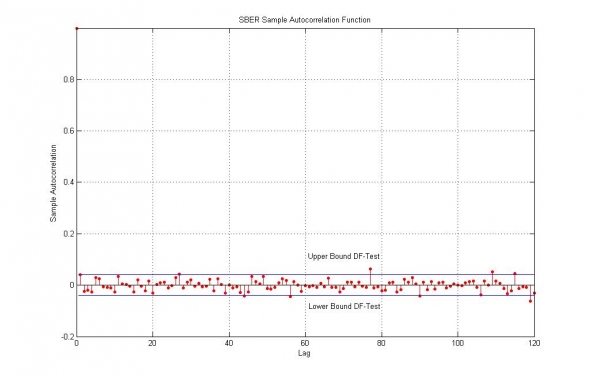
Рис. 1. Тест Дики-Фуллера и автокорреляционная функция логарифмических приращений цен акций ПАО Сбербанк.
Как видно из теста, никаких трендов (англ. тенденций, закономерностей) на акциях Сбербанка классической математической статистикой не обнаружено и все АК коэффициенты лежат в пределе статистической погрешности при измерении нуля.
Однако, тест Дики-Фуллера, с одной стороны, разработан для стационарных, не-локализованных процессов и отражает только отсутствие трендов в среднем по времени, а с другой — проводится совершенно с другими целями выявления детерминированных сезонных и/или растущих тенденций, а не стохастических оценок рисков. В этом смысле мы будем интерпретировать АКФ не по-классически, детерминированно, а как функцию искажения случайности.
( Читать дальше )
Блог им. Kot_Begemot |Глобальные оценки инвестиций - стресс-тест и адекватная оценка риска (численный эксперимент).
- 15 апреля 2019, 08:22
- |
В задачах оценки бизнес проектов, прогнозирования спроса, определения справедливой цены опциона или портфельного инвестирования, так или иначе, возникает проблема адекватной оценки рисков. Обычно за риск принимается простое, выборочное среднеквадратичное отклонение, для которого хорошо разработан аппарат математической статистики, позволяющий прогнозировать критические показатели, например просадки, и проводить стресс-тесты в предположении центральной предельной теоремы, то есть в предположении узкой стационарности наблюдаемых процессов.
Однако, мы зачастую имеем дело с абсолютно другими, нестационарными процессами. Не стационарность процесса может быть вызвана как нелинейным синергетическим эффектом (реклама и «сарафанное радио», мода, политические выборы, революции и пр. самоорганизации), как множественностью состояний системы (тренд/флэт), так и просто некоторой инерцией системы, связанной, например, с задержкой принятия решений основными игроками.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- ецб
- золото
- инвестиции
- инфляция
- китай
- коронавирус
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опек+
- опрос
- опционы
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- финансы
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- шорт
- экономика
- юмор
- яндекс


















