Избранное трейдера FullCup
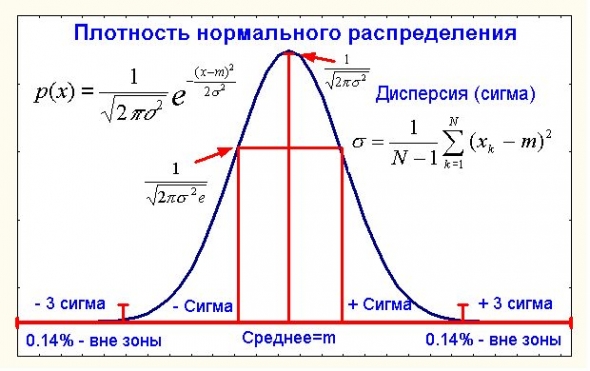
О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)
- 16 октября 2018, 16:41
- |
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам. Что такое центральная предельная теорема в ее классическом виде?
Пусть нам дана некоторая сумма большого числа случайных величин Х=х1+…+хN где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.
Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если xi – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x
( Читать дальше )
- комментировать
- 8.5К | ★72
- Комментарии ( 215 )
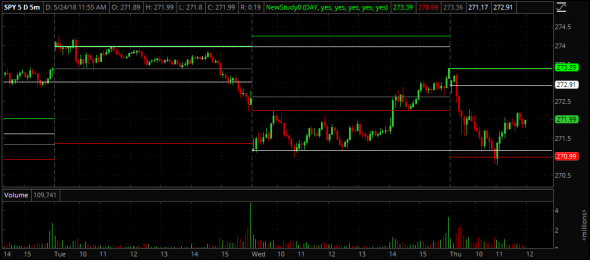
Индикатор ThinkOrSwim рисует на графике линии вчерашних Hi, Low, Close, Open и сегодняшнего Open
- 15 октября 2018, 19:44
- |
Рисует линии вчерашних Hi, Low, Close, Open и сегодняшнего Open на графике
Очень удобно, наглядно показывает важные уровни вчерашнего дня.
#Thinkorswim studies
#Рисует линии вчерашних Hi, Low, Close, Open и сегодняшнего Open на графике.
#Thinkorswim https://radchenkovy.com/thinkorswim-live
input sPeroid = {default DAY, WEEK, MONTH};
input iHigh = {default "yes", "no"};
input iLow = {default "yes", "no"};
input iClose = {default "yes", "no"};
input iOpen = {default "yes", "no"};
input iTodayOpen = {default "yes", "no"};
plot pHigh = if !iHigh then high(period = sPeroid)[1] else Double.NaN;
plot pLow = if !iLow then low(period = sPeroid)[1] else Double.NaN;
plot pClose = if !iClose then close(period = sPeroid)[1] else Double.NaN;
plot pOpen = if !iOpen then open(period = sPeroid)[1] else Double.NaN;
plot pTodayOpen = if !iTodayOpen then open(period = sPeroid)[0] else Double.NaN;
pHigh.SetDefaultColor (Color.GREEN);
pHigh.SetPaintingStrategy(PaintingStrategy.DASHES);
pLow.SetDefaultColor(Color.RED);
pLow.SetPaintingStrategy(PaintingStrategy.DASHES);
pClose.SetDefaultColor (Color.GRAY);
pClose.SetPaintingStrategy(PaintingStrategy.DASHES);
pOpen.SetDefaultColor (Color.WHITE);
pOpen.SetPaintingStrategy(PaintingStrategy.DASHES);
pTodayOpen.SetDefaultColor (Color.WHITE);
pTodayOpen.SetPaintingStrategy(PaintingStrategy.DASHES);;Полная библиотека индикаторов, фильтров и сканеров для Thinkorswim в этом блоге bit.ly/2vKq4F8
Старый гном в одном посте
- 15 октября 2018, 11:34
- |
Гном. Или как трейдер обанкротил банк.
Глава первая и вторая
Глава третья и четвертая
Глава пятая и шестая
Гном 2. Возвращение.
Глава первая
Глава вторая и третья
Глава четвертая и пятая
( Читать дальше )
- комментировать
- 20.5К |
- Комментарии ( 57 )
Как обогнать индекс (пример выигрышной торговой стратегии)
- 15 октября 2018, 09:37
- |
Как обогнать индекс (пример выигрышной торговой стратегии)
В кругу экономистов бытует мнение, что обогнать фондовый индекс на длительной перспективе невозможно, и если вам удалось в какой-то определенный год вырваться вперед, получив прибыль гораздо выше той, которую продемонстрировал индекс акций, то в будущем неизбежно ваши результаты не превзойдут индекс, а могут оказаться только хуже него. Подобная точка зрения следует из гипотезы эффективного рынка. К сожалению, экономика отличается от математики тем, что строгое доказательство практически любого утверждения представляется невозможной задачей. Тем не менее, в данной статье мне бы хотелось привести пример одной из стратегий, которая способна обогнать индекс акций в длительной перспективе. Разумеется, я отдаю себе отчет в том, что не могу доказать это математически. Впрочем, в экономике практически везде используются различные гипотезы, которые невозможно доказать, например, почему-то принято считать, что движение цен подчиняется нормальному распределению, и я что-то нигде не встречал какого-либо доказательства подобного утверждения. Тем не менее, именно на основе гипотезы о нормальном распределении была придумана знаменитая формула Блэка-Шоулза для оценки стоимости опционов, за которую ее авторы даже получили нобелевскую премию.
( Читать дальше )
Книга Китайское исследование. Сильно впечатлен. Интересные сведения про рак.
- 13 октября 2018, 19:23
- |
 Итак, я прочел всего 120 стр из 380, пока летел в Новосибирск, но мыслей так много, что решил не откладывать на потом.
Итак, я прочел всего 120 стр из 380, пока летел в Новосибирск, но мыслей так много, что решил не откладывать на потом. Допустим мой пост прочтет 2000 человек. По статистике, из них 1000 человек помрет от сердечно-сосудистых, и около 300 из этих человек от онкологии.
Думаю, что при такой выборке, к сожалению, найдется среди читателей человек, у которого в той или иной стадии есть онкология. Если онкология дошла до этапа (3) прогрессии, то повернуть вспять ее будет уже почти невозможно. Надеюсь, среди вас таких нет. На этапе инициации (1) канцероген проникает в ДНК и повреждает ее. Я думаю, что в наших организмах это происходит периодически, но это ничем плохим не заканчивается. А вот на 2-м этапе поврежденные (мутировавшие) ДНК либо размножаются либо погибают. Стадия промоции, пока она не перешла в 3 этап, обратима. Развитие процесса зависит от того, чем мы питаем организм. Есть вещества, которые питают раковые клетки, — т.е. выступают стимуляторами, а есть вещества, которые напротив, для развития опухолей являются антистимуляторами.
Идея книги, что начальный процесс, если он у вас не дай бог есть, можно повернуть вспять,
Книгу написал ученый Колин Кэмпбелл на основании больших научных исследований, которые делал он и его аспиранты, а также другие приглашенные ученые. Первые 120 страниц написаны очень научно, очень логично, что у меня не возникло никаких сомнений в их правдивости или подозрений в манипуляции данными. Да, возникло много вопросов, которые я тоже опишу. Забегая вперед, скажу, что у книги Кэмпбелла есть иного несогласных критиков, например тут (сам пока на читал).
Итак, в чем главный тезис?
Животный белок и животный жир провоцирует рост раковой опухоли.
Итак, что я понял? Чтобы вызвать рак, нужно:
1. канцероген. Их дофига. Кэмпбелл использовал афлатоксин.
2. катализатор. Как раз в качестве катализатора использовался животный белок (казеин, из которого на 87% состоит молоко).
Опыты проводили на мышах.
Насколько я понял, канцероген+катализатор образуют особо опасные соединения, чем по отдельности.
Мышам давали огромную дозу афлатоксина, потом кормили животным белком — 20% рациона или 5% рациона.
Так вот сколько бы афлатоксина не давали, от рака печени дохли в основном те мыши, которые питались животным белком. Статистически значимым был порог в 10% рациона. Если животный белок превышает 10%, то резко растет развитие опухолей. Причем растительный белок глютен такой реакции не давал, сколько его не увеличивай.
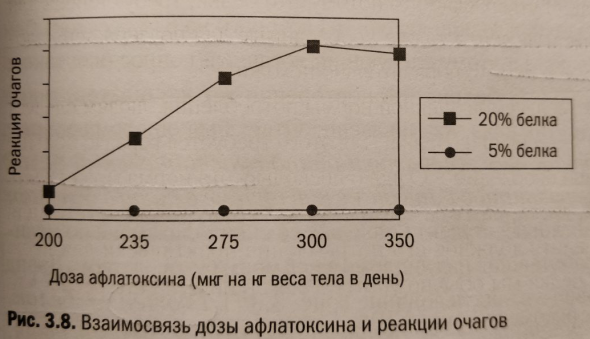
На этом этапе возникло сразу несколько вопросов:
1. Что если именно афлатоксин + казеин дают такую химическую реакцию? А если канцероген другой, то результат будет другим?
2. Что если канцероген другой? Что если животный белок использовать не казеин а другой?
3. Опасен только животный белок? А что же на счет например сахара или быстрых углеводов?
4. Если мы понизим долю животного белка в рационе, то не понизим ли мы иммунитет, что приведет к другим болезням?
5. Если нет канцерогенов (а ведь мышам давали реально много афлатоксина), то являются ли животные белки опасными?
Автор ответил на пару этих вопросов, проведя ряд других экспериментов. В качестве канцерогена использовались вирус гепатита Б (HBV), и связка HBV+20% казеиновая диета дала тот же результат на печени. Кроме того, брали мышей с раком молочной железы и кормили казеином. Результат оказался тот же.
Один из интересных выводов книги — только 2-3% онкологических случаев связаны с генетикой. И на 97% с условиями жизни и питания.
Лично я сделал такой вывод, что долю животного белка и жира надо отказываться с возрастом, потому что риск онкологий в юном возрасте минимален, поэтому смысла жертвовать здоровьем детей, кормя их травой, нет.
Важный маркер — ваш уровень холестерина в крови. Он растет вместе с потреблением животного белка/жира. Чем больше холестерина, тем выше риск развития и сердечно-сосудистых и онкологии.
У меня холестерин 5,42 ммоль/л. Год назад было 4,79. Верхняя планка 7, желательно иметь ниже 5,18. В сельских районах Китая 3,3 ммоль/л. Увеличение в рационе растительных продуктов приводит к снижению уровня холестерина.
Будьте здоровы!
Продолжение следует.
Мысли
- 13 октября 2018, 09:16
- |
Имея за своей спиной большой объем информации о различных историях трейдеров, давно сделал вывод, что часто и даже очень трейдинг рассматривается трейдерами, как возможность относительно быстрой и легкой (лопатой махать не надо) наживы. Здесь несколько аспектов.
1. Трейдер изначально нацелен на значительное обогащение. Значит, его трейдинг отличается торговлей высокорискованными инструментами, а, значит, рискованной торговлей.
2. Трейдер нацелен на стабильность получения доходов от трейдинга. Для меня самый оптимальный тип трейдеров. Такой трейдер хорошо должен просчитывать риски, иметь опыт, знания, умения по трейдингу, торговать незначительной частью своего депо, целиком посвящая себя трейдингу (последнее не мое). Такому трейдеру особо безразлично качество инструментов по их рискованности.
( Читать дальше )
А крутите вы статистику так, как пытаюсь крутить ее я? =)
- 12 октября 2018, 19:34
- |
Введение
Вообще, на мой взгляд, однозначно полезно вести статистику и тщательно за ней следить в различных разрезах. Это может быть и разрез рынка и разрез результатов вашей торговли. Как то на заре моего осознанного трейдинга, один мой более опытный коллега (Глеб, привет), сказал: «Вообще у рынка есть несколько показателей, которые характеризуют рынок: ликвидность и волатильность. И их вариация характеризует стадии рынка.» Это было около пяти лет назад. А помню и более того, применяю, до сих пор.
Пример
Я вот например придумал для себя показатель ликвидности. Вычисляю средний объем сделки за сессию в том или ином стакане.
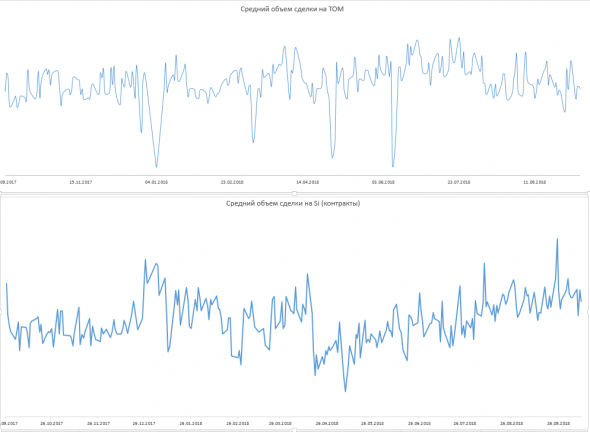
Как можно увидеть, ликвидность стакана на споте практически не меняется. А показатель на срочке после апрельских событий резко просел и очень и очень долго восстанавливается. Как минимум, если у вас какие то алго для срочки, то в такие моменты в массе случаев нужно было реагировать и применять меры.
( Читать дальше )
Д е Ш и Ф р О в Щ и К.
- 10 октября 2018, 05:12
- |
«Да, такова была моя участь с самого детства»
М.Ю. Лермонтов, «Герой нашего времени».
Помню, со школьной скамьи меня волновали вопросы, на которые мои сверстники не обращали внимания. К примеру, когда изучали «Евгения Онегина», меня озадачили такие строчки:
«Кто жил и мыслил, тот не может
В душе не презирать людей»
Я пытался понять, почему так, спрашивал друзей, но они даже думать в этом направлении не хотели. А я пытался разгадать, заучил наизусть все места в романе, где Пушкин размышляет о жизни, периодически их декламируя для себя и стараясь проникнуть в глубинный смысл пушкинских строк.
Помню, кто-то принёс в школу задачку из «Наука и Жизнь». Нужно было заполнить квадрат из 100 клеток, шагая так, как ходит конь в шахматах. Целый месяц почти все решали на уроках эту головоломку. Максимально кому-то удалось дойти до цифры 86. Я тоже увлёкся, но не мог побить рекорд. Тогда я первый раз задумался, что к решению задачи надо подходить с разных сторон. Я перестал тупо заполнять клетки, в надежде, что мне повезёт и я побью рекорд, а стал смотреть на квадрат и думать. Недолго думая, я обнаружил, что задачу можно упростить, разбив квадрат 100 на 4 квадрата по 25 клеток. Если я смогу заполнить квадрат в 25 клеток и перейти в следующий, то это значительно упрощает задачу и экономит время в 4 раза. Пока другие тратили время на заполнение 100 клеток, я сосредоточился на 25. В течении часа я решил эту задачу и объявил в классе, что заполнил все 100 клеток. Я чувствовал себя победителем, испытывал чувство эйфории победителя.
( Читать дальше )
Напишу робота
- 09 октября 2018, 17:34
- |
Готов написать робота под вашу стратегию.
Требования:
1. Небольшое количество параметров (если вы оцениваете момент входа по 100500 критериям, это не особо интересно)
2. Четкая формализация
3. Подтвержденная доходность
Ограничения:
1. Qlua
Предпочтения:
1. Спот
2. Фьючи
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал