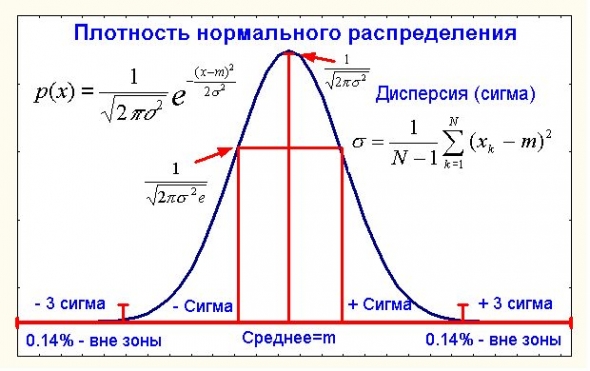
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Возник вопрос: покупать или продавать SNGS?

С одной стороны ценная бумага существенно недооценена, при цене 26,98 руб. P/E (средняя прибыль за 2015-2017) — 3,99, P/B (B-по полугодию) — 0,27, с другой стороны интересна динамика. Выполнил анализ пятилетней доходности.

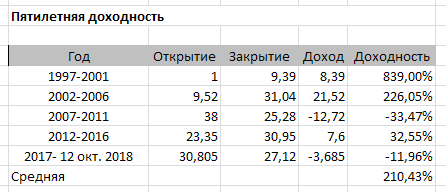
Итоги конечно воодушевляют, но как отнестись к последним 12 годам?

Решил сделать анализ годовой доходности (инвестиции в начале года, выход — в конце). Вот, что из этого получилось.


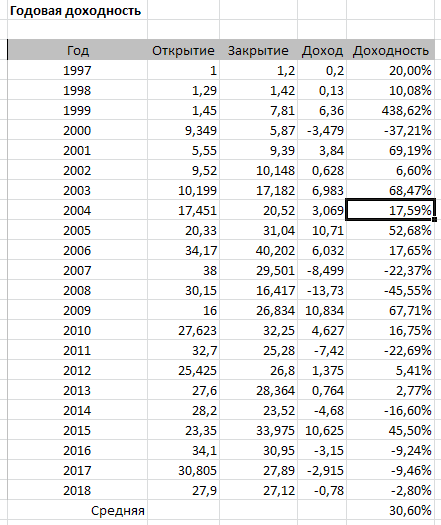
( Читать дальше )

Недавно нашел интересный график, который позволяет по новому взглянуть на недавние нырки фондовых рынков. 



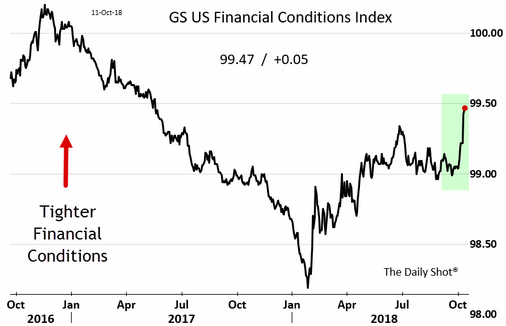
       Это график финансовых условий в Америке, или говоря по простому, насколько легко получить финансирование. Их него следует, что буквально за последние полторы недели произошло стремительное нарастание до нового максимума. Причем величина изменений значительна — она превышает диапазон колебаний за последние пол года. Другими словами буквально за несколько дней с деньгами стала твориться напряженка.
      На этом фоне недавний обвал по S&P не только не кажется неожиданным, но и даже необходимым. 

      Причин такого стремительного изменения я не знаю. Версия о том, что ставки подорожали, и это привело к снижению доступности денег  — не проходит. Из графика видно, что индекс опережал падение облигаций. Сначала стало меньше денег, а потом стали падать облигации. А еще затем рухнули акции. Далее по списку. Например, меня впечатлила распродажа высокодоходных облигаций в США, которые еще совсем недавно были хитом.

( Читать дальше )

Как обогнать индекс (пример выигрышной торговой стратегии)

          В кругу экономистов бытует мнение, что обогнать фондовый индекс на длительной перспективе невозможно, и если вам удалось в какой-то определенный год вырваться вперед, получив прибыль гораздо выше той, которую продемонстрировал индекс акций, то в будущем неизбежно ваши результаты не превзойдут индекс, а могут оказаться только хуже него. Подобная точка зрения следует из гипотезы эффективного рынка. К сожалению, экономика отличается от математики тем, что строгое доказательство практически любого утверждения представляется невозможной задачей. Тем не менее, в данной статье мне бы хотелось привести пример одной из стратегий, которая способна обогнать индекс акций в длительной перспективе. Разумеется, я отдаю себе отчет в том, что не могу доказать это математически. Впрочем, в экономике практически везде используются различные гипотезы, которые невозможно доказать, например, почему-то принято  считать, что движение цен подчиняется нормальному распределению, и я что-то нигде не встречал какого-либо доказательства подобного утверждения. Тем не менее, именно на основе гипотезы о нормальном распределении была придумана знаменитая формула Блэка-Шоулза для оценки стоимости опционов, за которую ее авторы даже получили нобелевскую премию.

( Читать дальше )

Нарисовал несколько идентичных графиков за период с 30.03.2018 по 14.10.2018 по Сбербанку на основании данных https://www.moex.com/ru/contract.aspx?code=SBRF-12.18 о

1. Цене закрытия
2. Кол-ва открытых длинных позиций физ. лицами
3. Кол-ва открытых коротких позиций физ. лицами
4. Кол-ва открытых длинных позиций юр. лицами
5. Кол-ва открытых коротких позиций юр. лицами





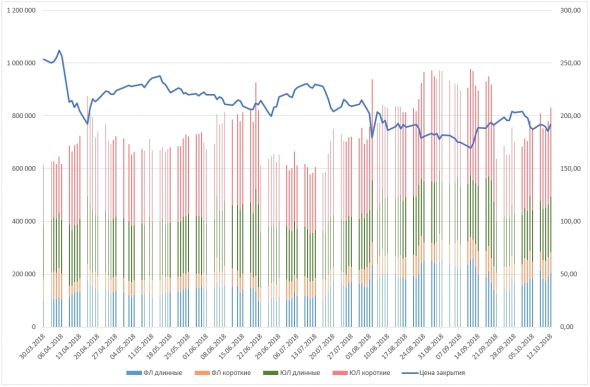
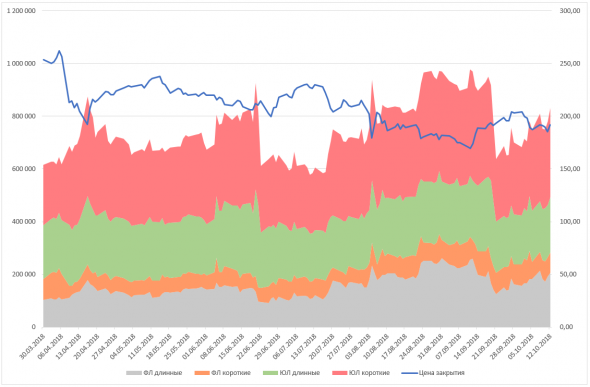
( Читать дальше )

Введение

     Вообще, на мой взгляд, однозначно полезно вести статистику и тщательно за ней следить в различных разрезах. Это может быть и разрез рынка и разрез результатов вашей торговли. Как то на заре моего осознанного трейдинга, один мой более опытный коллега (Глеб, привет), сказал: «Вообще у рынка есть несколько показателей, которые характеризуют рынок: ликвидность и волатильность. И их вариация характеризует стадии рынка.» Это было около пяти лет назад. А помню и более того, применяю, до сих пор.

Пример

     Я вот например придумал для себя показатель ликвидности. Вычисляю средний объем сделки за сессию в том или ином стакане.

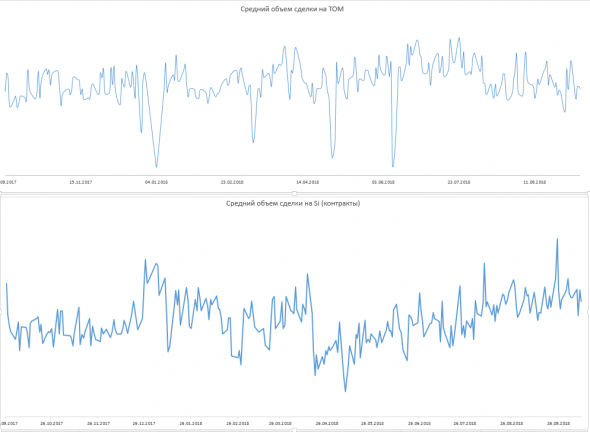
     Как можно увидеть, ликвидность стакана на споте практически не меняется. А показатель на срочке после апрельских событий резко просел и очень и очень долго восстанавливается. Как минимум, если у вас какие то алго для срочки, то в такие моменты в массе случаев нужно было реагировать и применять меры.

( Читать дальше )

Уже в 2011- 2013 гг. некоторые аналитики, инвесторы и трейдеры стали задумываться о том, что быстрый рост капитализации «Магнита» содержит в себе отдельные составляющие «пузыря». 

Они обращали внимание, что основным драйвером роста капитализации компании почти всегда была премия за будущий рост компании. 
А когда к премии за будущий рост бизнеса добавилась премия за будущий рост капитализации, возник механизм надувания пузыря. 

Механизм надувания этого пузыря:
1. Компания растёт.
2. Инвесторы дают акциям премию за будущий рост компании.
3. Поэтому капитализация растёт быстрее самой компании.
4. Инвесторы видят, что капитализация растёт быстрее компании и начинают давать премию акциям уже и за ускоренный рост капитализации.
5. Пока ожидания инвесторов выполняются, механизм работает.
6. Как только показатели компании ухудшились, и ожидания перестали выполняться, начался выход инвесторов.
7. Это ещё больше ухудшило динамику акций, чем ускорило дальнейшее сдувание капитализации и превратило его в панические распродажи.

( Читать дальше )

Наткнулся на книгу, блуждая по национальной электронной библиотеке. 
Биржа и спекуляция 1878

Что бы заинтересовать одна из страничек

Уже более недели американские акции падают синхронно с облигациями.
Это сильнейшее падение капитализации, что всегда крайне опасно для перекредитованных игроков. Очень вероятно, что сегодня в среду у некоторых кончились деньги и они были вынуждены отстопится. Что и привело к нырку S&P под полтора процента. 

Причин называлось много. От поднятия ставки ФРС, до итальянского популизма. Все это верно. 
Но мне более всего нравится конспирологическая теория, что началась атака Китая на американский долг. Напомним, что уже проходило сообщение о выводе первых трех миллиардов из американских казночеек. Что вполне может быть только вершиной айсберга и только началом. Ведь он уже давно намекает на асимметричный ответ в торговой войне в США. И у него как раз кончились симметричные аргументы. 

Эта новость удивительным образом совпала с российским решением о дедолларизации. 

Как бы то не было, но теперь не только короткие биллы показывают рост доходностей, но и длинные бумаги начали смотреть на юг. Все происходит в согласии с событием на горизонте времени около 30 лет в виде пробоя нисходящего тренда доходностей.

( Читать дальше )

Доброго времени суток смартлаб! С Вами Чеширский.

Прежде всего, спасибо за такое большое кол-во положительных оценок моего предыдущего поста!
Мне очень приятно, что вам понравилось, честно. Не ожидал.

Отдельное спасибо за критику, кое-что я действительно забыл добавить в свои расчеты, но теперь справедливость восстановлена и это прекрасно.

В этом посте я поделюсь своими скромными наблюдениями и подсчетами. Возможно кому-то они покажутся интересными, а те, кто уже в курсе могут кинуть в меня помидором за боян. Поехали!

Есть такая замечательная контора Callan Associates Inc. Она занимается консалтингом в сфере инвестиций, консультирует всякие крутые фонды, предсказывает когда нас накроет тленом в очередной раз. Ну в общем как и все в консалтинге особо она нифига и не делает) Ладно, кое-что все же делает) А именно каждый год ведет свою индексную таблицу. Она известна как «Callan Periodic Table of Investment Returns». В нее вносятся результаты доходности основных индексов с 1998 года. И это, на самом деле, весьма интересная таблица! Практически наглядное пособие и мини-грааль в одном флаконе. Собственно вот она:

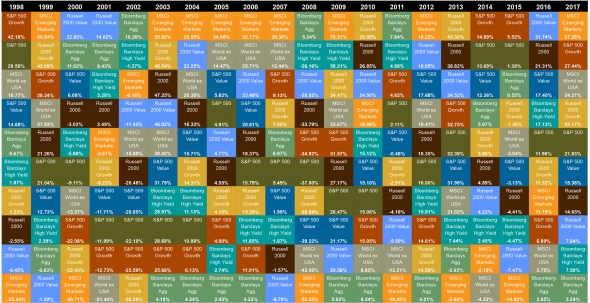
( Читать дальше )