Избранное трейдера Матвеич
Ответ грефу от настоящего Менеджера
- 20 октября 2018, 10:41
- |
- комментировать
- 6.2К | ★6
- Комментарии ( 188 )
Евробонды для нищих
- 19 октября 2018, 15:23
- |
Все мы знаем, что ставки по вкладам сейчас смешные.
И некоторые из нас знают, что на Московской бирже торгуются Евробонды, в том числе некоторые из них маленькими лотам от 1000$
Их мало, поэтому я потратил совсем немного времени на их анализ.
Статистика по объемам за 2 последние недели.
Субордов тут нет.
В принципе, если не боитесь ВЭБа, то можно себе подыскать бумажку с разной дюрацией, хотя мало кто сейчас захочет покупать длинные. И есть даже целая одна бумага в евро.

И в текстовом виде для удобного поиска по ISIN (извиняюсь за грязь)
| 1 | BIN-19 | XS1379311761 |
| 2 | Sistema-19 | XS0783242877 |
| 3 | TMK-20 | XS0911599701 |
( Читать дальше )
Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год! Часть 3 - Мой ответ Чемберлену!
- 19 октября 2018, 10:16
- |
27.07.2018 ИФНС 15 по г. Москве, было принято решение по возврате мне 52 000 рублей после прохождения камеральной проверки моей инвестиционной декларации по форме 3-НДФЛ, направленной 27.04.2018 года.
21.08.2018 мной с помощью сервиса «Личный кабинет» было сформировано заявление на возврат указанной суммы. Заявление было принято налоговым органом 21.08.2018 и зарегистрировано под № 15690-ЛКФЛ. С соответствии с действующим законодательством, денежные средства должны были поступить на счёт указанный в заявлении не позднее 20.09.2018.
К указанной дате средства не были перечислены, НИКАКОЙ информации из ИФНС 15 ко мне не поступало.
( Читать дальше )
Московский рынок недвижимости под давлением
- 18 октября 2018, 19:12
- |
На долю Московского рынка недвижимости приходится лишь около 4% ввода всей жилой недвижимости в России. Тем не менее именно он зачастую служит индикатором для рынка жилья России. Московский рынок недвижимости характеризуется снижением цен на жилье с 2013 года. Отчасти это связано с перегревом рынка во время финансового кризиса 2008 года, за трехлетний период перед которым цены на недвижимость в долларах взлетели в 3 раза до $6 тыс. за кв.м.

С конца 2014 года наблюдается существенное уменьшение цен на недвижимость в долларах до уровня 2006 года на фоне ослабления рубля из-за снижения цен на нефть и введения санкций против России. При этом стоимость квадратного метра в рублях сохраняется на уровне 170 тыс. руб. с 2014 года во многом за счет падения курса рубля к доллару в 2 раза с 2014 года.
( Читать дальше )
Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год! Часть 2 - Чудеса в налоговой!
- 18 октября 2018, 17:56
- |
Начались чудеса с налоговой! Продолжение истории - Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год!
Вчера я написал пост, о том что случилось с моим заявлением в ИФНС 15 о возврате 52000 рублей по ИИС (заявление было от 21.08.2018). Сегодня мне на почту приходит письмо с ответом на данное заявление., хотя по закону я должен был получить ответ (если он требовался, например тот же отказ) не позже чем, через 30 дней.
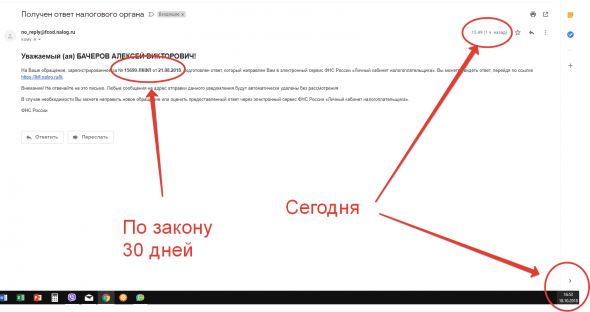
Напомню, что я писал письмо через сервис «Личный кабинет» — 01.10.2018 чтобы налоговая разобралась, что произошлом с моим заявлением от 21.08.2019, поскольку ни ответа не денег я не получил. Ответ на письмо от 01.10.2018 я получил вчера, он датирован 16.10.2018. Скрины приведены в предыдущем посте (https://smart-lab.ru/blog/499854.php). Получается, что ответ на само заявление о возврате я получаю позже, чем на письмо, в котором просил разобраться. Что я могу подумать в этот момент? Там будет примерно та же информация, т.е. год указан неправильно, и поэтому отказ (ровно как и в письме от 16.10.2018).
( Читать дальше )
А крутите вы статистику так, как пытаюсь крутить ее я? =) #2
- 18 октября 2018, 17:12
- |
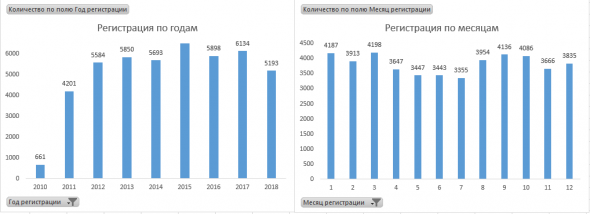
Вот я привел кол-во регистраций по годам. Цифра практически константа, то есть стабильно ~5500 человек
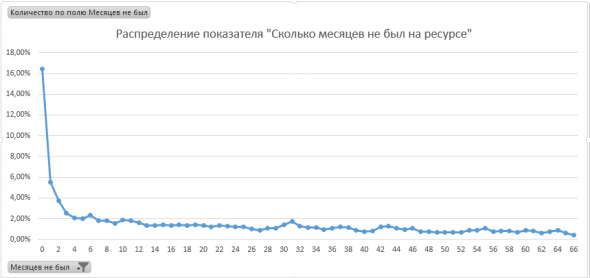
А вот я привел кол-во активных профилей на текущий месяц. Их получилось в районе 16%. То есть порядка 8000 профилей.
( Читать дальше )
Акции с высокими дивидендами в долларах США
- 17 октября 2018, 14:58
- |
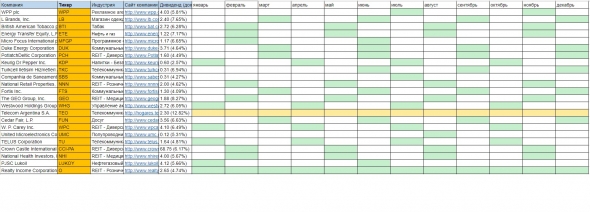
Ссылка на таблицу https://docs.google.com/spreadsheets/d/1bksfxH_ul41r9x9SQf5p6lnYVv1Fy22-hCc0jCiY-_s/edit?usp=sharing
Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год!
- 17 октября 2018, 13:53
- |
Теперь новая напасть. Как владелец иис, я возвращаю 52 000 рублей каждый год по ндфл. Делается это достаточно просто (по идее, и в этом году решили сделать ещё проще вроде как. в прошлом такой проблемы не возникало):
1.Вы сдаете декларацию 3-НДФЛ через тот же личный кабинет.
2.Она проходит камеральную проверку, и налоговый орган выдает решение о возврате (смотри скрин 1).

( Читать дальше )
Мой опыт работы с компанией «Investors Trust Assurance SPC» («ITA») или О чём промолчал ваш финансовый консультант
- 16 октября 2018, 18:03
- |
Мой опыт работы с компанией «Investors Trust Assurance SPC» («ITA») или О чём промолчал ваш финансовый консультант
Программы накопительного страхования от иностранных страховых компаний набирают все большую популярность на российском рынке благодаря, скорее, высоким бонусам финансовых консультантов за продажу полисов, чем реального удобства, доступа на широкие зарубежные рынки, и так называемой «стабильности и защищенности ваших средств». Я до сих пор не могу найти в интернете реальных и подробных отзывов об инструментах этой компании со стороны клиентов. В ответ на любой запрос по этой теме вылезают красивые статьи от финансовых консультантов, где все так хорошо расписано, что слюнки текут! Только сиди и жди счастливой пенсии лет через 15 и до конца дней своих! А между тем, тут и грабли, и подводные камни, и двойное дно…
Пишу свой отзыв с моим опытом работы, чтобы вы, будущий инвестор, «семь раз подумали», прежде чем ввязаться в эту историю.
( Читать дальше )
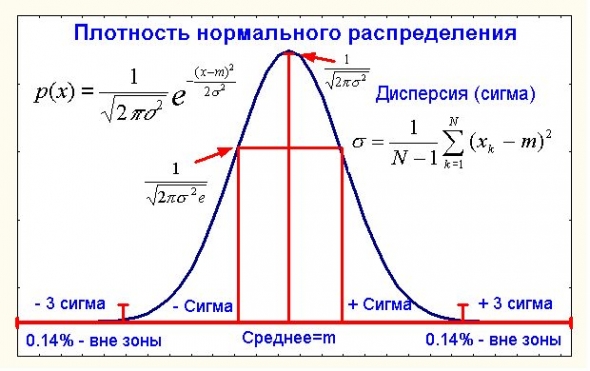
О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)
- 16 октября 2018, 16:41
- |
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам. Что такое центральная предельная теорема в ее классическом виде?
Пусть нам дана некоторая сумма большого числа случайных величин Х=х1+…+хN где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.
Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если xi – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал