0. Как говорится. пока горячо. Ну и, как было произнесено главным героем одного сильного отечественного фильма, «раки к драке».

1. Не люблю оффтопные посты, но позволю себе несколько строк. В порядке доброго бесплатного совета. Дисклеймер: я не расскажу как вылечиться от рака и не расскажу как заработать деньги.

2. Так сложилось, что у меня накопился неплохой опыт взаимодействия с онкопатологией в разных форматах, скажем так, из первых рук: хирургия, облучение, химия + некоторые современные гипотетические способы лечения в экспериментальном режиме.

3. Про не-Россию ничего не скажу. Скажу про Россию.

4. Деньги ничего не решают. Деньги могут упрощать некоторые нюансы борьбы с онкопатологией.

5. Решают связи. В узком смысле на некоторых этапах важны специфические личные связи, когда надо договориться, например, быстрее или в лучшие условия. В широком смысле связи решают вообще в плане кругозора, возможностей что-то организовать и тд.

6. Если складывается ощущение, что деньги могут решить вопрос (например, без денег вас не кладут в операционную, а за деньги готовы это сделать хоть сегодня), то, с вероятностью > 0.9, вас тупо бессмысленно порежут за ваши деньги.

( Читать дальше )

Взято из https://nakhusha.livejournal.com/45884.html

Мы никогда не можем полноценно представить себя через 30 лет. Но я вас уверяю, в 60 лет также хочется жить, как и в 30, если не сильнее. Но 60-летние часто живут с денежными привычками 20-летних. И, поверьте, от этого им очень горько на душе, что жизнь прошла, а они как пахали, так и пашут без возможности уволиться, потому что на пенсию не прожить, а сбережений нет.

Но даже у пенсионера, отягощенного каждодневным походом на ненавистную уже работу, есть выход. Всего лишь необходимо понять, что вариантов в жизни осталось мало, поскольку самого ценного ресурса (времени) уже почти нет. Значит, надо отсеять все лишнее и оставить одно-два самых сильных желания.
Если он хочет каждое утро не «чесать на работу», а попивать чаек на даче, не надо покупать на последние сбережения новый домик, строить забор, а стоит прикинуть, сколько есть средств, сколько они дадут прибавки к пенсии, найти работу полегче (на полставки, эпизодическую) и осуществить желаемое.

( Читать дальше )

Начались чудеса с налоговой! Продолжение истории - Как я возвращаю 52 000 по ИИС из налоговой в 2018 году за 2017 год!

 

Вчера я написал пост, о том что случилось с моим заявлением в ИФНС 15 о возврате 52000 рублей по ИИС (заявление было от 21.08.2018). Сегодня мне на почту приходит письмо с ответом на данное заявление., хотя по закону я должен был получить ответ (если он требовался, например тот же отказ) не позже чем, через 30 дней.

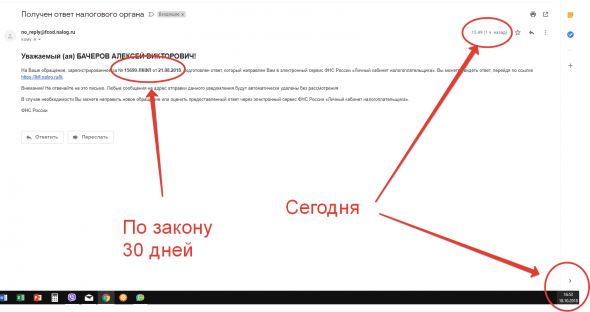
Напомню, что я писал письмо через сервис «Личный кабинет» — 01.10.2018 чтобы налоговая разобралась, что произошлом с моим заявлением от 21.08.2019, поскольку ни ответа не денег я не получил. Ответ на письмо от 01.10.2018 я получил вчера, он датирован 16.10.2018. Скрины приведены в предыдущем посте (https://smart-lab.ru/blog/499854.php). Получается, что ответ на само заявление о возврате я получаю позже, чем на письмо, в котором просил разобраться. Что я могу подумать в этот момент? Там будет примерно та же информация, т.е. год указан неправильно, и поэтому отказ (ровно как и в письме от 16.10.2018).

( Читать дальше )

      Прошлый мой пост я так понял не все поняли. Я чуть расшифрую и немного продолжу.
Вот я привел кол-во регистраций по годам. Цифра практически константа, то есть стабильно ~5500 человек

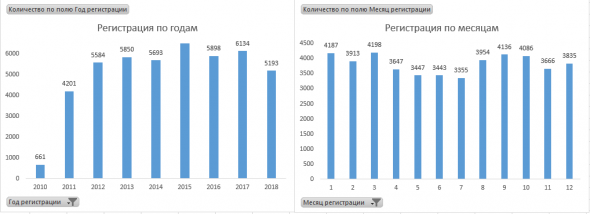
А вот я привел кол-во активных профилей на текущий месяц. Их получилось в районе 16%. То есть порядка 8000 профилей.


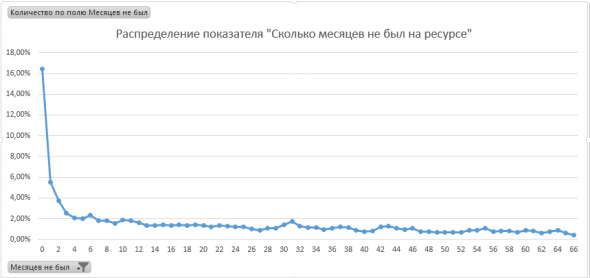
( Читать дальше )

Печальная тенденция, Смарт Лаб резко сливается, в боковике пытаются поймать тренд и лудомания процветает.

Общий минус резко вырос до 2,8 мио(    (похоже большинство хочет расти и рука не поднимается прикрыть минус)

«не за то батька сына драл, что играл, а за то что отыгрывался»


Убыток дня не стоит пытаться отбить быстро, не уходите от своей системы, каждый день не может быть в ПЛЮС.

Убытки системы можно закрыть системно, а вот убыток от сделок вне системы можно и не закрыть вовсе.

Для чего придерживаться убыточного стиля торговли, если это приносит такие минуса на таком коротком отрезке времени? Зачем?! Банальная лудомания?



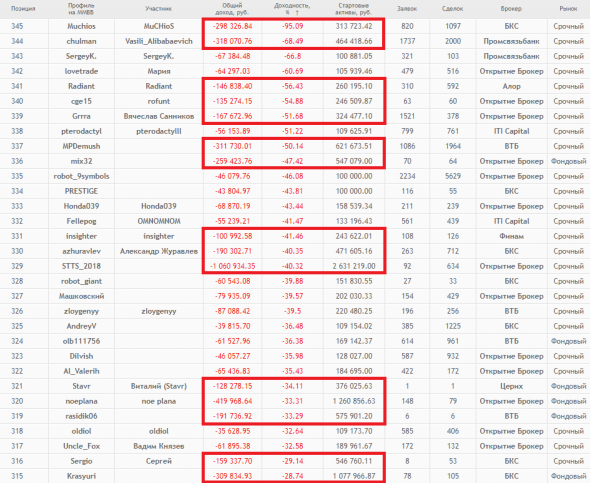
Я ещё с трудом могу понять, когда человек решил ради ЛЧИ сжечь 100 тыр, но 250 и более?! Для чего?

Ну, отдайте бабло в хороший благотворительный фонд со строгой отчетностью?! Нет?!

наткнулся на статью, посчитал будет интересной для прочтения:

Прихожу я сегодня такая классная в Сбербанк, а там милая барышня так воодушевленно мне:

— Давайте мы Вам защиту от мошенников подключим? На все счета, все карты, вообще на все, устанавливается на год, стоит 1 161 руб. в год. Давайте? Отличная штука!

 

Пауза. Она улыбчиво и пристально на меня смотрит, с нетерпением ожидая положительный ответ. В связи с нынешней неповоротливостью моей шеи у меня поднялась только бровь, и все мое недоумение вдруг оказалось на моем лице. Закипание началось, но физическая ограниченность сдерживала эмоциональный напор:

— То есть Вы, как банк, не в состоянии в рамках своей обычной хозяйственной, лицензируемой деятельности и в соответствии с требованиями, предъявляемыми к банкам, обеспечить безопасность моих денег, операций и предлагаете мне эту безопасность за 1 161 руб. в год?

 

А она улыбается и продолжает:

— Ну, это же мошеннические действия, мы-то здесь причём? Мы только операции проводим по счётам, а от мошенников Вы сами должны защищаться.

( Читать дальше )

Очень неприятная история происходит с нашей налоговой службой. Около года назад я долго воевал с налоговой службой по вопросу числящихся на мне транспортных средств, и соответственно налогов, которые мне необходимо уплатить по ним. После моих заявлений, ТС исчезали, потом появлялись другие (более старые) приходилось писать снова и так далее. «Борьба» шла около ГОДА, но в конце концов все пришло в норму. Хорошо, что это был через личный кабинет на www.nalog.ru, потому что если бы это переписка шла по почте, то это бы растянулось на большее время.
Теперь новая напасть. Как владелец иис, я возвращаю 52 000 рублей каждый год по ндфл. Делается это достаточно просто (по идее, и в этом году решили сделать ещё проще вроде как. в прошлом такой проблемы не возникало):
1.Вы сдаете декларацию 3-НДФЛ через тот же личный кабинет.
2.Она проходит камеральную проверку, и налоговый орган выдает решение о возврате (смотри скрин 1).


( Читать дальше )

Всем привет друзья. Летом, я тестировал стратегию барона, нашего, Мюнхгаузена. Итоги можно посмотреть тут: пост

Не так давно я анонсировал второй тест этой стратегии на промежуточных дивидендах. Анонс тут: пост

На сегодняшний день все необходимые позиции набраны, либо при невозможности войти в шорт, сделаны пометки, но продолжаю позиции отслеживать.

Очень скоро презентую итоги второго теста стратегии. Напомню, что тестирую я только на реальных счетах, реальными деньгами. Примерная сумма входа 100 000 руб на акцию.

P.S. Опасно для депозита, не повторять до положительных результатов.

Если понравился материал, подписывайтесь на мой профиль, ставьте плюсы и следите за тестированием новых стратегий. Пока, пока.

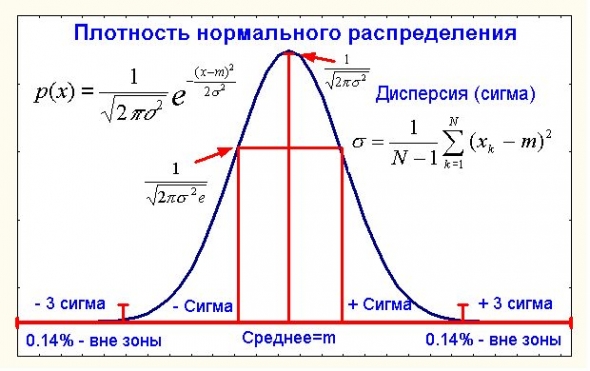
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )