Взято из https://nakhusha.livejournal.com/47609.html

Этот пост будет отдушиной для спекулянтов.

Компания Newfound Research занимается исследованием рыночных моделей.

У них я нашел завлекающую картинку на трендследящую стратегию.



Подробнее о ней вы можете прочесть здесь.

Дьявол, как всегда, кроется в деталях. А именно, какую «машку» выбрать в качестве индикатора. В немного другой статье авторы показывают, каким мог бы быть выход из кризиса 1929 года, используя 6-12 мес. скользящие средние. И результаты весьма разнообразны: от -25% до 136%.



( Читать дальше )

Кому интересно… как менялась за годы доля бумаги в общем обороте на мосбирже.
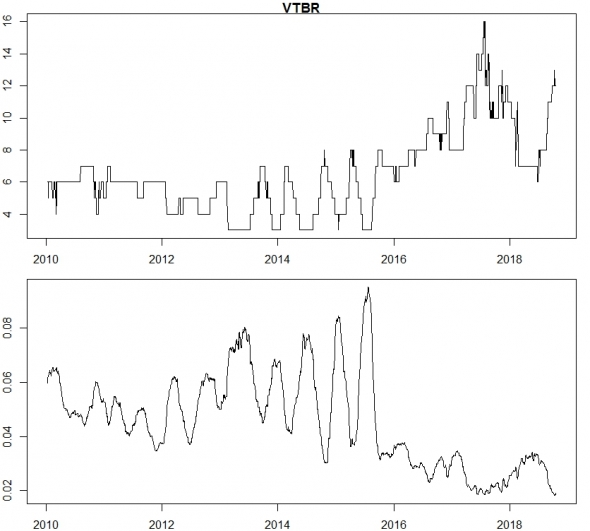
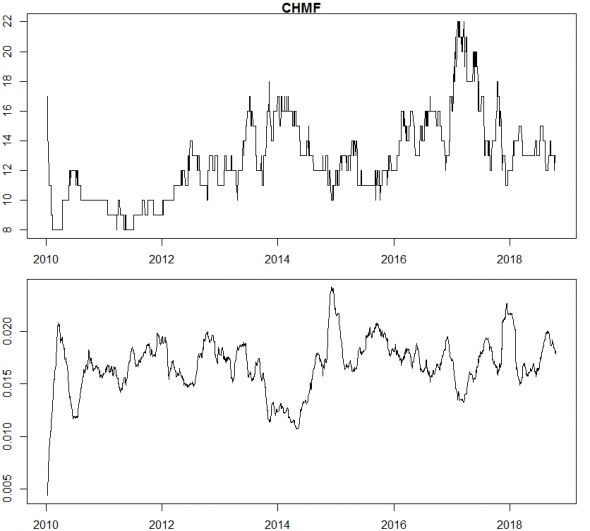
Верхний график это место бумаги в топе по обороту.
Нижний график это доля оборота бумаги от суммарного оборота всех бумаг.
Расчеты сделаны скользящим окном 60 дней.





































( Читать дальше )

Оптимальное количество бумаг в портфеле

         
          Очень часто, когда заходит речь о диверсификации, на лице слушателя появляется скептическая улыбка. Казалось бы, что тут можно придумать нового: все уже давным-давно известно, писано и переписано тысячами трейдеров. Если вкратце резюмировать суть большинства рассуждений на тему диверсификации, то можно выделить две основные идеи:

1. Диверсификация необходима.
2. Избыточная диверсификация неэффективна, ибо не позволяет много заработать.

         Не знаю как вас, а меня всегда интересовал вопрос: каким же должно быть оптимальное количество различных бумаг в портфеле? Интуитивно кажется понятным, что если все деньги поставить на одну бумагу, то риск будет очень велик, и подобная торговля уже сильно смахивает на лотерею (угадал/не угадал). С другой стороны, если купить акции около 100 различных компаний, то, помимо проблем с управлением и анализом такого большого портфеля, рассчитывать на приличную доходность тоже можно с большой натяжкой. Как же быть? Сколько бумаг покупать? Прежде чем дать свой ответ на этот вопрос, мне кажется необходимым сделать небольшую оговорку: я вполне отдаю себе отчет, что каждый раз бывает по-разному, иногда портфель, сформированный из всего 2 бумаг, обгонит портфель из 10 бумаг, а когда-то будет наоборот. Тем не менее, мне хотелось бы провести исследование на статистических данных для ответа на вопрос, какое же число бумаг будет оптимальным наиболее часто или даже точнее будет сказать так: какой интервал бумаг (от и до, например от 6 до 10, или от 10 до 15 и т.д.) обеспечит наибольшую доходность.

( Читать дальше )

      Прошлый мой пост я так понял не все поняли. Я чуть расшифрую и немного продолжу.
Вот я привел кол-во регистраций по годам. Цифра практически константа, то есть стабильно ~5500 человек

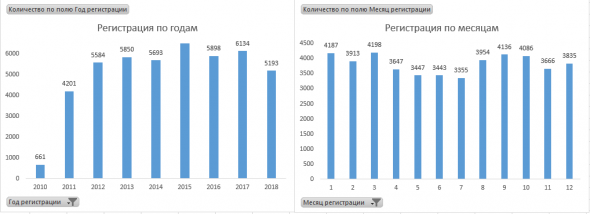
А вот я привел кол-во активных профилей на текущий месяц. Их получилось в районе 16%. То есть порядка 8000 профилей.


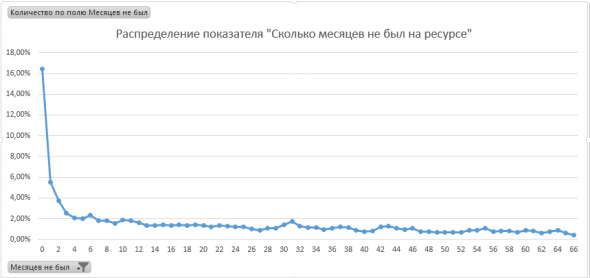
( Читать дальше )

          В своей предыдущей статье “Как обогнать индекс” https://smart-lab.ru/blog/499362.php я привел пример выигрышной торговой стратегии, в данной же статье мне бы хотелось привести пример одной из стратегий, которая практически гарантированно способна проиграть индексу акций в длительной перспективе. У читателя может возникнуть закономерный вопрос, а зачем вообще изучать такую стратегию? Вполне очевидно, что каждый из нас способен придумать бесчисленное множество проигрышных стратегий, ведь основная проблема найти именно тот метод, который позволит заработать на рынке, а для того, чтобы терять деньги много ума не надо, процесс потери денег протекает легко и не требует каких-либо усилий со стороны новичка. И, тем не менее, чтобы избежать очень распространенных в трейдерской среде ошибок, я и написал эту статью.

         Если вы не первый год торгуете на фондовом рынке, то наверняка заметили, что из года в год одни и те же бумаги растут лучше рынка, а другие толкутся на месте или даже падают из года в год. Отличным примером являются Роснефть и Газпром. Для меня торговля на фондовом рынке началась с покупки акций Роснефти на IPO в июне 2006 года. Тогда Газпром стоил дороже Роснефти. С тех пор Роснефть выросла более чем в 2 раза, а Газпром более чем в 2 раза упал. Подобных примеров можно привести много. Отсюда возникает следующая гипотеза: индексу акций можно проиграть, если покупать только худшие бумаги, т.е. те, которые продемонстрировали наименьший рост (или наибольшее падение) за определенный предшествующий текущей дате период. Совершенно очевидно, что доказать строго математически подобную гипотезу невозможно, но мы можем провести тестирование подобной стратегии на исторических данных.

( Читать дальше )

Как и обещал в комментарии из моего предыдущего топика 

smart-lab.ru/blog/499678.php#comment8969912

Исходные данные: закрытия дня с 07.12.2005 по 16.10.2018 для S&P500 и индекса Мосбиржи

VAR00003, если VAR00004=0: центрированные и нормированные приращения логарифмов индекса Мосбиржи
VAR00003, если VAR00004=1: центрированные и нормированные приращения логарифмов индекса S&P500

Результат



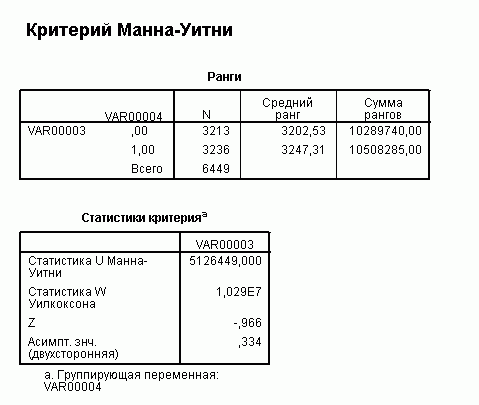
Итого: вероятность ошибиться, утверждая, что эти распределения разные, больше 0,334.

И вывод: выборочные распределения приращений логарифмов дневных значений индексов Мосбиржи и S&P500, вероятней всего, совпадают  с точностью до среднего и дисперсии.

Добрый день.

 
Долго думал, описывать ли свои защитные действия. Решил, так как портфель публичный, то и все позиции должны быть описаны.

Последние сделки перед падением я сделал 5 октября, в пятницу https://smart-lab.ru/blog/497939.php .

 

8 октября, в понедельник, мой портфель был из 12 проданных и 8 купленных путов.

Т.к. я продаю каждую неделю месячный контракт, то примерно у меня портфель состоит из 4 позиций (примерно 4 недели в месяце).

 

10 октября, в среду, при сильном обвале, я откупил последнюю и предпоследнюю недели в профит.

Портфель стал выглядеть так, 6 проданных, 8 купленных контрактов.

 

11 октября, в четверг, утром (1:30 по МСК), я каждые два контракта роллировал в один, уходя на две недели вперед.

Портфель стал выглядеть так, 3 проданных, 8 купленных контрактов.

 

( Читать дальше )

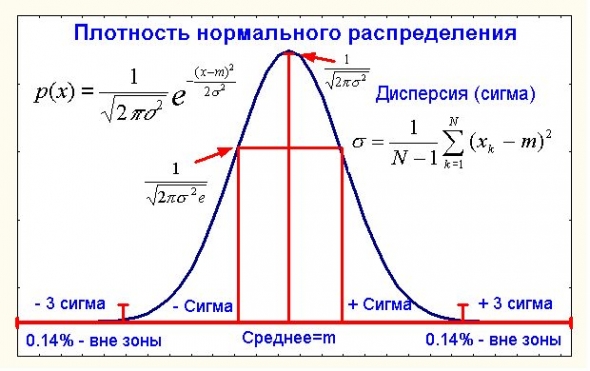
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

 Мы составили список ссылок на лучшие сайты для анализа и подбора облигаций на каждый день
 На практике потребности в анализе облигаций сводятся к 4 основным направлениям:

1. Котировки и графики
2. Новости рынка облигаций
3. Анализ и сравнение
4. Прогнозы и рекомендации

 1. Котировки и графики

 Прежде всего из биржевых котировок нужно уяснить 2 главные вещи:

• какую доходность в процентах годовых вы получите от владения облигацией
• по какой цене в процентах от номинальной стоимости вы её сможете продать

 Список лучших сайтов следующий:

 Smart-lab — котировки ОФЗ (вместе с датами погашения, дюрацией, купонного дохода и фильтрами представлены графики)

 Московская биржа

( Читать дальше )

Как обогнать индекс (пример выигрышной торговой стратегии)

          В кругу экономистов бытует мнение, что обогнать фондовый индекс на длительной перспективе невозможно, и если вам удалось в какой-то определенный год вырваться вперед, получив прибыль гораздо выше той, которую продемонстрировал индекс акций, то в будущем неизбежно ваши результаты не превзойдут индекс, а могут оказаться только хуже него. Подобная точка зрения следует из гипотезы эффективного рынка. К сожалению, экономика отличается от математики тем, что строгое доказательство практически любого утверждения представляется невозможной задачей. Тем не менее, в данной статье мне бы хотелось привести пример одной из стратегий, которая способна обогнать индекс акций в длительной перспективе. Разумеется, я отдаю себе отчет в том, что не могу доказать это математически. Впрочем, в экономике практически везде используются различные гипотезы, которые невозможно доказать, например, почему-то принято  считать, что движение цен подчиняется нормальному распределению, и я что-то нигде не встречал какого-либо доказательства подобного утверждения. Тем не менее, именно на основе гипотезы о нормальном распределении была придумана знаменитая формула Блэка-Шоулза для оценки стоимости опционов, за которую ее авторы даже получили нобелевскую премию.

( Читать дальше )