Добрый день!

Налоговая инспекция утвердила новую форму налоговой декларации 3-НДФЛ за 2018 год. Основание: приказ ФНС России от 03.10.2018 г. № ММВ-7-11/569@. Сам приказ пока не вступил в силу (начало действия документа – 1 января 2019 года). Скачать новую форму декларации можно будет позже.

Почему я обращаю внимание на этот документ? По завершении текущего 2018 года многие из вас будут обязаны отчитаться по полученным доходам, а кто-то будет претендовать на налоговый вычет. Давайте перечислим все возможные случаи, когда подается декларация 3-НДФЛ:
– получение дохода, из которого не был удержан налог налоговым агентом;
– получение дохода из-за рубежа;
– получение дохода от продажи имущества, находящегося в собственности менее трех лет;
– получение выигрыша;
– получение в подарок имущества не от близких родственников;
– необходимость получения налогового вычета в связи с расходами на приобретение или строительство жилья;
– необходимость получения налогового вычета в связи с расходами на лечение;

( Читать дальше )

Доброго воскресного вечера, друзья.

Я хотя здесь и редкий гость, но в торговле уже с 2009 года… К сожалению, мой скромный женский мозг дал возможность получать прибыль не так давно. Я не могла понять в чем проблема. Сначала было изучение рынка, наблюдение за характером его движением и пр. Я много читала, общалась, тестировала, торговала. У меня даже была депрессия от того, что ничего не получалось. Я ни разу не сливала разом депозит, но делала это медленно. Деньги с каждым трейдом стекали как растаявшее мороженое.

Через несколько лет пришла эйфория от прибыли. Благодаря которой я снова начала терять деньги при условии отсутствия другого дополнительного дохода. Сняв почти все, я ушла с рынка. 
Вернувшись, моя торговля почему-то стала другой. Я успокоилась. Ушла с внутридневной торговли на старшие таймфремы. Я больше не пользуюсь стопами, так как всегда знаю цели и возможные риски в каждой сделке. Мне несложно признать неправильность позиции и закрыть ее легко, без судорожных нажиманий на кнопки. Торговля стала какой-то… свободной что ли…

( Читать дальше )

Коллеги, всем добра! Напоминаю, нами проводился мини-конкурс «Мозговой штурм», ссылка на исходник: https://smart-lab.ru/blog/499050.php. Целью конкурса было показать, каким же заковыристым может стать профиль опционных позиций в результате управления в течение торгового периода. Ну и доказать, что трейдер, разбирающийся в опционной торговле, в состоянии решить обратную задачу и восстановить начальный профиль позиции при практически минимальных исходных данных, просто просчитывая логику действий. Напоминаю, что победителем конкурса стал камрад Олег Ложкин, который и добавил в свою смартлабовскую копилку честно заработанные 520 ТМ. Ну, и как обещал – выкладываю всю раскладку по трансформации изначального профиля в конкурсный и его дальнейшее управление с выходом на месячную экспирацию, с традиционной выкладкой скринов окошек используемого ПО  для лучшей визуализации. Для торговли, моделирования и визуализации  использовался классический Квик в связке с  лицензионной программой Option Workshop. Если что-то непонятно по скринам и работе программы – спрашивайте, единственное примечание для ориентирования – красный шарик на профиле в Воркшопе это текущее значение БА.

( Читать дальше )

Продолжение, начало: Торговая стратегия ч. 1

В общем случае необходимо признать, что точно прогнозировать движение цен невозможно. Котировки зависят от сделок множества участников рынка и предсказать конкретное движение в данный момент можно только случайно. Аналогично, не представляется возможным точно определить момент разворота тренда в том или ином инструменте, хотя по объёму торгов и некоторым фигурам теханализа можно сделать вывод, например, об окончании сильного медвежьего или бычьего тренда.

Взяв эти умозаключения за принципы работы на рынке, я решил начинать открытие длинных позиций с малой лотажности. Логика действия следующая: покупаем 100 акций выбранной компании и смотрим на динамику цены. Если цена идёт в нашу сторону, то в соответствии с первым правилом лонговая позиция вверх никогда не усредняется, а подыскивается другой инструмент для набора позиции. Говоря проще, «пирамидинг» по ап-тренду полностью исключён. Если цена идёт против нас, то продолжается набор позиции, средняя начинает движение вниз вслед за «медвежьим» трендом. Наиболее комфортны низкие цены, в диапазоне $5-$20 за акцию. Здесь с психологической точки зрения важно соотношение прибыль/убыток: маловероятно, что крупная компания будет торговаться около 0, и даже если цена уйдёт значительно ниже, изначальная ставка была небольшой и мы теряем немного. Если же случится разворот, то возможны два варианта: либо мы заработаем немного, не успев набрать достаточную позу, либо в процессе усреднения наберём достаточный объём к моменту, когда в инструменте начнётся бычий тренд и наша прибыль будет значительной. Этот метод называется

( Читать дальше )

Есть ли смысл покупать торговых роботов? — Нет.

На этом, в принципе, можно было бы и закончить пост. Но расшифрую.

 Для обоснования буду использовать модель воронки, сознательно не буду использовать никаких цифр, если интересно — сами подставьте. Просто не люблю писать проценты и вероятности от балды, лучше ничего не писать, чем такое.

 Итак, погнали. На рынке имеется некоторое кол-во торговых роботов, которых можно приобрести, а теперь давайте прикинем, велики ли шансы заработать на этом мероприятии (на покупке, не на продаже :))) ). Далее идут этапы/слои/фильтры, отсеивающие роботов, которые не позволили бы вам заработать:

  — Часть предложений — мошеннические (тут как везде, где есть хоть какие-то деньги — есть мошенники — возможно, при покупке вам даже ничего не пришлют).

— После отсеивания мошенников, часть товарищей продают заведомо неприбильных роботов (ими движет мотивации типа: а. он когда-то работал, мне трудно смириться с тем, что он больше не работаю, выжму из него ещё немного, продавая его; б. я протестировал на 150 инструментах, на 27 таймфреймах, на 5-ти комбинациях таймфрейм-инструмент робото зарабатывал — а-чё, не плюсовой, скажете? в. главное, красиво обставить продажу и чтоб купили, дальше хоть трава не расти, пох, что он минусовой).

( Читать дальше )

Комментарий А.Г. в одном из постов:
  Вы явно не знаете, что средняя цена нефти в 70-х была 50$  и это были совсем другие доллары «по весу», а до 25$  нефть упала при Андропове   и плюс-минус 5$ оставалась до 1991-го. А добыча СССР  была больше, так как были и Казахстан и Азербайджан.  И вообще советскую добычу РСФСР, Россия превзошла только после кризиса 2008-го.

А.Г. как всегда намешал с цифрами, правду с домыслами. Посмотрим реальность. Добыча была сопоставима, но не больше, причем экспорт был меньше. И на нефтяную иглу потихонечку мы начали подсаживаться после смерти Сталина:

Про покупательную способность, которая судя по следующему его комментарию, в СССР была меньше, я даже не буду давать картинки, чтобы никого не расстраивать. Скажу лишь, что по продуктам она была в разы, а то и в десятки раз выше. И заметьте, у жителей СССР не было многих трат сегодняшних россиян — например, ипотеки.

( Читать дальше )

По просьбе коллег с этого сайта излагаю свою историю покупки робота.

Три года назад была у меня идея зарабатывать на бирже с помощью роботов. Зная, что на этом рынке полно мошенников, начал искать наиболее надежные варианты. Более всего мне понравился сайт КБробота (в миру Евгений Черных).

Из всех предложенных на сайте вариантов больше всего понравился робот «опционный перехватчик», потому что там была статья «Как я стал миллионером», где Евгений подробно свой путь к миллиону с помощью этого робота. Звучало очень убедительно. Еще подкупила куча положительных отзавов на сайте Евгения.

Цена была небольшая и 10т.р. улетели на карту Евгения.

Немного поковырявшись с запуском, установил робота на отдельный компьютер, дал ему один лот и начал ждать чуда. Чуда не произошло. Если по заверениям роботорговца, робот должен был работать каждый день в небольшой плюс, то у меня робот работал каждый день в стабильный минус.

Я начал отслеживать все сделки и обнаружил, что робот пропустил одну прибыльную сделку, обратился в «службу поддержки», где получил ответ — «такого не может быть»

( Читать дальше )

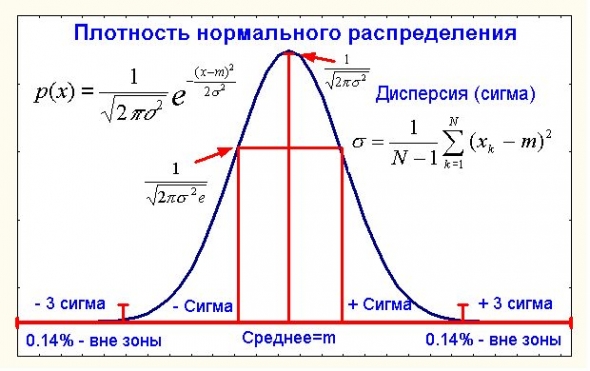
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Давно известно, что если вы хотите купить какую-то акцию дешевле — продайте на нее пут не в деньгах. Например хотите сбер по 180? Продайте 180й пут. Если цена упадет ниже 180 — то вы получите акцию по 180 и еще премию по путу. (например 2) и таким образом эффективная цена покупки будет 178. Ну, а если цена не упала — то получите просто истекшую премию в размере 2, что в пересчете на ГО довольно неплохая доходность. Пример выше — условный, надо смотреть на цены, страйки, волатильность. Но есть одно простое правило — путы лучше продавать тогда, когда рынок уже припал и вола подскочила и часть падения уже пройдена. (Так, сейчас кто-то бросится писать коммент про мой 2008й год. Да, такое бывает. Но сейчас этих предпосылок, вроде как, нет).
Чем еще хорошо продавать путы? что если акция болтается в диапазоне, то вы собираете премию. Обычный владелец стока при неизменной (почти) цене акции получит лишь дивиденды, а вы — опционную премию. (правда не будет дивидендов)

Но тут возникает два момента — первый, с опционами не все знакомы и не все связываются и второй — не на каждый инструмент есть опцион. Поэтому сейчас я расскажу стратегию торговли, для которой не нужны опционы, но суть ее особо не поменяется. Более того, добавятся дивиденды.

( Читать дальше )