Дневные левый 3, правый 3.7.
Месячные левый 3, правый 5.2 (но я думаю он тоже 3.7, просто данных меньше и его не видно).

Это значит SkewStudentT(𝜇,𝜎,𝜈,𝜆) может быть не достаточно, если мы зафиксируем nu=3, это переоценит вероятность редких положит событий, и хотя сама по себе ошибка может быть малой, тот факт что это экстремальное событие большого масштаба, да еще и в экспоненте exp(log r) увеличит ошибку.

В идеале конечно надо что то типа SkewStudentT(𝜇,𝜎,𝜈𝑙,𝜈𝑟,𝜆) с разными хвостами, но таких вроде как нет.

Либо, зафиксировать nu=3.7, это недооценит убытки, но зато ошибка не будет увеличиваться большим масштабом события.

Добавлено:

Ошибка (относителная) для VaR, портфель из 10 акций и события раз в 10 лет, при хвосте 3 и 3.7. Дневные: ~1.22 раза, месячные: ~1.24 раза. Вполне ощутимая разница.

# Daily, typical daily log returns StudentT(0.001, 0.015)
p = 1-1/(365*10*10) # once in 10y for portfolio of 10 stocks
exp(
  quantile(StudentT(0.001, 0.015, 3), p) - 
  quantile(StudentT(0.001, 0.015, 3.7), p)
) # => 1.22

# Monthly, typical monthly log returns StudentT(0.01, 0.08)
p = 1-1/(12*10*10) # once in 10y for portfolio of 10 stocks
exp(
  quantile(StudentT(0.01, 0.08, 3), p) - 
  quantile(StudentT(0.01, 0.08, 3.7), p)
) # => 1.24

Для лог доходности акций r = log S_T/S_0 степень хвоста не зависит от периода, прибыль за день, месяц или год.

Это видно математически Pr(X>x) ~ Cx^-a — степень a сохраняется при агрегировании (суммировании), меняется лишь константа.

И на графиках log log правого хвоста > 0.97 квантили, цвет дециль волатильности (множественные линии одного цвета — когорты чтобы избежать overlapping bias). Наклон на всех периодах одинаковый.

Недавно потребовалось установить экспоненту Парето хвоста распределения вероятностей. И чтобы посмотреть насколько хорошо методы EVT работают, я сделал простой пример.
Пример: 30 сэмплов StudentT(df=4), каждый размером 20000. Определить экспоненту хвоста используя методы: Хилла, GPD, LeastSquares, CDF LogLog PLot.
Результаты ужасны: точность всех методов плюс минус километр. Я не вижу ни малейшего смысла в EVT поскольку вручную по линейке установить наклон линии на ЛогЛог Графике CDF оказывается не хуже (мне кажется даже лучше) чем специализированные методы EVT.
На графике — y — найденная экспонента хвоста, каждая линия это отдельный сэмпл, цвет метод определения, х — гиперпараметр (число точек в хвосте распределения которые использовались в расчетах). Верный результат это горизонтальная линия y=4, вместо этого мы наблюдаем, в зависимости от метода — систематические ошибки, либо дикий хаос.


Даже, мне кажется с линейкой предпочтительней, график лог лог. Поскольку ты боль менее визуально и интуитивно понимаешь что делаешь. 

( Читать дальше )

Много методов: Hill, EVT GPT, регрессия. И все с точностью километр. На графике — 30 симуляций: 30 сэмплов StudentT(df=4) 20к, для каждого сэмпла определяется df различным эстиматором (цвет линии), ось х — значение трешхолда эстиматора. 


Правильный результат — постоянная линия с y=4. Единственный нормальный результат (красные линии) это MLE полного распределения, но это именно что эстиматор полного распределение, а не Tail Estimator. Среди хвостовых эстиматоров ни одного хорошего.

EVT GPT на который я больше всего расчитывал (синии линии), вообще ничего не измеряет (но возможно я допустил ошибку и неверно его считаю, по идее он должен быть самый точный).

Подробней www.reddit.com/r/nassimtaleb/comments/1mdwqjw/huge_errors_in_heavy_tail_estimators_hill_evt_gpt/
Код gist.github.com/al6x/11e66ab92c525f2ef2c1510e6ac7a3f7

Получается неверный результат если есть ассиметричность, настоящее значение 4, но он неверно определяет как 3 для левого и 5 дле правого хвоста. Или, скорей дело не в Hill а само распределение искажает хвосты? Никто не сталкивался? код



На графике две линии должны стабилизироваться на отметке 4, а они показывают 3 и 5.

Я нашел то что искал. Распределение а) способное с достаточной точностью аппроксимировать Эмпирическое Распределение цен на диапазонах 180, 360, 720 дней б) имеющее достаточно простую форму в) с возможностью маштабировать.

Ассиметричный Гауссовской Микс из 3х компонент, отдельно для Положительных и Отрицательных изменений, с Фиксированными Нулевыми Средними. Это 8 параметров, но два из них определяются оч точно и требуют мизера данных, поэтому их можно не учитывать, остается 6 параметров, 6 сигм. Это много, но фиттинг будет на десятках лет так что данных достаточно.

Финальная подстройка — сжать/растянуть полученную модель на текущую волатильность, будет по 1-2 параметрам.

На графиках, зеленый положит изменения цен, красный отрицательные. Яркие цвета — эмпирическое, зеленый красный полутон Гауссовский Микс, бирюзовый/розовый полутона — Обобщенное Гиперболическое (добавил чисто для сравнения, оно приближает хуже и непредсказуемо, причем самую важную часть — хвост).




( Читать дальше )

Апроксимация изменений цен Гауссовским Миксом, отдельно для положительных и отрицательных изменений.

Благодарность Михаилу, что поправил алгоритм фиттинга модели для Гауссовского Микса.

Микрософт, 360 дней, зеленая положительные изменения, красная — отрицательные. Слабозеленая/слабокрасная гауссовский микс. Почти невидимая зеленая/красная — обычное гауусовское распредление.

Для каждого случая два графика, графики одинаковы и показывают P(X > x) (комплементарная CDF), но в разных масштабах, логарифмическом и линейном, на одном лучше видна голова на другом хвост.



Микрософт 180 дней



( Читать дальше )

Продолжаю сравнивать распределения изменения цены, логарифмы, отцентрированые пo среднему, для 360 и 30 дней, отдельно графики положительных изменений (зеленые) и отрицательных (красные). Сравнение с нормальным (полупрозрачные зеленые и красные линии), как видно — не совпадает, и ассиметрия также заметна.

Микрософт, 360 дней


Микрософт, 30 дней



( Читать дальше )

Увидел сегодня, компактно в двух строчках целая куча концепций.

Я рассчитал распределение изменений цены акций (дифф). Имеются ввиду мультипликативны изменения (diff), во сколько раз меняется цена акции за каждый день, d(t) = p(t) / p(t-1)

Насколько я знаю, распределение должно выглядеть как распределение по Power law (распределение Парето). С CDF, являющейся линией на графике log-log.

Но CDF который я получил не похож на линию на графике log-log. Почему?

Mожет ли это быть вызвано тем, что распределение имеет два хвоста вместо одного? Поскольку имеются два редких событий: редкие огромные ежедневные падения цен с d <0,7 и редкие огромные ежедневные повышения цен d > 1,4

Насколько мне известно, линейный тест распределения парето на логлог графике используется для распределений с одним хвостом. Как например распределение богатства у людей. Можно ли его также использовать для распределения с двумя хвостами?

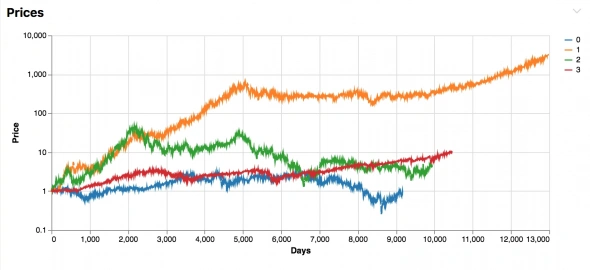
Пример

Ежедневные цены на 4 акции за пару лет, нормированные на 1 за первый день.

( Читать дальше )