Практическая польза от Теории Экстремальных Значений? EVT

Недавно потребовалось установить экспоненту Парето хвоста распределения вероятностей. И чтобы посмотреть насколько хорошо методы EVT работают, я сделал простой пример.
Пример: 30 сэмплов StudentT(df=4), каждый размером 20000. Определить экспоненту хвоста используя методы: Хилла, GPD, LeastSquares, CDF LogLog PLot.
Результаты ужасны: точность всех методов плюс минус километр. Я не вижу ни малейшего смысла в EVT поскольку вручную по линейке установить наклон линии на ЛогЛог Графике CDF оказывается не хуже (мне кажется даже лучше) чем специализированные методы EVT.
На графике — y — найденная экспонента хвоста, каждая линия это отдельный сэмпл, цвет метод определения, х — гиперпараметр (число точек в хвосте распределения которые использовались в расчетах). Верный результат это горизонтальная линия y=4, вместо этого мы наблюдаем, в зависимости от метода — систематические ошибки, либо дикий хаос.


Даже, мне кажется с линейкой предпочтительней, график лог лог. Поскольку ты боль менее визуально и интуитивно понимаешь что делаешь. 



А когда ты ищешь на графике Хила «участок когда график стабилизировался» — ну и как его там найти (см картинку ниже, черные линии)? Выбирай любой кусок графика который нравится (отмечены желтым кружком), от экспоненты 3 до 4 — и на любом значении этого интервала график Хила выглядит «стабильный», выбирай любое значение которое нравится. И получается смысл тогда в этом методе Хила? Я и с линейкой на лог лог графике установлю что экспонента где то между 3 и 4, и при этом еще осмысленно будет видно что это значит, чем абстрактно выискывать некий стабильный участок на графике Хилла.


Ну а GPT (Peak over Treschold) — это MLE фиттинг хвоста, и это должен быть самый точный метод. А он дает наихудший результат из всех, полный хаос, определяя экспоненту хвоста от 2 до 8, причем совершенно нестабильный и дико прыгает, малейшее изменение гиперпараметров и вместо результата 3 получаешь 6 — это как вообще?


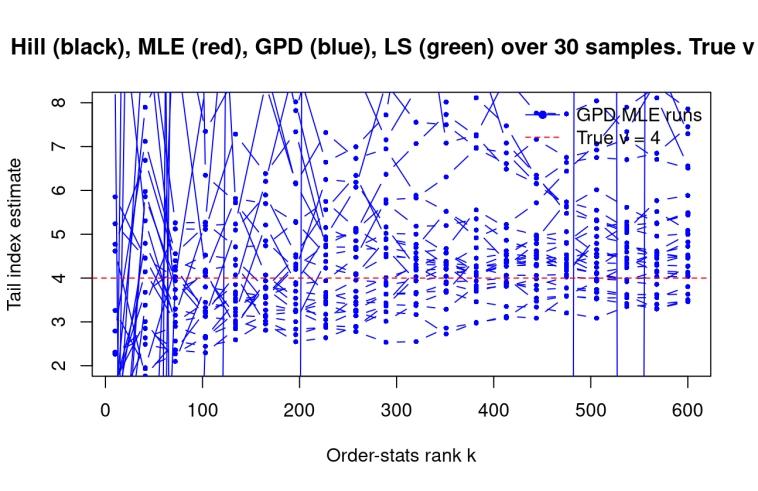
Наилучший резульат дал MLE фиттинг полного распределения StudentT (красные линии на первом графике). Но, это не в счет. Потому что здесь простой пример, где распределение симметрично, и мы точно знаем что это StudentT, это не будет также хорошо работать в реальности, если распределение перекошено например и имеет разные экспоненты левого и правого хвостов. Поэтому красные линии, они не считаются.
Вывод:

Я не понимаю какой смысл в EVT если она дает такие результаты? Получается лог лог график и линейка — проще, наглядне, надежней и даже точнее? Есть еще пара методов Pickands Estimator который вроде чуть лучше чем Hill но уже влом смотреть, едва ли там сильно лучше.
Код расчетов на Python и R quant.stackexchange.com/questions/83839/evt-how-to-estimate-tail-exponent-with-good-precision-hill-gpt-evt-leastsqu