Блог им. AlexeyPetrushin
Почему дневные изменения цен акций не следуют Распределению Парето?
- 20 сентября 2021, 23:10
- |
Я рассчитал распределение изменений цены акций (дифф). Имеются ввиду мультипликативны изменения (diff), во сколько раз меняется цена акции за каждый день, d(t) = p(t) / p(t-1)
Насколько я знаю, распределение должно выглядеть как распределение по Power law (распределение Парето). С CDF, являющейся линией на графике log-log.
Но CDF который я получил не похож на линию на графике log-log. Почему?
Mожет ли это быть вызвано тем, что распределение имеет два хвоста вместо одного? Поскольку имеются два редких событий: редкие огромные ежедневные падения цен с d <0,7 и редкие огромные ежедневные повышения цен d > 1,4
Насколько мне известно, линейный тест распределения парето на логлог графике используется для распределений с одним хвостом. Как например распределение богатства у людей. Можно ли его также использовать для распределения с двумя хвостами?
Пример
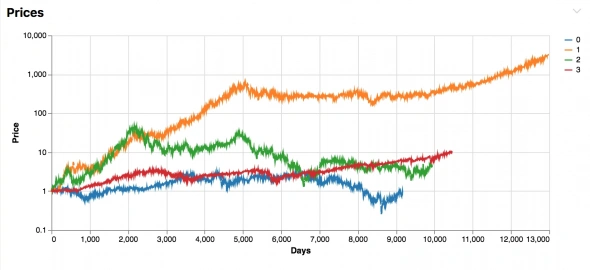
Ежедневные цены на 4 акции за пару лет, нормированные на 1 за первый день.
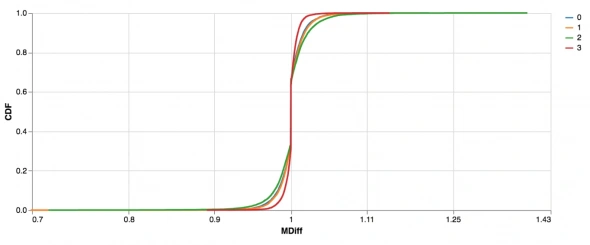
CDF ежедневных различий. Ось x — это логарифмическая шкала, чтобы изменения выглядели симметрично относительно x = 1.
Изобразим его в логарифмическом масштабе, и он получается совсем не похож на линию, ни один хвост, ни другой.
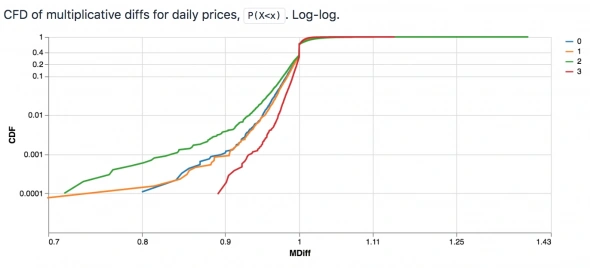
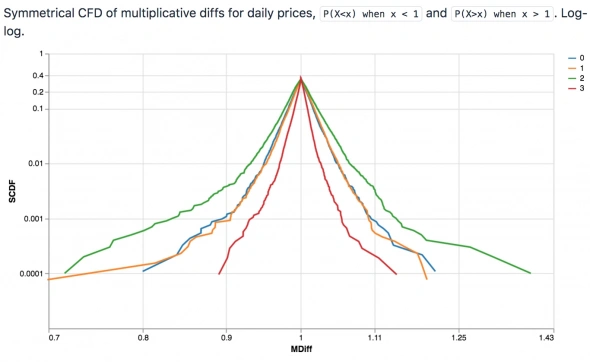
На предыдущей диаграмме один хвост был смят. Поэтому я рассчитал гибридную CDF, два разных CDF, один для d <1, а другой для d> 1, и опять построил его на лог-лог графике, чтобы можно было увидеть оба хвоста. Но проблема осталась, ни левая ни правая части графика не похожи на линию. Почему?
P.S.
Если это не Парето, то что это может быть за распределение?
Апдейт:
Судя по всему это может быть распределение Каучи, оно описывает распределение от соотношения двух случайных величин X1/X2. Плохо что для него не так просто подобрать параметры по данным....
Но думаю есть способ проще, попробую микс из гауссовских моделей.

теги блога Alex Craft
- amd
- CPI
- GARCH
- Implied Volatility
- java
- Javascript
- Matlab
- microsoft
- options
- portfolio
- python
- SV
- swift
- VAR
- volatility
- акции
- алгоритм
- алготрейдинг
- аналитика
- банки
- Беларусь
- Блэк-Шоулз
- Брокер
- брокеры
- визуализация
- волатильность
- данные
- деньги
- доллар
- доллар рубль
- золото
- игра
- ИИ
- иммиграция
- инвестирование
- инвестиции
- инвестиции в недвижимость
- инфляция
- инфляция в России
- инфляция в США
- искусственный интеллект
- исторические данные
- Келли
- макро
- Мандельброт
- математика
- Медицина
- мобильный пост
- модели
- модель
- монте-карло
- мудрость
- Нассим Талеб
- недвижимость
- Нелинейность рынка
- Нефть
- Новости
- оптимальный портфель
- опцион
- опционы
- отчёт
- оффтоп
- парето
- плечи
- политика
- портфолио
- премиальные опционы
- прибыль
- прогноз
- программироание
- пут опцион
- пут опционы
- работа
- распределение
- ресурсы
- риск
- рост
- рубль
- рынки
- рынок
- серебро
- спекуляции
- статистика
- стратегии
- США
- талеб
- теханализ
- технический анализ
- торговые роботы
- торговые сигналы
- трейдинг
- убытки
- уран
- форекс
- фракталы
- фундаментал
- хэдж
- экономика
- экономика США
- энергия





















При изначальной выборке нужно было брать на порядок большее число акций, чтобы снизить значимость случайных событий (инсайд к примеру повлек рост или обвал) на итоговый график.
А почему должно?
Вообще моя цель была увидеть волатильность. Как ее лучше увидеть и измерить (я не хочу использовать нормальное распределение и его измерение волатильности).
Я хотел увидеть как меняется волатильность и распределение во времени.
Но не дошел до этого потому что проблемы начались гораздо раньше, я ожидал увидеть распределение парето, а увидел совсем другое и сейчас осмысливаю увиденное…