математика
Граальное закрытие позы
- 15 февраля 2021, 13:48
- |
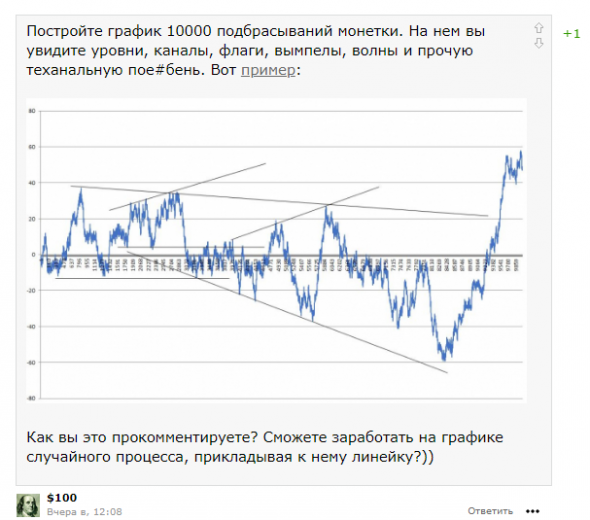
Берем дневки сбера за 10 лет (~2500 свечей) и считаем процент отклонения хая и лоя от предыдущего закрытия. Результаты выглядят так:
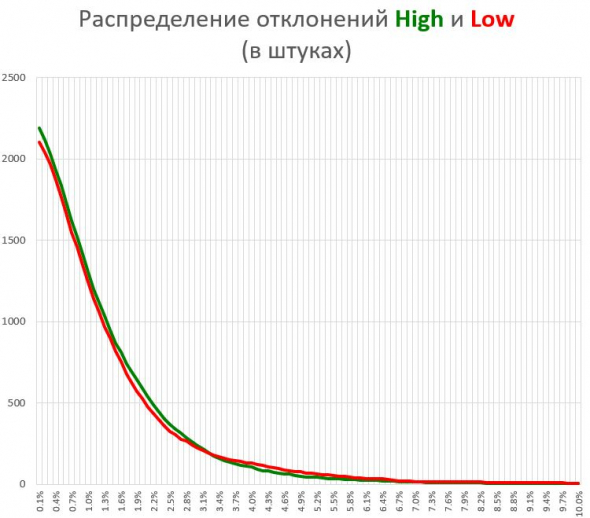
Мы видим:
1000 свечей показали хай и/или лой на уровне 1.3% от предыдущего закрытия.
500 свечей показали хай и/или лой на уровне 2.0% от предыдущего закрытия.
И т.д.
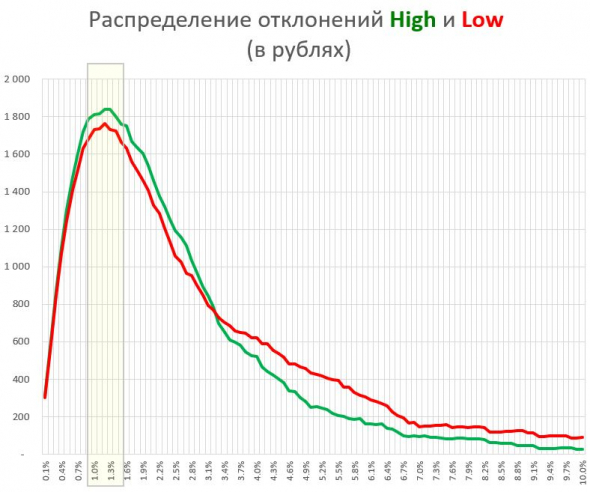
Переведем полученные данные в рубли:
( Читать дальше )
- комментировать
- 5.5К | ★11
- Комментарии ( 28 )
Как выбрать супруга (да и акции) с помощью математики!
- 06 февраля 2021, 14:24
- |
В моем окружении есть мужчины, у которых было больше 100 женщин!!!
Для меня, прожившего почти 20 лет с одной женой, такие цифры кажутся немыслимыми, фантастическими. Скоро и мне после развода предстоит ходить на свидания и возникает вопрос: «Когда остановиться? На сколько свиданий нужно сходить, чтобы выбрать ту единственную?».
Оказывается, что математики тоже люди. И у них стоит аналогичная задача выбрать себе супруга по жизни. И они нашли математическое решение!
Вот инструкция по выбору супруга из книги Мэтта Паркера «Чем заняться в четвертом измерении? Приключения математика в мире бесконечности»:
Шаг 1: Рассчитайте, с каким количеством людей n вы можете сходить на свидание в течение всей жизни.
Шаг 2: Рассчитайте квадратный корень этого числа √n.Шаг 3: Сходите на свидание, а затем отвергните первых √n людей; лучшие из них зададут для вас исходный уровень.
( Читать дальше )
В защиту математиков.
- 31 декабря 2020, 19:02
- |
Сам не математик, хотя в самой профессии кроме математики, пожалуй, ничего и нет. Длительное время занимался мат. моделированием систем, и эта область мне близка как по образованию, так и по роду деятельности.
После ВУЗа работал я в НИИ. Мужики в обед в домино резались, я шахматы, блиц 5 мин предпочитал. В домино не умею и не люблю.
И, вот, зашел к нам как-то в обед математик из соседнего отдела по каким-то делам (вообще, хождение по отделам без надобности не приветствовалось, но какие-то пересечения по делу были). Обеды у отделов в разное время, вот он в обед и попал.
Ребята ему в домино предложили сыграть — у них четвертого не было. Он — да, типа, не умею и т.д. Ладно, объяснили ему как ходят-как сдают, сели. И наш математик их сделал несколько партий подряд, впервые сев играть. Мужики в шоке были.
Как они потом говорили, он им сказал что-то типа — Отложите ваши фишки, а читайте лучше книжки.
Думаю, что и в трейдинге математика далеко не на последнем, если не на первом месте. И сам на рынке работаю исключительно мат методами.
Ах, да, всех с наступающим Новым Годом! Успехов во всех ваших начинаниях.
Тот Самый Грааль
- 14 декабря 2020, 14:22
- |
Использовав числа самой известной математической возвратной последовательности (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377...), российский журналист Сергей Суворов вывел правильную версию истории тысячелетий, столетий, десятилетий и так далее.
Любой временной отрезок — тысячелетие, столетие, десятилетие, год, месяц, неделя, день, час, минута — делится на 3 растущих периода, между которыми небольшие периоды упадка.
Например, каждое тысячелетие делится на следующие временные отрезки в годах:
34 + (144 + 144) + 34 + (144 + 144) + 34 + (144 + 144) + 34 = 1000 лет, где 144 года — периода развития, а 34 года — периоды упадка.
Таким образом правильной версией истории второго тысячелетия является такая:
1034 — 1178 — 1322 — 1356 — 1500 — 1644 — 1678 — 1822 — 1966.
А именно:
1000-1034 — это Кризис начала века;
1034-1178 + 1178-1322 год — это Эпоха Высокого Средневековья;
1322-1356- это Кризис Позднего Средневековья;
1356-1500 + 1500-1644 год — это Эпоха Возрождения;
( Читать дальше )
Субботнее: Решаем олимпиаду для 5ого класса 1 четверть )))
- 17 октября 2020, 12:24
- |
А все ли тут смогут решить задачки для пятиклашек за отведенные полчаса ???

( Читать дальше )
Природа построена не на чисто математической основе...
- 28 августа 2020, 22:20
- |
В математике нет настоящих противоречий.
Гаусс
Логика — это искусство уверенно совершать ошибки (Сливать на бирже)).
Неизвестный автор
https://smart-lab.ru/blog/642215.php
После этого на меня набросился математический планктон с критикой. Лучшим ответом на шипение математического планктона является книга, которая написана Математиком и критикует математику.
К сожалению, уже вначале книги математик Клайн Морис констатирует один существенный факт:
Для получения своих удивительных, мощных результатов математика использовала особый метод — метод дедуктивных выводов из небольшого числа самоочевидных принципов, называемых аксиомами; этот метод знаком каждому школьнику — прежде всего из курса геометрии. Природа дедуктивного вывода такова, что она гарантирует истинность заключения, если только истинны исходные аксиомы. Очевидная, безотказная и безупречная логика дедуктивного вывода позволила математикам извлечь из аксиом многочисленные неоспоримые и неопровержимые заключения. Эту особенность математики многие отмечают и поныне. Всякий раз, когда нужно привести пример надежных и точных умозаключений, ссылаются на математику.
Отсюда напрашивался вывод, что природа построена не на чисто математической основе, а если такая первооснова и существует, то созданная человеком математика не обязательно соответствует ей. Ключ к реальности был утерян. Осознание этой потери было первым из бедствий, обрушившихся на математику.
( Читать дальше )
Математика и трейдинг
- 06 августа 2020, 08:26
- |
Рынок — это не случайное блуждание (хотя графики цен и СБ имеют внешнее сходство). Рынок — это чистая психология. Достаточно открыть вчерашнюю ветку по нефти и сравнить комментарии людей с рыночной динамикой. Ударный день вверх, а люди шортят и усредняются. Понимание того, ПОЧЕМУ ИМЕННО они занимают позиции против рынка и теряют деньги — есть ключ к пониманию рынка в целом.
Знание математики на глубоком уровне не является определяющим условием успеха. Достаточно знания элементарных вычислений и основ теории вероятностей. Гораздо важнее понимать, как будет действовать толпа в определённых ситуациях. Построение торговой системы исключительно на статистической обработке ценовых рядов, без понимания того чьи и почему деньги ты зарабатываешь, как правило, даёт мизерные доходности. Как из-за большой конкуренции (все шерстят одни и те же цифры одними и теми же методами), так и из-за того, что использовать математические методы применительно к рынку, всё равно что использовать топор для резьбы по дереву. Но если других инструментов нет, то, конечно, это лучше, чем лудоманить наугад. Но говорить о том, что сложные математические вычисления — единственный путь к успеху — заблуждение. Трейдинг — не точная наука. Математики стали заметны в трейдинге постольку, поскольку трейдеры сильно измельчали. Сейчас все поголовно ищут Грааль, чтобы закодить его и вытянуть ноги на пуфик (а пока грааля нет, посматривают hh.ru). Но мало кто системно торгует руками «технику» по «старой школе». Потому что для этого скиллы нужны, а люди не любят работать над собой.
Авторегрессия или автокорреляция?
- 20 июля 2020, 16:49
- |
Как называются:
1. Зависимость следующего приращения цены от предыдущего.
2. Зависимость следующего приращения цены от суммы предыдущих.
Трудности формализации сигналов
- 07 июля 2020, 13:43
- |
Допустим, у нас есть задача — формализовать сигнал для ТС.
Например, на слом тренда.
Пробуем это делать и натыкаемся вот на что:
1. Вводим условие: «Растущий тренд считается сломанным, если снижение продолжилось до значения цены = 100».
Здесь возникает затруднение: с точки зрения содержания нет разницы между 99 и 101, но сигналы 99 и 101 робот отработает противоположным образом.
2. Пытаемся усложнить задачу и добавить временное измерение.
Формулируем: «Растущий тренд считается сломанным, если снижение продолжилось до значения цены = 100 и продержалось там время 100».
И снова упираемся в то же самое: с точки зрения содержания нет разницы между временем 99 и временем 101, но сигналы 99 и 101 робот отработает противоположным образом.
3. Пытаемся вырваться из этой западни и вводим плавающие (например, в зависимости от волатильности или ещё какого-нибудь параметра) границы.
Формулируем: «Растущий тренд считается сломанным, если снижение продолжилось до значения цены = „100 * волатильность“ и продержалось там время = „100 * волатильность“.
И снова упираемся в стену, потому что с точки зрения содержания нет разницы между умножением на волатильность 99 или 101, как времени, так и расстояния в пунктах — а сигнал будет получаться противоположный.
Любой чётко закреплённый параметр в расчётах заводит нас в эту западню.
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал