Решил с вашими играми «письками помериться» :))))
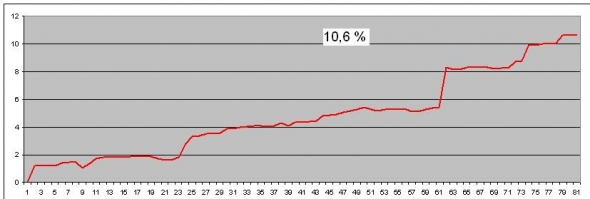
Прирост моего счета за этот период 10,6%

FZF, 
Экономика — это управление вашим гормональным фоном. Иначе бы люди не покупали рваные, поношенные джинсы по цене новых. Монетизируют не пользу и потребности, а вашу глупость.

Да автор вообще не знает элементарных арифметических действий. Результат его «игры» не сумма, а произведение величин 1.5 и 0.6. Чтобы произведение свести к сумме, надо прологарифмировать и получаем, что Ln(1.5) =0.405465, а Ln(0.6)= -0.51083. Таким образом натуральный логарифм накопленного результата «игры» имеет нарастающее отрицательное математическое ожидание -0.05268*n, где n — число испытаний. С какого «будуна» автор говорит о положительном МО?

Автор демонстрирует полное незнание предмета, который критикует. Впрочем отсылка к аналогичной по «знанию» теории вероятностей книге «Одураченные случайностью» уже характеризует автора.

Лисицин, спасибо. У себя такой аномалии не заметил. Прикладываю скрин за последний месяц, там для Ri (серия 19.12) получается примерно -0.02...-0.01 (красная линия — наклон для отрицательных приращений цены, у нее наклон примерно -0.02; зеленая линия — наклон для положительных приращений цены, примерно -0.01).

Единственно, показалось странным, что иногда корреляция mH с приращениями цены была положительная. Т.е. БА наверх, и его вола/подвижность начинает расти. БА вниз — и вола падает. Как будто рынок не верит в рост, и когда фьюч растет — удивляется и начинает слегка бурлить туда-сюда. А когда Ri падает, то типа так и ожидалось, и сползание идет на минимальной воле. Вот это показалось странным: у bk отрицательный наклон, а у bh — положительный.

Кирилл Браулов, с разрешения Курбаковского показываю, как делается сглаживание в той версии модели, которую использую я. Сначала считаются цены call,put с коэффициентом дрейфа bk — C(bk),P(bk). Потом считаются весовые коэффициенты ac=P(bk)/[C(bk)+P(bk)]; ap=C(bk)/[C(bk)+P(bk)].
Далее из коэффициентов bc,bp которые подбираются по рыночным ценам строится средневзвешенное b=bc*ac+bp*ap. Это гладкая функция страйка, на правом хвосте совпадает с bc, на левом — c bp. В центральной точке b=(bc+bp)/2. Этот сглаженный коэффициент используется для расчета цен опционов и всех производных. При этом кривая волатильности (мобильности) становится гладкой и принимает привычный вид.
Но, как я понимаю, это не единственный из возможных методов сглаживания.

Кирилл Браулов, дежавю, я видел почти такую картинку (с поведением bc,bp по времени) у Курбаковского. Он раньше эти закономерности точно учитывал. Изменения касались расчета теты — чем ближе экспирация, тем медленнее дешевеют хвосты. Но потом он вроде решил, что это слишком усложняет модель и правильнее не торговать хвостами. Попробую расспросить его подробнее.
Что касается доходности — у меня норма 30 годовых в валюте. У него, наверное, больше

Кирилл Браулов, Выбрал некие цены базового актива, волатильность, безрисковую ставку. Сосчитал по Б-Ш цены для разных страйков и времени до экспирации. Отнормировал цены на единицу в начальный момент времени. Ну и нарисовал график :)

tte.seq <- seq(from = 1, to = 1 / 365, by = -1 / 365)

px.calls <- do.call(
  cbind,
  lapply(
    seq(from = 0, to = 25, by = 5),
    function (otmness) {
      ret.val <- sapply(
        tte.seq,
        function (tte) {
          fOptions::GBSOption(
            TypeFlag = 'c',
            S = 100, # underlying px
            X = 100 + otmness, # strike
            Time = tte,
            r = 0.02, b = 0.02, # risk-free rate
            sigma = 0.125 # implied vol
            )@price
        }
        )
      (ret.val / ret.val[1])
    }
    )
  )

matplot(tte.seq, px.calls, t = 'l', lty = 'solid', xlab = 'T', ylab = 'value left')
abline(h = seq(from = 0, to = 1, by = 0.1), lty = 'dashed', col = 'grey')
legend(
  'topleft',
  pch = 20,
  col = seq_along(seq(from = 0, to = 25, by = 5)),
  legend = sprintf('%.2f%% OTM', seq(from = 0, to = 25, by = 5))
  )

Кирилл Браулов, https://www.voladynamics.com/src/pdf/volcurves_CU_24Mar2016.pdf
(у меня эта ссылка открывается только через Tor)

Картинка про AMZN от них же: https://www.voladynamics.com/marketEquityUS_AMZN.html

ch5oh, 

интересно: у меня не показывается список тех, кто «избрал» коммент...

Чужое избранное можно посмотреть :)

"Но применить её как-то не смог. "

Из того, что кто-то не смог что-то применить, не следует, что применить не получится у другого. А взять на вооружение методы, вскользь упомянутые конкурентами (или просто умными и опытными людьми) — это просто моя обязанность!

ch5oh, Malik Magdon-ismail, Amir Atiya, Amrit Pratap, Yaser S. Abu-mostafa «On the maximum drawdown of Brownian motion»;) Но даже если просто монте-карлить величину просадки в зависимости от горизонта (ъуъ, сколько раз я это делал!) — сложно не заметить этого свойства, если у вас есть привычка смотреть на данные не только в линейном, но и в логарифмическом масштабе по разным осям.

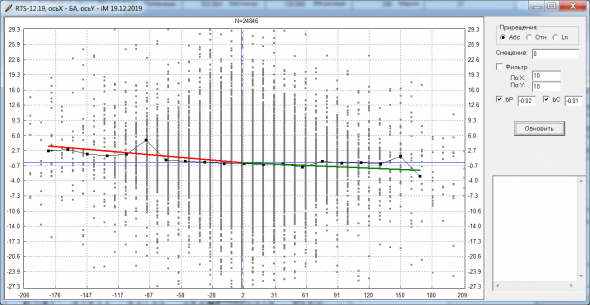
Так понял, что как только речь заходит о вероятностном описании экстремумов случайного процесса внезапно всё становится очень сложно.

Для практических целей ответы на многие вопросы можно получить численно.
Кстати, вы уже раздобыли себе книгу, которую когда-то упомянул SergeyJu?

Вчера в самолёте начал читать. Довольно урчу от первых впечатлений ;)

Андрей Хрущев, У дальних опционов волатильность растет меньше в %, но больше в реальном выражении. К тому же их количество больше. Этот момент проверен практикой. В данной позиции у меня была проблема с падением волатильности.
Соотношение 14:10:2 выбирал как самое подходящее для такой ситуации. Чисто визуально на профиле позиции смотреть надо. Вообще то, это соотношение 7:5:1. Но для сравнение его с фьючерсом (в прошлом посте) пришлось его удвоить.
Соотношения могут быть любые по формуле: (N опционов покупаем):(N-2 опционов продаем): (1 фьючерс покупаем/продаем в зависимости путы это или коллы)

ch5oh, уже смотрю удалили в инете они. 
Кинул в облако, завтра удалю ссылка 

ch5oh, рад слышать, давно не общались

Тема пока сыровата для публикации и не так красива, как это бывает в книжках. Поэтому напишу нескоро, наверное. Но могу сразу отметить 2 обескураживающих результата:
1. Может оказаться, что max(return/dd) стремится к бесконечности при увеличении длины интервала. Это я про FX, если что. Понятно, что в дискретном случае все это кажется бессмысленным, но настораживает уверенный рост на логарифмической шкале времени. Надо бы обработать более 5 млн. отсчетов (сейчас до 300 тыс.), можно больше, тогда можно будет уверовать окончательно. До этого руки пока не доходят.
2. Оптимальная стратегия может зависеть не только от ценового ряда, но и от способа исполнения приказов (лимитные и маркет-ордера). Разумеется, в теоретических рассуждениях мы предполагаем отсутствие комиссий и проскальзывания. Такой феномен наблюдается на рынках, где ликвидность не обеспечивается маркетмейкером, а покупается за счет рибейтов (большая часть крипты, акции NYSE и NASDAQ, ...).

На последнюю тему я планирую опубликовать небольшую статью под рабочим названием «Неевклидова геометрия лимитных ордеров». Здесь материал уже собран — осталось оформление. К сожалению, до НГ я плотно занят своим проектом, на праздники что-нибудь наваяю.

Там есть свои чудеса:
1. Если система, работающая лимитниками, убыточна, то обратная к ней система (инвертируем сигнал), также может быть убыточна.
2. Если система, работающая лимитниками, прибыльна, ее можно однозначно преобразовать в систему, прибыльно работающую при маркет-исполнении
3. Обратное неверно, для этого система должна быть инвариантна для некоего набора линейных преобразований цены.

С уважением

P.S. Всегда завидовал людям, которые считают, что рынок устроен просто

А. Г., с практической точки зрения даже изображение в современных задачах по распознанию это пространство хоть и конечное, но имеющее размер порядка 256^3^(500 * 500), что можно считать вполне бесконечным с практической точки зрения. В звуке еще больше.
Базовые архитектуры сетей для вероятностного анализа временных рядов можно посмотреть в этой библиотечке https://gluon-ts.mxnet.io/index.html
Про конкретное применение ML для предсказания будущих котировок по динамике стакана слушал только в эти выходные (видио):
Победителем было построено 50 моделей с помощью градиентного бустинга (на базе LightGBM)
Предсказание этих моделей было объединено с помощью ElasticNet (на базе sklearn)

ch5oh,

Но тогда надо учиться фитить его параметры. Особенно уровень притяжения.

Логарифм волатильности можно приближенно считать процессом OU.

Про калибровку — вот тут ссылку кидал. Параметры OU выражаются из коэффициентов регрессии. Чтобы учесть изменения параметров — можно оценивать коэффициенты регрессии фильтром Калмана или вот такими штуками.

А ценители прекрасного могут попытаться скрестить оценивание при помощи MLE с SPRT. Или сразу соорудить PF :)