bstone, Да, конечно мы живем в рамках «одного шага управления портфелем». Можно сказать «в его самом начале».

Итак, будем считать мы договорились, что в этот начальный момент времени

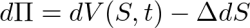
тогда раскладываем dV в ряд Тейлора по его аргументам и выбрасываем члены второго и выше порядка:

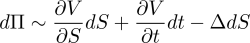
Собственно, уже в этот момент времени по определению

(тета) и
(дельта)

Теперь ставится задача: получить иммунитет к движению БА (то есть утранить зависимость от dS). Согласны? Это все еще классическая теория. Мы еще даже про модель динамики цены ничего не сказали.

При этом возникает тонкий момент. С одной стороны у нас вроде как имеется зависимость от времени (пресловутая тета), с другой стороны в классической литературе не хотят обсуждать очень интересную задачку "Устранение зависимости цены портфеля от движения цены БА на конечном горизонте времени (час, день, неделя, 5 минут, и т.д.)" (или мне не попадалась исчерпывающее решение к моему большому сожалению).

Тогда мы говорим: "делаем ДХ непрерывно. dt -> 0".При большом времени до экспирации и очень маленьком интервале ДХ тетой пренебрегаем. Формальное обоснование этого требует конкретизации модели процесса и написание какого-нибудь подходящего уравнения. Привет Блеку-Шолзу. В конечном итоге цель этих действий состоит в том, чтобы показать, что {\Theta} dt имеет второй порядок малости по сравнению с dS

После чего не остается никаких вариантов, кроме как признать, что для иммунизации портфеля от малых колебаний цены на малых временах времени величина "количество фьючерсов" {\Delta} обязана быть равной частной производной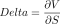

Если мы все это освежили и проговорили, то теперь есть большой простор для маневра.

Можно ставить задачу минимизации другой функции. Можно использовать другую модель процесса. Тогда, вероятно, «коэффициент хеджа» тоже станет другой. Можно учитывать тету и интервал хеджирования. И т.д. и т.п.

Ваш ход.

ПС Поскольку это выражение будет нужно ниже в ответе bstone приведу его здесь.

Итак, после всех рассуждений слагаемое с тетой отбрасывается и остается упрощенное выражение для дифференциала стоимости портфеля (справедливое только для каких-то конкретных типов случайных процессов):