Избранное трейдера Villcommen
Новичкам. Как подсчитать HV для фьюча Ri? Для чего нужна Дисперсия?
- 17 мая 2020, 12:13
- |
С вами снова опционный уголок и сегодня мы на половину спалим Грааль опционщиков, чтобы им больше жизнь малиной не казалась.
Классические опционщики бьют себя всё время в грудь, утверждая, что голые конструкции они не торгуют, голые конструкции торгуют видите ли лишь опционные лохи, а они, мол, такие крутые, торгуют волатильность. Что это значит?
Всё очень просто. Они высчитывают всего лишь 2 параметра: IV и HV, где
IV — ожидаемая волатильность,
HV — историческая волатильность.
Если IV>HV, то они продают волатильность, если IV<HV, то они покупают волатильность.
Как всё просто, да?
Просто. Но есть очень много нюансов.
Сегодня разберемся с одним из параметров, а именно с HV.
Историческая волатильность.
Историческая волатильность определяется как стандартное отклонение логарифмических изменений цены, взятых через равные интервалы времени. Поскольку наиболее надежными обычно считаются расчетные цены, самый распространенный метод определения волатильности предполагает использование именно изменений расчетной цены (а есть еще способ, когда мы не знаем расчетных цен, а знаем максимумы и минимумы, считаем через них, но нам это неинтересно).
( Читать дальше )
- комментировать
- 5.9К | ★29
- Комментарии ( 67 )
Статья про налоги. Прочтите пожалуйста.
- 06 мая 2020, 19:12
- |
Статья про налоги. Прочтите пожалуйста. 3-НДФЛ

Доброго времени суток, коллеги!
Сегодня в своей статье я опишу крайне важную и объемную тему, с которой рекомендую ознакомиться всем.
Покажу на примере Interactive Brokers.
У других брокеров аналогичная схема.
Итак, начнем
В статье будет идти повествование по налогообложению резидентов. Данная информация поможет Вам ориентироваться на рынке ценных бумаг. Информация будет полезной, как инвесторам, так и спекулянтам.
Кто признается налоговым резидентом: признаются граждане РФ, иностранные граждане, лица без гражданства, если они находится на территории РФ более 183 календарных дней в течение 12 следующих подряд месяцев. Период нахождения физического лица в Российской Федерации не прерывается на периоды выезда физического лица за пределы Российской Федерации для краткосрочного (менее шести месяцев) лечения или обучения, а также для исполнения трудовых или иных обязанностей, связанных с выполнением работ (оказанием услуг) на морских месторождениях углеводородного сырья. И другие.
( Читать дальше )
- комментировать
- 12.3К |
- Комментарии ( 45 )
Кто не понял, тот поймёт или меняю бочку нефти на бусы из ракушек и зеркальце.
- 05 мая 2020, 09:03
- |
1995: 4,9
2000: 9,5
2006: 12,7
2008: 16,5
2010: 20,5
2012: 22,2
2014: 23,8
2016: 22,7
2018: 25,5 Росстат
--------------------
Италия — Manufacturing PMI (апр) = 31.1 (пред 40.3)
Франция — Manufacturing PMI (апр) = 31,5 (пред 43.2)
Германия — Manufacturing PMI (апр) = 34,5 (пред 45.4)
Еврозона — Manufacturing PMI (апр) = 33.4 (пред 44.5)
--------------------
РФ. Число семей (включая одиноких), получивших жилые помещения и улучшивших жилищные условия, тыс
1990: 1296
1995: 652
2000: 253
2004: 229
2008: 144
2010: 244
2012: 186
2014: 138
2018: 99 Росстат
--------------------
Процент по ипотеке на жилье в США упал до минимального значения с 1971. Если на 30 лет, то по 3.23%, на 15 лет по 2.77%
--------------------
Претендовать на безвозмездные гранты в РФ со стороны государства не смогут две трети малого и среднего бизнеса — «за бортом» останутся 4,24 млн компаний и ИП, не относящихся к пострадавшим от коронавируса отраслям. FinExpertiza
( Читать дальше )
Анализ акций языком, понятным даже вашей бабушке
- 19 апреля 2020, 16:06
- |
Я страшно злюсь на инвесторов. Еще злюсь на бухгалтеров. Из книжки в книжку, из статьи в статью гуляют определения, при виде которых простой смертный начинает хлопать глазами. Его мозг перестает воспринимать информацию.
Неужели так сложно объяснить простыми словами то, что лежит на поверхности? Давайте попробуем разобраться.
Представьте, если вы вдруг захотите купить какой-нибудь маленький бизнес. Салон красоты, палатку с шаурмой, ресторан. Что угодно. Какие вопросы вы будете задавать продавцу:
- Вы вообще прибыльны?
- Через сколько мои вложения окупятся?
- На что тратите больше всего?
- Есть ли у вас долги?
( Читать дальше )
- комментировать
- 15.6К |
- Комментарии ( 0 )
Зигзаг удачи - 1 апреля 2020
- 02 апреля 2020, 00:32
- |
Кризис приятен тем, что даёт возможность потренировать разные позиции. Никому не интересно читать однотипные под копирку посты «продал стреддл — зафиксировал прибыль». Даже одиночный возглас "будь прокляты хуситы и охрана завода саудитов!" общей картины не менял. Хоть новоявленный опционный псевдогуреныш Г… ая Г… нь и считает, что «торговать мосбиржу западло» и «торговать в кризис дважды западло», но кто он такой, чтобы нам указывать? Поэтому караван идет и на пути ему попался Зигзаг Удачи.
Эта позиция считается базовой уважаемым Каленкович Алексей (enki) .
Низкий ему поклон за науку и за время, которые он мне уделил.
Давным-давно в уже далеком 2017 году эта позиция так и торговалась из месяца в месяц методично и довольно скучно (до февраля 2018 года примерно =) ) на боевом тестовом счете (размером около 100 тыр). Учитывая, что это были месячные опционы на РИ сейчас сам себе удивляюсь, насколько хватало смелости переносить это всё хозяйство через ночь и выходные. =) Nobless oblige
( Читать дальше )
Про греки и сбор теты. Опять по новой :)
- 31 марта 2020, 11:35
- |
Про греки.
Сразу предупреждаю. Следующие три ссылки — ссылки на мой сайт (никаких регистраций не нужно).
Все, что я хотел сказать в открытом доступе, я сказал здесь. Даже сделал чек-лист по грекам (здесь). И еще написал алгоритм действий при создании опционной позиции (здесь).
По-моему, уже здесь выкладывал, но выложу еще раз:
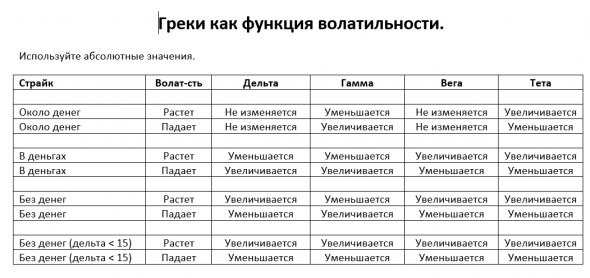
Идея создания опционов – это попытка оценить будущий диапазон движения БА. Отсюда и идет то, что профессионалы при торговле опционами смотрят на историческую волатильность (HV), подразумеваемую волатильность (IV) и пытаются спрогнозировать будущую реализованную волатильность. Затем, участники рынка пытаются спрогнозировать, какой будет волатильность БА, если его цена вырастет/упадет на 1,2,3 и т.д. процента. Так появляется кривая волатильности. Затем начинают прогнозировать движение БА за различный временной интервал, что приводит нас к временной структуре.
( Читать дальше )
1 апреля - прекратится действие соглашение ОПЕК+ и начнется самое интересное - торговля реальной нефтью, а не фьючерсами
- 31 марта 2020, 00:26
- |
https://lt.sputniknews.ru/columnists/20200330/11744045/Na-Zapad-i-Vostok-rasschitaysya-Est-li-u-RF-i-Kitaya-superplan-naschet-nefti.html
Спрос на нефть в Китае продолжает опережать его собственную добычу, объем китайского рынка, динамика роста промышленности делают эту страну самым перспективным рынком для любой нефтедобывающей компании, для любого государства, в экономике которого имеется отрасль добычи углеводородов.
Именно по этой причине нефтяной рынок Китая уже несколько лет является «эпицентром» конкуренции нефтяников всего мира, в том числе нефтяных компаний России, США и Saudi Aramco, государственного углеводородного монополиста Королевства Саудовская Аравия (КСА). На мой взгляд, это аксиома, которая позволяет объяснить все, что происходило с соглашением ОПЕК+ в декабре 2019-го и в марте 2020 года.
Пара слов о сортах нефти

( Читать дальше )
- комментировать
- 19.5К |
- Комментарии ( 37 )
Один раз - и только для вас: Опционные беседы со Старым Бесом. Бесплатно, без SMS
- 27 марта 2020, 14:25
- |
© Торгуйте опционами, и да пребудет с нами нелинейность, ликвидность и волатильность по целям
Опционные беседы
Вега и Вомма
- 15 марта 2020, 03:27
- |
Возможно, не все знают про нелинейные эффекты грека Веги и волшебные свойства грека Воммы. По нынешним волатильным временам, когда вола ходит туда-сюда на десятки процентов — эти эффекты могут значительно повлиять на финрез при торговле волатильностью. Хочу поделиться своим видением — может кому будет интересно. А может кого убережет от опасной позиции с неоправданным риском.
Итак, рассмотрим проданный стрэдл:
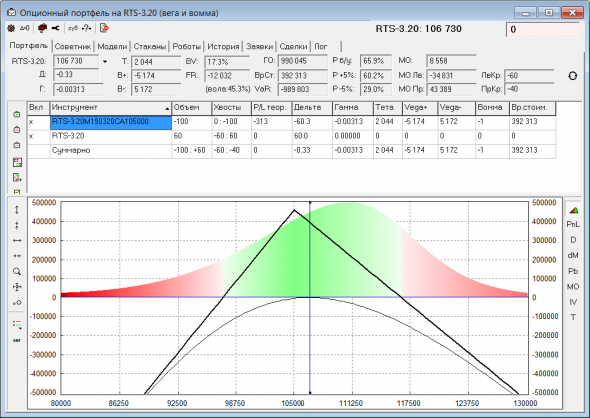
Это обычный профиль PnL, который рисуют все опционные программы. Фактически, это зависимость PnL позиции от первого момента (M1) распределения вероятностей, где окажется цена БА на экспирацию (вон оно на заднем фоне профиля). M1 = текущей цене БА. Т.е. мысленно двигаем все распределение влево-вправо (меняем M1) и считаем, как изменится PnL позиции при этом. Но, когда торгуем волатильностью, влияние первого момента ведь стараемся исключать используя дельтахедж (ДХ). И в большей степени нас должен интересовать профиль PnL от второго момента распределения (M2). Именно от него зависит финрез торговли волатильностью. Фактически, M2 почти тоже самое, что IV на центре улыбки (IVC). Смотрел на истории, специальным образом нормированный M2 (на цену БА и время до экспы) коррелирует с IVC почти 100%.
Если у нас есть опционная модель, в которой можно точечно менять второй момент, то легко посмотреть профиль PnL от изменений M2. Я использую замечательную модель Курбаковского, в которой главный параметр mI — как раз и отвечает за второй момент. Поэтому добавил в своей программе отрисовку такого профиля. И вот что рисует для проданного стрэдла:
( Читать дальше )
Новичкам. Дельта-хеджирование. Как прогнозировать куда пойдет цена при помощи дельты?
- 14 марта 2020, 20:05
- |
Продолжаем грызть тему опционов по рекомендуемой ранее литературе (см.здесь).
Сегодня мы добрались до темы «Дельта и хеджирование стратегий".
Изучив данный материал, мы окажемся на 115 странице книги, а это значит, что в теме опционов на текущий момент ваш покорный слуга прокачан всего лишь на 115/400=29%.
Понравилось то, как пишет Саймон по теме греков:
Чтобы узнать больше об опционах, необходимо изучить так называемые «греки» (параметры риска опционов, названные буквами греческого алфавита). Не пугайтесь абстрактного характера этих терминов. Большинство трейдеров не имеют математического образования! Советуем вам наглядно представить практическое значение этих показателей или просто зазубрить их. В дальнейшем это обязательно сработает.
Самый важный параметр опционов — дельта. Это отношение изменения премии опциона к изменению цены базового актива. Дельта показывает, насколько изменится премия опциона, если цена базового актива изменится на один пункт. Например, цена длинного опциона колл с дельтой 20 увеличится на 0,2 пункта при росте цены базового актива на 1 пункт.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал

