SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Избранное трейдера MrD
Возвращаю должок: инвесторы-новички, вы НЕ можете потерять на бирже все!
- 27 февраля 2022, 11:11
- |

Один год и 11 дней назад я опубликовал пост, который оспаривал другой пост смартлабовского Главного о том, что все пропало, и инвесторы-новички могут потерять на бирже все. Очень кратко, мои аргументы были следующими:
— рынки ни в России, ни даже в США не переоценены
— инвесторы (по крайней мере в России) НЕ покупают акции в огромных объемах, в частности, за год, предшествующий времени написания того поста, на рынок было заведено всего 15% от суммы выплаченных за тот год дивидендов
— если вы тру-инвестор, то торгуете без плеч и радуетесь падениям, а если не совсем тру — можете использовать инструменты ограничения убытков, такие как «продавать ниже 200-дневного скользящего среднего» и диверсификация.
В ответ я получил от «управляющего деньгами одного миллиардера», на криках «фсепропало» которого и был основан мартыновский пост, следующее сочинение:
( Читать дальше )
- комментировать
- ★5
- Комментарии ( 29 )
И в очередной раз про применимость методов ТВиМС к рыночным ценам
- 15 февраля 2022, 04:10
- |
Доброй ночи, коллеги!
Хочу задать простой вопрос (в уточнение предыдущих дискуссий)
Я правильно понимаю, что для применения методов теории вероятностей и математической статистики к анализу рыночных цен изначально надо быть уверенным в том, что:
1. Приращения цен стараются не сильно отклоняться от своего среднего значения
2. Квадраты отклонений приращений цен от их среднего значения также должны вести себя достойно
В противном случае любая вероятностная модель может столкнуться с распределением приращений цен типа распределения Коши. Которая не только странна сама по себе, но и делает плохоприменимыми стандартные экономометрические плюшки (МНК etc.).
ВОПРОС:
Почему, коллеги, Вы считаете, что методы ТВиМС успешно применимы к рынку?
К примеру, в вопросе предсказания погоды методы ТВиМС факапят с 1960 г., наверное… Хотя погода тоже случайна… Не?
С уважением и в ожидании конструктивных ответов
И как обычно — убедительная просьба не срать в блоге. Для политики я создал отдельный блог.
С уважением
Хочу задать простой вопрос (в уточнение предыдущих дискуссий)
Я правильно понимаю, что для применения методов теории вероятностей и математической статистики к анализу рыночных цен изначально надо быть уверенным в том, что:
1. Приращения цен стараются не сильно отклоняться от своего среднего значения
2. Квадраты отклонений приращений цен от их среднего значения также должны вести себя достойно
В противном случае любая вероятностная модель может столкнуться с распределением приращений цен типа распределения Коши. Которая не только странна сама по себе, но и делает плохоприменимыми стандартные экономометрические плюшки (МНК etc.).
ВОПРОС:
Почему, коллеги, Вы считаете, что методы ТВиМС успешно применимы к рынку?
К примеру, в вопросе предсказания погоды методы ТВиМС факапят с 1960 г., наверное… Хотя погода тоже случайна… Не?
С уважением и в ожидании конструктивных ответов
И как обычно — убедительная просьба не срать в блоге. Для политики я создал отдельный блог.
С уважением
Как конкретно зарабатывать на рынке?
- 10 февраля 2022, 00:59
- |
Доброй ночи, коллеги!
На рынке можно зарабатывать разными способами.
Лично я использую портфель реверсивных систем, основанных на линейных индикаторах.
Линейные индикаторы — это нечто, известное всем. МАшки — это линейный индикатор. Боллинджер — это уже нелинейный индикатор.
Давным давно я выяснил (и несколько лет назад опубликовал на СЛ), что нашел оптимальный стационарный линейный индикатор — и он показывает более, чем слабые результаты на долгосроке. Ну т.е. всегда работает в плюс, но плюс на сделку (обычно) не превышает спрэд, поэтому разбогатеть на этом невозможно.
3 года назад я открыл для себя эффективно работающие нестационарные линейные индикаторы — и сделал первый шаг на пути к Граалю.
ВОПРОС:
1. Вы используете стационарные индикаторы? (не меняете их параметры долгое время)
2. Или перестраиваете коэффициенты индикатора на каждом баре? (это правильно)
С уважением
На рынке можно зарабатывать разными способами.
Лично я использую портфель реверсивных систем, основанных на линейных индикаторах.
Линейные индикаторы — это нечто, известное всем. МАшки — это линейный индикатор. Боллинджер — это уже нелинейный индикатор.
Давным давно я выяснил (и несколько лет назад опубликовал на СЛ), что нашел оптимальный стационарный линейный индикатор — и он показывает более, чем слабые результаты на долгосроке. Ну т.е. всегда работает в плюс, но плюс на сделку (обычно) не превышает спрэд, поэтому разбогатеть на этом невозможно.
3 года назад я открыл для себя эффективно работающие нестационарные линейные индикаторы — и сделал первый шаг на пути к Граалю.
ВОПРОС:
1. Вы используете стационарные индикаторы? (не меняете их параметры долгое время)
2. Или перестраиваете коэффициенты индикатора на каждом баре? (это правильно)
С уважением
Про фильтры от скуки.
- 05 февраля 2022, 00:38
- |
За ужином принял полстакана ее — родимой. Ну, по объему, принимал рюмками, даже полрюмками, чтобы посмаковать.
Скучно, кризис желаний, не хочется ничего, даже денег. Впрочем, денег уже давно не хочется — зачем, их и так хватает. Ну, может не на все, но это не обязательно и даже лишнее. А куда их? Солить? Про деньги и инвестиции я всегда вспоминаю:
Впрочем, хотелось о фильтрах, которые я применяю для своих систем. Уникальный случай — все фильтры в сборе. Смотрите.
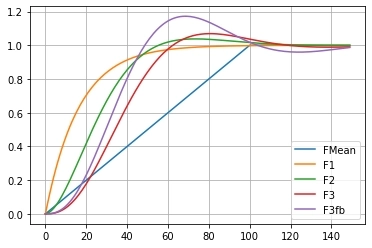
FMean — это по вашему SMA, а по мне просто среднее за период - предназначен в основном для калибровки. F1 — это та же ЕМА, только с другим нормированием, и потому уже и не ЕМА.)
( Читать дальше )
Скучно, кризис желаний, не хочется ничего, даже денег. Впрочем, денег уже давно не хочется — зачем, их и так хватает. Ну, может не на все, но это не обязательно и даже лишнее. А куда их? Солить? Про деньги и инвестиции я всегда вспоминаю:
Как молодой повеса ждет свиданья С какой-нибудь развратницей лукавой Иль дурой, им обманутой, так я Весь день минуты ждал, когда сойду В подвал мой тайный, к верным сундукам. Счастливый день! могу сегодня я В шестой сундук (в сундук еще неполный) Горсть золота накопленного всыпать. Не много, кажется, но понемногу Сокровища растут.На это вы себя расходуете?
Впрочем, хотелось о фильтрах, которые я применяю для своих систем. Уникальный случай — все фильтры в сборе. Смотрите.

FMean — это по вашему SMA, а по мне просто среднее за период - предназначен в основном для калибровки. F1 — это та же ЕМА, только с другим нормированием, и потому уже и не ЕМА.)
( Читать дальше )
QLua: таблица крупных "склеенных" обезличенных сделок - 2
- 25 января 2022, 09:43
- |
Недавно ко мне обратился один из смартлабовцев с просьбой доработать скрипт из поста https://smart-lab.ru/blog/610116.php, чтобы можно было более гибко подходить к раскраске выводимой там таблицы крупных «склеенных» сделок. Я решил проделать эту работу и выложить сюда модернизированный скрипт.
Настройки раскраски таблицы производятся в самом скрипте. Я сделал какие-то настройки для светлой темы терминала, может быть, весьма далёкие от ваших идеалов. Каждый пользователь пусть настраивает сам на свой вкус через палитру RGB (для каждого из трёх основных цветов нужно выбрать интенсивности от 0 до 255), редактируя строки в начале основного скрипта.
Для работы скрипта нужен собственно сам скрипт и один или несколько файлов настроек для ваших наборов инструментов. Границы крупных и очень крупных сделок, проскальзывания и «многосоставности» сделок также пользователи настраивают под себя. В терминале QUIK запускается файл с настройками, а он в свою очередь запускает основной скрипт.
( Читать дальше )
Настройки раскраски таблицы производятся в самом скрипте. Я сделал какие-то настройки для светлой темы терминала, может быть, весьма далёкие от ваших идеалов. Каждый пользователь пусть настраивает сам на свой вкус через палитру RGB (для каждого из трёх основных цветов нужно выбрать интенсивности от 0 до 255), редактируя строки в начале основного скрипта.
Для работы скрипта нужен собственно сам скрипт и один или несколько файлов настроек для ваших наборов инструментов. Границы крупных и очень крупных сделок, проскальзывания и «многосоставности» сделок также пользователи настраивают под себя. В терминале QUIK запускается файл с настройками, а он в свою очередь запускает основной скрипт.
( Читать дальше )
Как торговая система гарантирует положительное матожидание?
- 25 января 2022, 01:19
- |
Доброй ночи, коллеги!
Тут один уважаемый чел в соседнем топике написал, что «торговая система должна гарантировать положительное матожидание».
Конечно, это было бы здорово. Но как система может что-то гарантировать?
Призадумался я — и вспомнил старый анекдот:
Стоит мужик у букмекерского окна на ипподроме и думает, на какую бы лошадь поставить. Тут подходит к нему старая кобыла и говорит: «Ставь на меня, мужик. Я хоть и старенькая, но раньше чемпионкой была, и сегодня в отличной форме! На меня больше никто не ставит, выиграю забег – сорвешь большой куш!».
Подумал-подумал мужик и поставил на кобылу все деньги. Начинается заезд, кобыла дергается с места, делает несколько шагов, падает на землю и больше не поднимается. Мужик подходит к ней после забега с угрожающим видом. Кобыла смотрит на него виновато и шепелявит: «Ну не шмогла я, не шмогла».
Что вы думаете по этому поводу, коллеги?
С уважением
Тут один уважаемый чел в соседнем топике написал, что «торговая система должна гарантировать положительное матожидание».
Конечно, это было бы здорово. Но как система может что-то гарантировать?
Призадумался я — и вспомнил старый анекдот:
Стоит мужик у букмекерского окна на ипподроме и думает, на какую бы лошадь поставить. Тут подходит к нему старая кобыла и говорит: «Ставь на меня, мужик. Я хоть и старенькая, но раньше чемпионкой была, и сегодня в отличной форме! На меня больше никто не ставит, выиграю забег – сорвешь большой куш!».
Подумал-подумал мужик и поставил на кобылу все деньги. Начинается заезд, кобыла дергается с места, делает несколько шагов, падает на землю и больше не поднимается. Мужик подходит к ней после забега с угрожающим видом. Кобыла смотрит на него виновато и шепелявит: «Ну не шмогла я, не шмогла».
Что вы думаете по этому поводу, коллеги?
С уважением
Рыночные цены и "стрела времени"
- 24 января 2022, 00:03
- |
Доброй ночи, коллеги!
Хочу задать интересный вопрос, ну, или устроить интересную (для меня точно) дискуссию)
За 2 последних дня я провел ряд численных экспериментов, которые могут показывать, что ряды рыночных цен (возможно) обратимы во времени.
Нет, машину времени я не изобрел. Но определенные типы индикаторов одинаково хорошо работают (не теряют свою предсказательную способность в хорошем смысле этого слова, т.е. несут бабло, пока без учета издержек) и при обычном времени, и при инвертированном (текущем вспять).
Вроде бы в этом нет ничего необычного:
1. Если рынки подчиняются законам EWT (волновая теория Эллиотта), то все паттерны вроде симметричны к обращению времени
2. Если на рынке рулят МАшки etc. — тоже не наблюдается никаких нарушений симметрии времени
Однако:
1. Если рынок — это случайное блуждание (или геометрическое СБ) — то энтропия возрастает, не?
2. Если рыночные цены суть сумма независимых приращений цены с меняющимися МО и Д, то что?
3. Если рыночные цены суть сумма зависимых приращений цены с отрицательной корреляцией, то что?
( Читать дальше )
Хочу задать интересный вопрос, ну, или устроить интересную (для меня точно) дискуссию)
За 2 последних дня я провел ряд численных экспериментов, которые могут показывать, что ряды рыночных цен (возможно) обратимы во времени.
Нет, машину времени я не изобрел. Но определенные типы индикаторов одинаково хорошо работают (не теряют свою предсказательную способность в хорошем смысле этого слова, т.е. несут бабло, пока без учета издержек) и при обычном времени, и при инвертированном (текущем вспять).
Вроде бы в этом нет ничего необычного:
1. Если рынки подчиняются законам EWT (волновая теория Эллиотта), то все паттерны вроде симметричны к обращению времени
2. Если на рынке рулят МАшки etc. — тоже не наблюдается никаких нарушений симметрии времени
Однако:
1. Если рынок — это случайное блуждание (или геометрическое СБ) — то энтропия возрастает, не?
2. Если рыночные цены суть сумма независимых приращений цены с меняющимися МО и Д, то что?
3. Если рыночные цены суть сумма зависимых приращений цены с отрицательной корреляцией, то что?
( Читать дальше )
О тернистом пути применения методов ТВиМС в трейдинге
- 22 января 2022, 04:23
- |
Доброй ночи, коллеги!
Сам я не поклонник применения методов ТВиМС в трейдинге (только когда по-другому никак), но свое частное мнение никому не навязываю.
Однако на этом пути пытливого исследователя могут ждать серьезные вычислительные проблемы, которые надо уметь решать.
1. Для максимизации эквити (или ее приращения на баре) очень важно наблюдать за произведениями приращений цен (условно d(i)*d(i-1)). Не хочу никого убеждать, прошу просто поверить на слово.
2. Известно (я приводил массу примеров), что соседние приращения цен не только не являются независимыми, но весьма сильно коррелированы.
3. Допустим, что приращения цен распределены нормально (сам я в это не верю, но признаю, что это общепринятая точка зрения).
ВОПРОС:
Как устроена плотность вероятности распределения случайной величины d(i)*d(i-1), если d(i) и d(i-1) — это зависимые нормально распределенные случайные величины с коэффициентом корреляции r? (разумеется, матожидания и дисперсии также известны)
С уважением
P.S. Эта задача не требует хорошего знания математики — достаточно знать профильные термины и уметь пользоваться поиском Google (хотя решения, полученные руками, всячески приветствуются). Однако, итоговая формула доставляет )))
Сам я не поклонник применения методов ТВиМС в трейдинге (только когда по-другому никак), но свое частное мнение никому не навязываю.
Однако на этом пути пытливого исследователя могут ждать серьезные вычислительные проблемы, которые надо уметь решать.
1. Для максимизации эквити (или ее приращения на баре) очень важно наблюдать за произведениями приращений цен (условно d(i)*d(i-1)). Не хочу никого убеждать, прошу просто поверить на слово.
2. Известно (я приводил массу примеров), что соседние приращения цен не только не являются независимыми, но весьма сильно коррелированы.
3. Допустим, что приращения цен распределены нормально (сам я в это не верю, но признаю, что это общепринятая точка зрения).
ВОПРОС:
Как устроена плотность вероятности распределения случайной величины d(i)*d(i-1), если d(i) и d(i-1) — это зависимые нормально распределенные случайные величины с коэффициентом корреляции r? (разумеется, матожидания и дисперсии также известны)
С уважением
P.S. Эта задача не требует хорошего знания математики — достаточно знать профильные термины и уметь пользоваться поиском Google (хотя решения, полученные руками, всячески приветствуются). Однако, итоговая формула доставляет )))
Для любителей статистического анализа (квартет Энскомба)
- 21 января 2022, 23:24
- |
Статистика - это такой инструмент… Очень страшный в неумелых руках.
В умелых руках и того страшнее — способен разорвать мозг на куски.
Вот есть наборы данных (с двумя переменными x и y) I, II, III и IV, про которые известны следующие их свойства:
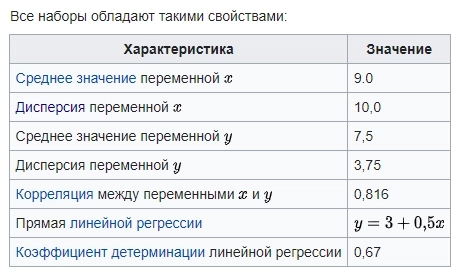
Квартет Энскомба — четыре набора числовых данных, у которых простые статистические свойства идентичны, но их графики существенно отличаются. Каждый набор состоит из 11 пар чисел. Квартет был составлен в 1973 году английским математиком Ф. Дж. Энскомбом.
Сами последовательности приведены ниже. Значение x одинаковы для первых трёх последовательностей.
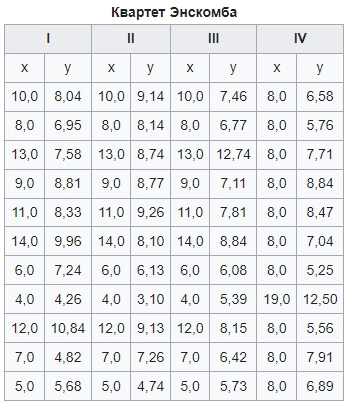
( Читать дальше )
В умелых руках и того страшнее — способен разорвать мозг на куски.
Вот есть наборы данных (с двумя переменными x и y) I, II, III и IV, про которые известны следующие их свойства:

Квартет Энскомба — четыре набора числовых данных, у которых простые статистические свойства идентичны, но их графики существенно отличаются. Каждый набор состоит из 11 пар чисел. Квартет был составлен в 1973 году английским математиком Ф. Дж. Энскомбом.
Сами последовательности приведены ниже. Значение x одинаковы для первых трёх последовательностей.

( Читать дальше )
Интересная трейдерская задача по теории вероятностей
- 20 января 2022, 00:05
- |
Доброй ночи, коллеги!
С удовольствием презентую уважаемому community интересную задачу из области теории вероятностей.
Решение задачи (когда оно получено) имеет непосредственное отношение к трейдингу.
Итак:
Имеем 3 (возможно, зависимые) случайные величины X1, X2 и X3.
Про них известны МО (матожидания) M1, M2 и M3, Д (дисперсии) D1, D2 и D3 и ковариации C12, C13 и C23.
Теперь составляем линейную комбинацию A1*X1+A2*X2+A3*X3 с неизвестными (пока) коэффициентами A1, A2 и A3.
Требуется найти коэффициенты A1, A2 и A3, при которых соотношение МО/sqrt(Д) для линейной комбинации будет максимальным.
(sqrt — это по-русски просто квадратный корень)
Жду ваших ответов и мнений, коллеги.
С уважением
P.S. 3 величины (а не N) выбраны для упрощения. Для 2-х случайных величин задача тривиальна.
P.P.S. Задача не слишком проста, и, по хорошему, следовало бы объявить платный конкурс. Но:
1. Я не знаю лично ни одного человека, которого забанили бы в Google (хотя поиск в Google не так прост на самом деле...)
2. (почти) Всем доступны пакеты символьной математики (Mathematica, Matllab, Maple), которые позволяют решать сложные задачи, не задумываясь об их устройстве и не владея математикой (но хорошо владея профильным софтом).
С удовольствием презентую уважаемому community интересную задачу из области теории вероятностей.
Решение задачи (когда оно получено) имеет непосредственное отношение к трейдингу.
Итак:
Имеем 3 (возможно, зависимые) случайные величины X1, X2 и X3.
Про них известны МО (матожидания) M1, M2 и M3, Д (дисперсии) D1, D2 и D3 и ковариации C12, C13 и C23.
Теперь составляем линейную комбинацию A1*X1+A2*X2+A3*X3 с неизвестными (пока) коэффициентами A1, A2 и A3.
Требуется найти коэффициенты A1, A2 и A3, при которых соотношение МО/sqrt(Д) для линейной комбинации будет максимальным.
(sqrt — это по-русски просто квадратный корень)
Жду ваших ответов и мнений, коллеги.
С уважением
P.S. 3 величины (а не N) выбраны для упрощения. Для 2-х случайных величин задача тривиальна.
P.P.S. Задача не слишком проста, и, по хорошему, следовало бы объявить платный конкурс. Но:
1. Я не знаю лично ни одного человека, которого забанили бы в Google (хотя поиск в Google не так прост на самом деле...)
2. (почти) Всем доступны пакеты символьной математики (Mathematica, Matllab, Maple), которые позволяют решать сложные задачи, не задумываясь об их устройстве и не владея математикой (но хорошо владея профильным софтом).
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал