garch

Результат GARCH фиттинга по 250 акциям, с использованием StudentT в качестве распред ошибки.





Степень хвоста это степень свободы в StudentT, df или ν. Для каждой акции сделан отдельный фитинг, со своей степенью. Цвет историческая волатильность, походу историческая волатильность не влияет на степень, низко и высоко волатильные идут вперемешку.

На удивление разброс большой я ожидал меньше. Насколько достоверно? По идее достаточно достоверно, по каждой акции 50 лет истории или 13тыщ торговых дней, для достаточно точного определения степени хвоста достаточно 5 тыщ точек, а здесь почти втрое больше.

Классический гарч, фиксирует среднее в лог пространстве


Вместо этого он должен фиксировать среднее в линейном пространстве, выражение 𝑙𝑜𝑔𝐸[𝑒^𝑟] должно быть константой.



( Читать дальше )

GARCH и его вариации — измерение краткосрочной волатильности, и продолжение ее в будущее, что то вроде EWA. Простой, понятный, быстрый. Вроде работает неплохо для 1 дня, но мне кажется что для больших сроков предсказаний работает не очень.

HAR — комбинация кратковременной и долговременной меры волатильности. Простой, понятный, быстрый. То что я использую и мне кажется наилучший из простых подходов. Работает и для 1д и для больших сроков и мне кажется более надежен чем GARCH.

SV — эволюция GARCH добавлена неопределенность, по сути это Байесовский Гарч. Выдает не просто предсказание вооатильности как число, но распределение вероятности для волатильности. Медленный, тяжелый алгоритм, сложный. Мне кажется как и Гарч не подходит для больших сроков предсказаний.

И я думаю SV позволяед точнее чем Гарч, симуляцикй монье карло сгенерировать процесы цен, и например посчитать опционы, или построить распред вероятн на любую дату в будущем.

SV-RV — тоже самое что SV но позволяет вносить уточняющие данные, например интрадей волатильность.

( Читать дальше )

Н. Талеб упомнал что при тяжелых хвостах 3 (именно такие у дневных цен) Var[Var] равен бесконечности.

Это значит огромные ошибки измерения Var (очень медленное схождение) и неприменимость GARCH и т.п.

Я в прошлом посте упустил что GARCH измеряет условную волатильность а не i.i.d, и ее сходимость может быть совершенно другая, быстрее и стабильнее, чем сходимость i.i.d.

Итог — походу GARCH с Variance использовать можно, или как вариант можно использовать GARCH с MeanAbsDev (она имеет очень быструю и стабильную сходимость, но, менее чувствительна к всплескам). Что лучше — непонятно, вопрос оставляем открытым.

Эксперимент измерение сходимости Var для i.i.d. ь действительно как видим медленная и нестабильная, но как сказал для реальных цен ситуация мож быть гораздо лучше

GARCH предсказывает волатильность на след день как линейную комбинацию текущей и долгосрочной меры волатильности.


И разные варианты GARCH отличаются в основном лишь тем как измеряются эти две компоненты. Т.е. вся идея GARCH строится на измерении текущей и прошлой волатильности как variance.

Теперь возвращаемся к критике Талеба — что дисперсию (variance) нельзя точно измерить (см прошлый пост).

Симуляция показывает, что при экспоненте хвостов ~3 для боль менее точного измерения волатильности — нужен сэмпл размера где то 50-300.

Учитывая что GARCH меряет долгосрочную волатильность как EWA (что по сути уменьшает размер сэмпла раз в 2-3) плюс огромный вес одной точке — текущей волатильности. 

Получается — эти измерения имеют огромный разброс (variance of variance). И соотв. точность GARCH, даже скорей принципиальная обоснованность его использования — под вопросом.

Перефразируя — variance при хвостах 3 имеет медленную сходимость, и ее точечное измерение с свысокой точностью не получится.

Почти нет постов про GARCH на СмартЛабе…

Дневные левый 3, правый 3.7.
Месячные левый 3, правый 5.2 (но я думаю он тоже 3.7, просто данных меньше и его не видно).

Это значит SkewStudentT(𝜇,𝜎,𝜈,𝜆) может быть не достаточно, если мы зафиксируем nu=3, это переоценит вероятность редких положит событий, и хотя сама по себе ошибка может быть малой, тот факт что это экстремальное событие большого масштаба, да еще и в экспоненте exp(log r) увеличит ошибку.

В идеале конечно надо что то типа SkewStudentT(𝜇,𝜎,𝜈𝑙,𝜈𝑟,𝜆) с разными хвостами, но таких вроде как нет.

Либо, зафиксировать nu=3.7, это недооценит убытки, но зато ошибка не будет увеличиваться большим масштабом события.

Добавлено:

Ошибка (относителная) для VaR, портфель из 10 акций и события раз в 10 лет, при хвосте 3 и 3.7. Дневные: ~1.22 раза, месячные: ~1.24 раза. Вполне ощутимая разница.

# Daily, typical daily log returns StudentT(0.001, 0.015)
p = 1-1/(365*10*10) # once in 10y for portfolio of 10 stocks
exp(
  quantile(StudentT(0.001, 0.015, 3), p) - 
  quantile(StudentT(0.001, 0.015, 3.7), p)
) # => 1.22

# Monthly, typical monthly log returns StudentT(0.01, 0.08)
p = 1-1/(12*10*10) # once in 10y for portfolio of 10 stocks
exp(
  quantile(StudentT(0.01, 0.08, 3), p) - 
  quantile(StudentT(0.01, 0.08, 3.7), p)
) # => 1.24

Получается неверный результат если есть ассиметричность, настоящее значение 4, но он неверно определяет как 3 для левого и 5 дле правого хвоста. Или, скорей дело не в Hill а само распределение искажает хвосты? Никто не сталкивался? код



На графике две линии должны стабилизироваться на отметке 4, а они показывают 3 и 5.

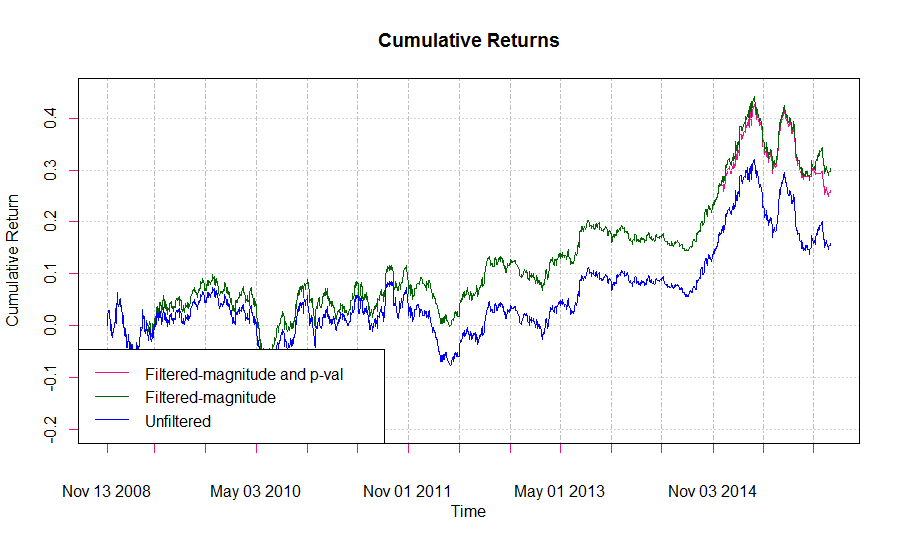
Продолжение. Начало здесь.

Вы, наверное, заметили, что в процедуре вычисления параметров модели, описанной выше, я запоминал действительные предсказанные значения, так же как и предсказания направления приращения цены. Я хочу исследовать предсказательную способность величины  приращения. Точнее, может ли фильтрация сделок, в случаях, когда величина предсказанного приращения ниже определенного порога, улучшить доходность стратегии? Код ниже представляет такой анализ для небольших порогах приращений. Для упрощения, я конвертировал логарифмы приращений в простые приращения, чтобы получить управление знаком предсказания и облегчения применения порога:

# Test entering a trade only when prediction exceeds a threshold magnitude
simp.forecasts <- exp(ag.forecasts) - 1
threshold <- 0.000025
ag.threshold <- ifelse(simp.forecasts > threshold, 1, ifelse(simp.forecasts < -threshold, -1, 0))
ag.threshold.returns <- ag.threshold * returns[(window.length):length(returns)]
ag.threshold.returns[1] <- 0 # remove NA
ag.threshold.curve <- log(cumprod( 1 + ag.threshold.returns))
both.curves <- cbind(ag.threshold.curve, buy.hold.curve)
names(both.curves) <- c("Strategy returns", "Buy and hold returns")

# plot both curves together
plot(x = both.curves[,"Strategy returns"], xlab = "Time", ylab = "Cumulative Return",
     main = "Cumulative Returns",  major.ticks= "quarters", #
     minor.ticks = FALSE, ylim = c(-0.2, 0.45), col = "darkorange")
lines(x = both.curves[,"Buy and hold returns"], col = "blue")
legend(x = 'bottomleft', legend = c("Strategy", "B&H"),
       lty = 1, col = myColors)

( Читать дальше )