SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Quik
Новая версия Рабочего места QUIK — 7.10
- 28 марта 2017, 09:57
- |

arqatech.com/ru/about/news/quik-7-10/
Цифры — шок:
Среди других нововведений версии следует отметить увеличение количества сохраняемых «свечек» графиков в локальном хранилище Рабочего места с 3000 до 65000.
Если ранее к тестированию в QUIK можно было относиться как к забаве, то теперь это становится уже интересным делом!
Скачивайте, тестируйте. Будут вопросы — пишите.
Trend is your friend...
- 15 марта 2017, 21:45
- |
Главное что бы тренд, был настоящим другом, а не лосём в маске.
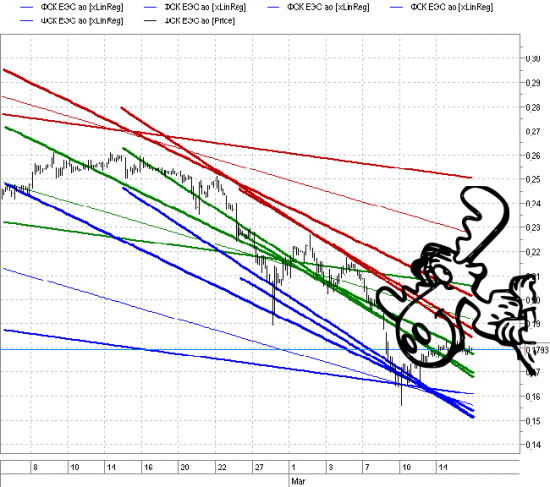
Пока сам рисуешь, и рука дрожит и глаз замыливается, и есть уже отпечаток в мозгах желаемого направления из-за давящей позы или сладкопоющего пиарщика/аналитика)))
Отрисовка просто линейной (и прочих) регрессии тоже не спасает, рисуется красиво, но всё равно период не знаешь, и подгоняешь под хотелки.
Пришлось пойти творческим научным методом ;-)))
( Читать дальше )
Нужна помощь
- 10 марта 2017, 19:00
- |
Сегодня до 16-00 работал в терминале без проблем, потом на 2 часа ушел из дома, при повторном запуске quika вылезла ошибка!
Подскажите кто с таким сталкивался как устранить ошибку?
Подскажите кто с таким сталкивался как устранить ошибку?

Можно ли в Quik задать окно,куда бы выводились лидеры роста и падения за текущую торговую сессию?
- 22 февраля 2017, 16:42
- |
В таблице заявок Quik (7.5) по некоторым исполненным заявкам на forts есть 'Код биржи', а по некоторым нет. Это означает, что исполненная заявка не попала на биржу, а заключена с брокером?)
- 21 февраля 2017, 15:49
- |
- ответить
- 100 |
- Ответы ( 0 )
Привязка окон в Quik
- 20 февраля 2017, 00:40
- |
В Quik (не знаю с какой версии, у меня 7.5.0.72) появилась возможность делать привязку окон. Что-то на подобии привязки к группе, как это сделано в тосе, авроре, арче...
Очень полезная фича, что заметно ускоряет анализ.
Делается это просто:
1. Создаем вкладку
2. Добавляем окно «Текущие торги» и все остальные необходимые окна
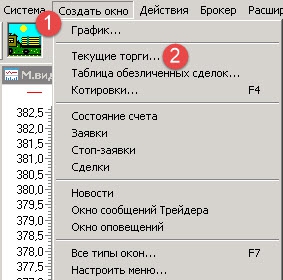
( Читать дальше )
Очень полезная фича, что заметно ускоряет анализ.
Делается это просто:
1. Создаем вкладку

2. Добавляем окно «Текущие торги» и все остальные необходимые окна

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал