прогнозирование

Я уже писал о попытке применить нейросети, и вердикт был неутешительным, с точки зрения практического трейдинга. Я усердно (более менее) прокачивал свои скилы в машинном обучении, учился программировать, в качестве данных используя котировочки, но особой перспективы не видел. Но я оказался не прав, и в конечном итоге, у меня в нейросеть на фондовом рынке получилось.   
Но давайте не сразу к прогнозированию и зарабатыванию денег, сначала рассмотрим другой вариант практического применения нейросетей. 
Нейросеть как черный ящик.
Допустим есть у вас рабочий алгоритм, который показал свою эффективность на протяжении 10 лет реальной торговли. Вопрос как его продать, не раскрывая секреты трейдерской кухни? А почему бы не использовать неинтерпретируемость нейросетей, превратив ее слабости в ее силу? Эта мысль приходила мне раньше, но реализация подкачала, до ума эту мысль я довел недавно, благо потребность возникла. Схема очень простая, у нас есть сырой ряд, из которого нужно посчитать нужные признаки (признаки это и есть мои трейдерские секретики), эти признаки настолько хороши, что подав их в простенькую модель машинного обучения мы получим хороший результат. Но как скрыть алгоритм расчета признаков? А все просто, мы на вход в нейросеть подаем котировочки, а на выход в качестве таргета — наши секретные признаки, таким образом поставив перед нейросетью задачу калькулятора. Подчеркну, тут мы ничего не прогнозируем, признаки находится внутри временного ряда. Это первый этап. На втором этапе мы занимаемся уже прогнозированием, используя полученные признаки. 

( Читать дальше )

Технический анализ один из самых популярных методов в попытке спрогнозировать цену финансовых активов, или же найти наиболее вероятную точку для входа/выхода в/из них. По нему написано масса книг, придумано огромное количество индикаторов и еще больше объяснений как ими пользоваться. Конечно, определенная простота методов ТА не может не привлекать людей, а смотря как он ведет себя на истории, у многих создается реальное впечатление, что ТА обладает некоторой предсказательной силой.

Взглянув на следующий график котировок, даже без методов технического анализа, создается впечатление, что перед нами интересные акции, у которых есть постоянный рост. За 5 лет она выросла в 2,86 раза, что эквивалентно 30% годовых, если считать по методу сложного процента.

Технические аналитики или инвесторы, размышляя над тем, стоит ли купить данную акцию или продать ее (например, в шорт), конечно нанесут на данный график индикаторы, уровни и все те методы, которые они используют и интерпретируют для себя как сигналы в принятии решений. Выглядеть это может по-разному, например так как показано на следующем графике. В любом случае по итогу этих построений, кто-то увидит хороший момент покупки, кто-то хороший момент для продажи, а кто-то решит, что еще не пришло время ни для одного ни для другого.

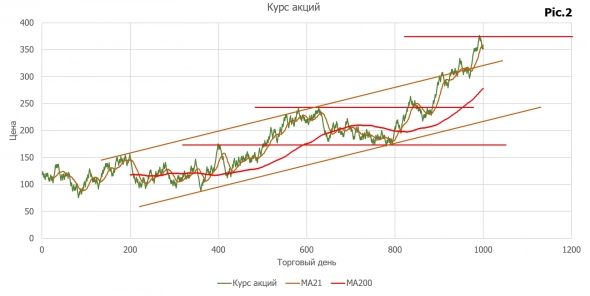
( Читать дальше )

Итак, код обучения и прогнозирования нейросетью рыночных котировок на 5 минут.

import sqlite3 as sql
from scipy.stats import logistic
import math
import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor

sdata =[]
sql1= "select ticker, date, open, high, low, close, vol \
    from Hist_1m where ticker_id=1 order by Date;"
con=sql.connect('C:/Users/ubase/Documents/StockDB/StockDB21.sqlite')
cur=con.cursor()
cur.execute(sql1)
sdata=cur.fetchall()
con.commit()
con.close()

Ldata = len(sdata)
N = 8000 # Количество сделок
ld = 5 #Продолжительность сделки
NNinterval = 20 # Количество входов NN

# Генерация случайных чисел
rng = rnd.default_rng()
rm=rng.integers(0, Ldata, N )

class Candle:
    tr = 0
    dt = 1
    o = 2
    h = 3
    l = 4
    c = 5
    v = 6
    
cl = Candle
DataC =[sdata[i][cl.c] for i in range(0,Ldata)]

# sigmoid линейность до 0.5
def sigmoidnorm(x, alfa = 0.9, xmin = -1.3, xmax = 1.3):
    return (xmax - xmin)*((1 / (1 + math.exp(-x*2.0*alfa))) - 1.0) + xmax

x = [0.002 * i - 3 for i in range(0,3000)]
y = [sigmoidnorm(x[i]) for i in range(len(x))]


plt.plot(x,y)
plt.grid()
plt.show()

# формируем сделки.
def DealsGenL(rm,ld):
   #Lm = len(rm)
   ix = []
   x = []
   pr = []
   
   for i in range(0,N):
        if rm[i] + ld < Ldata and rm[i] - NNinterval - 1 > 0:
            delta = (sdata[rm[i]+ld][cl.c] - sdata[rm[i]][cl.c])/sdata[rm[i]+ld][cl.c]*100
            x0 = [sigmoidnorm((sdata[rm[i] - j][cl.c] - sdata[rm[i]][cl.c])/sdata[rm[i]][cl.c]*100) \
                 for j in range(0, NNinterval)]
            ix.append(rm[i])
            x.append(x0)
            pr.append(delta)
   return ix, x, pr


Ix, X, Pr = DealsGenL(rm,ld)



Ib = 0
Ie = 100

plt.plot(X)
plt.legend()
plt.grid()
plt.show()


plt.plot(Pr, label = 'Prof')
plt.legend()
plt.grid()
plt.show()


regr = MLPRegressor(hidden_layer_sizes = [30,20,15,10,5], \
                    max_iter=500, activation = 'tanh')

regr.fit(X, Pr)
Out = regr.predict(X)

plt.plot(Pr, Out, '.')
plt.grid()
plt.show()

И вот результат прогнозирования:

( Читать дальше )

Был у меня на днях диалог с одним нашим форумчанином, и сказал он с некоторым сожалением — через 5 минут прогноз рассыпается. ©
Вообще, я с этим вполне согласен, это действительно близко к истине. Однако,
во первых: 5-ти минут часто вполне достаточно для сделки,
во вторых: по ходу пьесы можно прогнозировать и дальше, на следующие 5 минут, и, если все ОК, продлевать сделку на следующие 5 минут, потом на следующие и так далее.
Таким образом, мы поимеем систему, в которой, да, основные сделки будут не более 5 минут, но будут присутствовать и сделки более продолжительные, до 15 минут и более.
Только скажу, что из этого может получиться оч неплохая и весьма прибыльная система.

Основной вопрос — может ли НС, и вообще методы МО, прогнозировать рынок?
Зададим более простой вопрос — можно ли НС обучить выполнять оператор if()… else? Ответ очевиден — конечно можно.
А обучить выполнению группы таких операторов? — Не вопрос, конечно можно.
Т.е., НС можно обучить практически любой логике. Вроде, сомнений не вызывает.

Теперь у нас есть заведомо работоспособная прибыльная торговая система (ТС), принимающая решения о покупке/продаже на основе некоторых данных, констант и логики. Решение — это своего рода прогноз. Решение: покупать — это прогноз роста цены актива, продавать — прогноз падения цены.

Итак, если ТС построена на логике, а НС можно успешно обучить любой логике, то НС можно обучить логике нашей прибыльной ТС. А так как решение ТС — это прогнозирование рынка, то НС и другие методы МО без всяких сомнений могут прогнозировать рынок.
Вот, мы с вами все и доказали:
НС и другие методы МО без всяких сомнений могут прогнозировать рынок.

Думай медленно — предсказывай точно. Искусство и наука предвидеть опасность. ФилипТетлок, ДэнГарднер

Электронная книга https://t.me/kudaidem/1808

Часть 1 https://smart-lab.ru/blog/673858.php Часть 2 https://smart-lab.ru/blog/674129.php

( Читать дальше )

Думай медленно — предсказывай точно. Искусство и наука предвидеть опасность. ФилипТетлок, ДэнГарднер

 Электронная книга https://t.me/kudaidem/1808
Часть 1 https://smart-lab.ru/blog/673858.php

( Читать дальше )

Думай медленно — предсказывай точно. Искусство и наука предвидеть опасность. ФилипТетлок, ДэнГарднер

Электронная книга https://t.me/kudaidem/1808

( Читать дальше )

Глава 2. С чем Россия подошла к пандемии?
Электронная книга t.me/kudaidem/1703

( Читать дальше )

Различных методов Machine Learning очень много, но все они работают примерно одинаково. Это и нейросети, и леса-деревья, и Байесовские классификаторы, и многое другое. Найти и прочитать как ходят-как сдают, как обучают и проверяют правильность обучения — не проблема.
Но пользователи часто забывают одно правило: мусор на входе — мусор на выходе. Для обучения недостаточно сделать обучающую последовательность с правильными ответами — результатом будут хорошие результаты на обучающей последовательности, и никакие на реальных данных.
Таким образом, мы должны четко себе представлять, чему именно мы учим, и это вовсе не правильные ответы, а правильные ответы на правильные вопросы. Если не хотите получать дурацкие ответы — не задавайте дурацкие вопросы.

Т.е., для обучения МЛ нам нужно сформулировать адекватные вопросы и ответы на них. Только в этом случае метод МЛ реально обучится и будет реально работать не только на обучающейся последовательности.
Вопрос ещё в том, что обычно мы не знаем и правильных вопросов.
Но это дело поправимое  Мы формируем какую либо гипотезу, например — три солдата показывают нам то-то и то-то. Мы как-то ищем этих трёх солдат на истории, там же находим ответы на них, обучаем на этом метод МЛ, проверяем на независимом отрезке истории, и выясняем — действительно ли эти 3 солдаты так важны для нашей торговли, или ну их на фиг.
Понятно, что и при обучении и на реале нам надо задавать МЛ только значимые вопросы, а именно, показывать МЛ не все данные подряд, а только наших трёх солдат.
Ну, а если солдаты воевать не желают, проверяем значимость вороны на шесте.) И так, пока действительно не найдем что-то стоящее.