Избранное трейдера suslik
Паттерн ЖО*А, Ловите простой и максимально простой грааль для фьючерсов.
- 11 апреля 2016, 05:54
- |
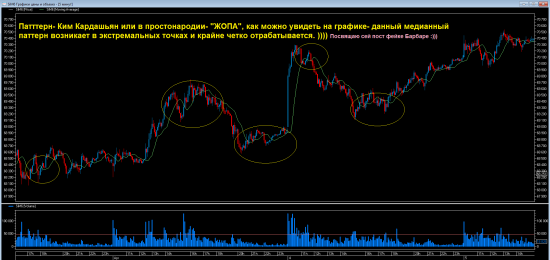
- комментировать
- 61 | ★2
- Комментарии ( 0 )
ФРС объявила сегодня о внеочередном заседании в понедельник 18:30мск
- 08 апреля 2016, 16:44
- |

P.s. Это заседание Совета управляющих, а не Комитета по открытым рынкам (FOMC)
так что возможно ничего важного
Про собеседования и работу
- 06 апреля 2016, 15:47
- |
Скажу сразу, это как отношения с женщинами. Очень много общего. И данную аллегорию я буду использовать часто. :)
1. Уверенность, причем внутренняя уверенность, что в вас нуждаются не меньше чем вы в компании. Отчаяние, страх — все это чувствуется подсознательно. Как обрести эту уверенность — есть несколько вариантов. Самый простой — это наличие существующей работы, откуда вас не увольняют. Вы ничего не теряете на собеседовании! Вы пришли проверить рынок, посмотреть. Похожее ощущение дают альтернативные офферы. Основной драйвер уверенности — ваше чувство собственной компетенции. Когда я приходил 10 лет назад на аналитика, имея два сданных уровня CFA, и меня спрашивали, могу ли я пройти тест сделанный по 1му уровню — я улыбался, и понимал, что заведомо превышаю то, что нужно компании.
2. Подготовка. Вам нужно постараться выяснить, что хочет компания. Какие ключевые компетенции от вас ждут. Вообще, подготовка — это очень важно. Проявляя знания о менеджменте, собственнике, чем занимается компания, какие-то ключевые проекты — вы производите хорошее впечатление. Худшее, что можно сделать — это быть человеком, который пришел просто потому что ходит по разным квази-подходящим вакансиям. Работодатель — это как женщина. Вам нужно показать, что вы именно ее хотите, и полунамеками объяснить почему.
( Читать дальше )
Про алгоритмы в режиме 2х2
- 05 апреля 2016, 02:23
- |
1. Книга открывает мир алгоритмов с другой стороны. Больше никаких сложностей. Это как переход от командной строки линукса в последнюю оболочку MacOS. Даже круче, и шаг шире. Если до сих пор алгоритмы были привилегией математиков и программистов, то после ее прочтения сложный торговый алгоритм может составить даже семиклассник или пожилая домохозяйка. С двадцатой страницы хочется взять ручку и бумагу, чтобы нарисовать алгоритм.
Большое внимание уделено эргономике алгоритмов. Причем, эта эргономика четко описана и подчиняется весьма квадратным правилам. Никаких разночтений. Вероятность ошибки сведена к значениям после запятой.
2. В книге описан графический язык ДРАКОН, который придуман российскими учеными при проектировании Бурана. Расшифровывается название языка как «Дружелюбный Русский Алгоритмический, Который Обеспечивает Наглядность». Язык ДРАКОН был разработан, в частности, потому, что традиционные блок-схемы алгоритмов, с эргономической точки зрения, не выдерживают критики. Они напоминают непроходимые джунгли, в которых легко запутаться и почти ничего нельзя понять.
( Читать дальше )
Задача о котировке, которая никогда не вернется
- 28 марта 2016, 11:12
- |
Большинство трейдеров знают важное правило биржевой игры: если ты купил акцию, а она подешевела, то не спеши её продавать. Скорее всего, она рано или поздно вернётся на былую позицию, да ещё и пойдёт вверх. Вопрос лишь в том, когда это произойдёт. Очень часто трейдер ждёт месяц, год, десять лет — а цена акции “на место” не возвращается. Вроде бы и фирма не банкрот, и кризисов особых нет — но котировка как когда-то просела, так и “толчётся” недалеко от цены покупки. И скачет по всякому, а возвращаться не хочет. Как будто специально, чтобы тебе “насолить”. Но злого умысла тут нет, а есть очередной парадокс теории игр.
( Читать дальше )
Как в ВТБ24 получить двойную комиссию при работе с плечом
- 23 марта 2016, 11:37
- |
Каково же было моё удивление, когда я обнаружил за прошлый четверг сделки РЕПО на 440 тысяч рублей! То есть, брокер продал моих акций не на 120, а на 220 тысяч, а на следующий день утром их выкупил, ночью у меня было 96-98 тысяч рублей кеша. Ну и, соответственно, комиссия в два раза больше, чем я ожидал — 125 рублей (за сами сделки РЕПО и за то, что брал взаймы), это 0.1% от суммы долга или 36.5% годовых. Не много ли? Почему брокер «одолжил» мне денег в два раза больше, чем требовалось?
Начал разбираться, в сделки РЕПО попали Уралкалий, Северсталь, Лукойл и Транснефть (одна акция), тогда как одной акции ТН было бы достаточно, чтобы перекрыть весь мой долг. Мало того, можно было бы вообще не продавать Транснефть, а закрыть мой долг брокеру другими, менее дорогими акциями. Зачем было брать самую дорогую акцию — ТН, которая стоит в 1.5 раза больше долга? А главное, зачем было добавлять к ней другие акции?
( Читать дальше )
Кому грааль, или вечные опционы без временного распада.
- 21 марта 2016, 12:17
- |
Все наверняка в курсе о достоинствах и недостатках покупки классического(ванильного) опциона перед покупкой инструмента(Базисного Актива, БА) на который он выписан.
Если в кратце, то:
Плюсы в том, что если мы купили опцион(допустим за 1000) и цена БА пошла в нашу сторону(тут и далее я говорю об опционах без денег), цена опциона может вырасти скажем в 5 раз и более( увеличиться до 5000+)… а если против нас — уменьшится в 5 раз и более (уменьшится до 200 и менее). По сравнению с покупкой БА мы потенциально неограниченную возможную прибыль при ограниченном риске. К тому же с опционом мы можем не бояться, что страшный гэп по БА в понедельник с утра обнулит наш счет и мы останемся еще и должны брокеру(многие не воспринимают эту опасность всерьез, но для долгожителей на рынке это едва ли не самый страшный из рисков)...
Вышеописанные ништяки в целом почти полностью нивелируются временным распадом опциона — если БА не движется в нашу сторону, то временная стоимость опциона «испаряется».
А существует ли инструмент ведущий себя как опцион, но без временного распада? Вопрос на первый взгляд весьма идиотский, и у многих на языке уже вертится что таких инструментов существовать не может в принципе потому что free launch theorem и всё такое, т.д. и т.п...
Но сегодня утром я внезапно понял что такие инструменты на практике существуют! Это [дешевые] акции.
Рассмотрим какую-нить [дешевую] акцию n-го эшелона. Скажем GTL
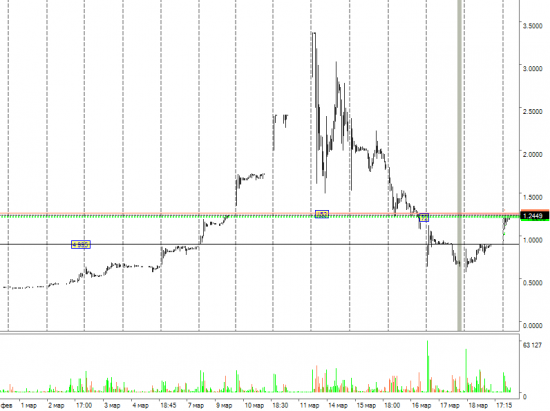
( Читать дальше )
Controlled Checkered robot - Управляемый Клетчатый Робот
- 16 марта 2016, 16:20
- |
http://smart-lab.ru/blog/313792.php
http://smart-lab.ru/blog/314938.php
http://smart-lab.ru/blog/315291.php
Управление размером позиции
Бинарную матрицу набора результатов работы роботов можно использовать для управления размером позиции при торговле. Подход очень простой – сумме единиц в матрице приводим в соответствие размер позиции.
Попробуем этот интуитивно понятный подход выразить формулами.
Берём квадратную матрицу размера 3х3 с набором бинарных «мнений» роботов.
Aij= 
Где aji – «мнение» отдельного робота.
Назовём такую матрицу клетчатым роботом (checkered robot).
Графически клетчатый робот выглядит как матрица квадратиков разного цвета.
( Читать дальше )
Брокеры и клиенты: статистика НАУФОР
- 02 марта 2016, 15:03
- |
Количество новых клиентов для открытия ИИС составило 55 тыс чел
Средний размер счета ИИС: 260 тыс рублей.
Средний размер счета доверительного управления — 160 тыс. руб.
Общий объем средств, переданных брокерам и управляющим = 420 млрд рублей.
Общий объем средств граждан на рынке = более 500 млрд рублей
сред. р-р брокерского счета = 150 тыс рублей.
сред. р-р счета доверит управления = 450 тыс рублей
где размещены деньги клиентов?
32% — акции российских эмитентов
19% — кэш
18% — еврооблигации
2,3% — российские корп. облигации
0,6% — ПИФы
Источник инфы: http://fomag.ru/ru/news/stocks.aspx?news=9958
Лучше чем грааль - чему меня научили опционы
- 01 марта 2016, 21:26
- |
Итак, опционы научили меня простым вещам, отчасти граалю, которые применивы точно так же и в линейном трейдинге:
1. Не прогнозируй куда пойдет цена — так ты просто накладываешь свое осознанное или не осознанное желание на реальность и результатом лишь твое искаженное ее восприятие и без вариантов ты за это поплатишься. Вместо этого определи куда цена пойдет вероятнее всего в рамках рассматриваемого промежутка времени! В опционах можно просто посмотреть на дельту определенного страйка и она покажет с определенной погрешностью вероятность того, что цена дойдет к эскпирации к этому страйку. Дельта 0.1 означает примерно 10% вероятность. В линейном трейдинге можно оперировать линиями поддержки и сопротивления, каналами, от которых уже была четкая реакция, торговым диапазоном. Если цена в диапазоне — вероятнее всего она там и останется. Если в тренде — вероятнее всего он продолжится. Если пилит стопы — вероятнее всего так и будет. Не нужно ожидать, что что-то изменится. Нужно лишь иметь план на этот случай. Изменится — нужно рассмотреть новую ситуацию и вероятности.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
