Избранное трейдера Игорь
Опционы по взрослому (календарный спред).
- 16 марта 2017, 12:34
- |
Вообще это самая простая тема. Мне придется ссылаться на календарные позиции в дальнейших рассуждениях, поэтому я об этом пишу. Это скорее общеобразовательное повествование. Поэтому гуру прошу не пинать, а для постигающих опционный мир это должно быть интересно.
Волатильность входит в стоимость опциона через время. То есть там такое выражение в d1 сигма*корень из времени до экспирации. И если времени у нас осталось мало, близко к нулю, то и волатильность уже не играет роли и наоборот. Поэтому попробуем посмотреть на эти опционы через жопу желтые очки. Представьте себе, как исторически могло сложиться в прайсинге опционов. Не стали бы трогать волатильность. Ну есть БА, у него есть вола, пусть себе болтается. Делаем ее константой. Тогда опционы нужно было бы оценивать в днях до экспирации. При этом мы бы продавали опцион, который исполнится через 30 дней, по цене 40 дневного опциона. 10 дней ложились бы к нам бонусом. И спред бы у нас считался в долях дня. Мы ведь считаем дюрацию облигаций, используя дни? А почему не посмотреть на опционы под тем же углом. Тем более в календарном спреде у нас один БА с одной волатильностью. Я составил табличку
( Читать дальше )
- комментировать
- 1.6К | ★24
- Комментарии ( 80 )
Дорогие ОПЦИОНЫ ))))
- 16 марта 2017, 12:05
- |
Вот где идет в опу — блек и шоилс )))) ну а для нас вопрос для размышления )))
Анализ спроса и предложения (робот)
- 16 марта 2017, 11:57
- |
В КВИКе есть такие поля:
Суммарный спрос — количество лотов, выставленное на покупку (даже за пределами видимости стакана)
Суммарное предложение — количество лотов, выставленное на продажу (даже за пределами видимости стакана)
Количество заявок на покупку — сколько люди, звери, птицы и юр.лица поставили заявок на покупку (даже самых маленьких — однолотовых)
Количество заявок на продажу — сколько заявок выставлено на продажу.
Вот они.
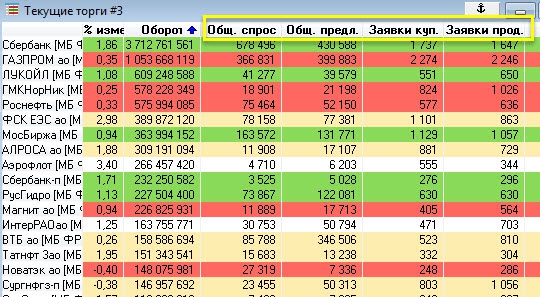
Полезность этих полей можно критиковать. Мол, они не показывают айсберги, крупный игрок может умышленно поставить большой пакет вдали от рынка, однолотовые заявки искажают картинку… Это всё так, и я не защищаю этот метод анализа.
Тем не менее, я написал робота, который эти параметры анализирует. Робот только что из печки, горяченький.
( Читать дальше )
Робот ContanGO!
- 10 марта 2017, 16:35
- |
Я написал простенького робота, который считает контанго и бэквордацию между фьючерсом и акцией.
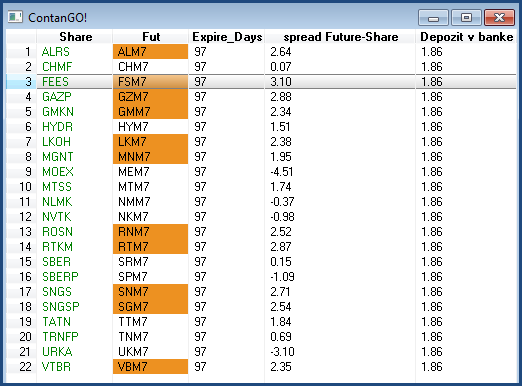
Значения полей:
Share — акция, базовый актив
Fut — фьючерс на эту акцию
Expire_Days - сколько дней до экспирации
spread Future-Share — размер контанго или бэквордации, то есть разница между ценой фьючерса и базового актива
( Читать дальше )
QUIK - перезагрузка
- 17 февраля 2017, 14:23
- |
У меня возникла острая необходимость заниматься диверсификацией портфеля, но как бы не был популярен QUIK, его ограниченные возможности не позволяют проводить анализ и выборку сразу по множеству инструментов — только индикаторы и только на одном графике. Пока втыкаешь в один вялый инструмент, рядом протекает активная жизнь. А в Excel - уже порядком поднадоело + не онлайн.
СТРАТЕГИЯ
Решил расширить возможности QUIK.
ТАКТИКА
— для начала сделал базовый-модуль:
[подключение к QUIK]
[получение текущих данных]
[закачка исторических данных]
[расчёт корреляций по всем акциям РФР+индексы]
АНАРХИЯ и HOLYWAR
Решением делюсь, т.к. заядлых Квикеров много, а софта мало, особенно заточенного под инвестора, а не под алго-HFT-дрочеров.
СКРИНШОТ
( Читать дальше )
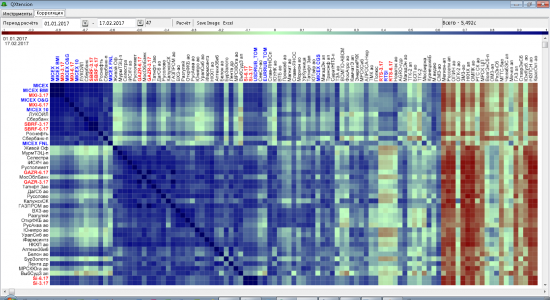
Корреляция РФР 2017.
- 16 февраля 2017, 12:35
- |
Корреляционная кластерная карта Российского рынка акций с начала 2017 года.
(в помощь ищущим чем бы задиверсифицироваться)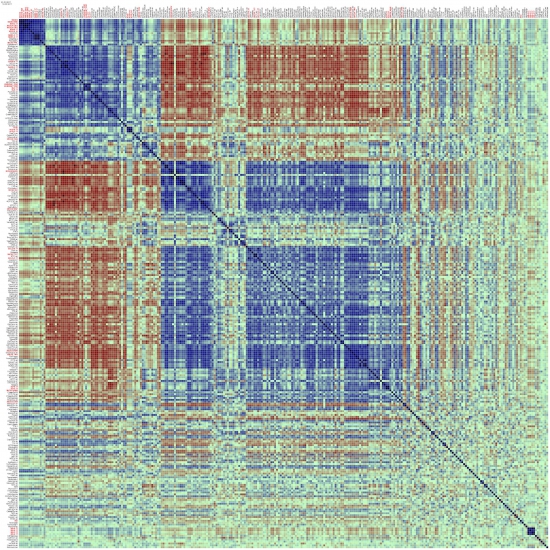

( Читать дальше )
СОТ-репорты. Кто обыгрывает рынок?
- 14 февраля 2017, 21:14
- |
Что скрывают знаменитые СОТ-репорты? Какие группы игроков наиболее успешны и стоит ли частному инвестору копировать их действия? Благодаря чему достигается положительный результат и насколько он устойчивый? Каковы особенности поведения производителей, своп-дилеров и хедж-фондов? Какова разница между товарными и валютными рынками и есть ли вообще единые правила анализа СОТ?
Чтобы ответить на эти вопросы, придётся создавать специфическую расчётную модель, но прежде надо установить объективные критерии, которые характеризуют поведение той или иной группы игроков. В первую очередь, это средняя чистая позиция (лонг минус шорт) за всё время наблюдения (с 2006-го по 2016-ый годы), а также коэффициент корреляции между приращением чистой позиции и приращением логарифма цены (на интервале 4 недели). Рассмотрим их на примере золота (таблица 1).

( Читать дальше )
Улыбка волатильности в ITInvest, нужна помощь.
- 01 февраля 2017, 12:10
- |
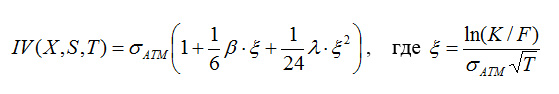
Наверное все видели эту формулу на сайте ITInvest http://www.itinvest.ru/software/smartx/trade-option/ulibka-volatilnosti/ в презентациях Олега Мубаракшина, в лекциях Владимира Твардовского и на Великой Китайской стене в Поднебесной. Напомню, бетта это 3-й момент распределения, лямбда это 4-й момент. Я плохо разбираюсь в математике, но со слов, которым доверяю, слышал, что 1/6 и 1/24 это константы, которые позволяют думать об бете и лямбде как о кумулянтах или полуинвариантах или даже как о семиинвариантах. И вот, готовя очередной топик, я столкнулся с такой фигней, что уважаемый мной ITInvest использует другую формулу. Вместо 1/6 у них 4, а вместо 1/24 у них 12. Возник вопрос, на который я попытался найти ответ через личную переписку, но ничего… Поэтому прошу помощь клуба. Буду очень признателен если кто нибудь разъяснит мне этот феномен.
Технический индикатор РТС на основе данных MOEX и USD/RUB
- 29 января 2017, 18:59
- |
Недавно, были дебаты Опционного математика и Опционного не математика по поводу:
«Нужна ли математика в опционной торговле» каждый наверное сделал свой вывод.
Я приведу пример, как использовать элементарную математику в прогнозировании стоимости РТС, не глядя даже на его график.
Нам нужен график доллар/рубль и график ММВБ
Давайте назовем функцией Y(t) — график USD/RUB, а график ММВБ — X(t)
Таким образом, всегда будет выполнятся равенство Y(t) = A*X(t) + B
Наша задача найти B — это и есть ошибка(отклонение) двух функций.
Для начала находим А:
Возьмем ограниченный период 5-ти ближайших торговых дней.
Имеем y(t)1 и y(t)5, x(t)1 и x(t)5
Используя знания о геометрическом свойстве Интеграла:
Проинтегрируем функцию Y(t) от y(t)1 до y(t)5
Проинтегрируем функцию X(t) от x(t)1 до x(t)5
A = Интеграл Y(t) от y(t)1 до y(t)5 / Интеграл X(t) от
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал