Избранное трейдера Hz
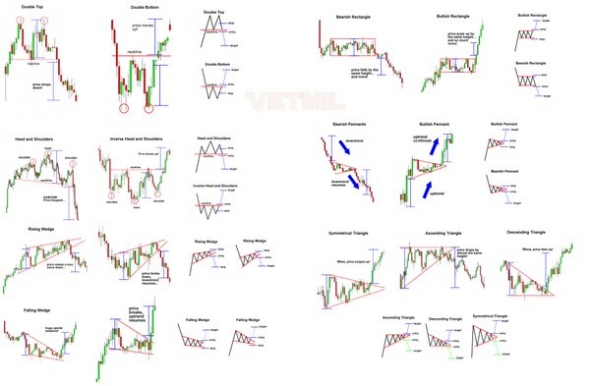
Комплексное руководство по торговле. Паттерны.
- 19 января 2019, 23:46
- |
Т.е. если пинбар маленький, допустим вся свеча на 10-20п по теням свечи, то верность сигнала такая же мизерная. Кроме того, есть такая фишка как достоверность сигнала. В двух словах это значит, что чем дольше по времени свеча рисуется, тем вероятнее последующее ожидаемое движение. И связана это в первую очередь с объемом вовлеченных участников. Чем крупнее сайз — тем сложнее его разобрать и повернуть в спять. Потому торговля старших ТФ точнее отрабатывает сигналы, и имеет меньшее воздействие внутредневного шума и новостей. Я например люблю торговать дневки и недельки и очень редко просматриваю Н4.
( Читать дальше )
- комментировать
- 6.6К | ★52
- Комментарии ( 17 )
Библиотека начинающего инвестора в акции (личный опыт)
- 16 января 2019, 09:27
- |
Приведенная литература примерно на год чтения.
Рекомендую читать в указанном порядке (многие книги есть в свободном доступе в сети):
Мотивационно-популярное:
— Джордж Клейсон. «Самый богатый человек в Вавилоне»
https://bookz.ru/authors/djorj-kleison/samii-bo_574/1-samii-bo_574.html
— Роберт Кийосаки. «Богатый папа, бедный папа»
https://www.litmir.me/br/?b=259942&p=1
— УК «Арсагера». «Какой смысл покупать акции?» (ЧИТАТЬ ОБЯЗАТЕЛЬНО)
arsagera.ru/kuda_i_kak_investirovat/zachem_nam_fr/kakoj_smysl_pokupat_akcii/
— Дэвид Смит. «Капитал Маркса в комиксах» (ЧИТАТЬ ОБЯЗАТЕЛЬНО)
https://www.labirint.ru/books/565293/
( Читать дальше )
Перезаход внутри позиции ШОРТ
- 11 декабря 2018, 15:58
- |
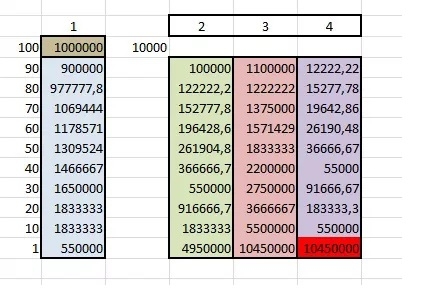
Если Вы были не в курсе этой таблицы, если Вы никогда не задумывались как правильно шортить и почему нужно перезаходить, то Вы от трейдинга очень далеко.
Из Таблицы видно:
Столбик 1. Сумма закрытия шорта на каждом этапе.
Столбик 2. Прирост прибыли на каждом этапе.
Столбик 3. Сумма депозита после каждого этапа.
Столбик 4. Количество акций в Шорте, после каждого этапа.
Как видим в красной ячейке аж 10 млн 450 тыс акций, которые вы можете иметь в шорте на последнем этапе, против 10 тыс на первом, что аж в ТЫСЯЧУ раз больше. Но, лучше конечно на последнем этапе… их купить в ЛОНГ.
( Читать дальше )
Торговая система BWS
- 04 декабря 2018, 07:40
- |
Торговая система BWS
Введение
В основе человеческой психологии лежит желание купить то, что подешевело, то, что стоило раньше 100, а сейчас, к примеру, 90. Подобные сделки кажутся очень выгодными, тем более, что в обычной повседневной жизни они, как правило, действительно являются выгодными. Например, выгодно покупать продукты по акциям в магазине со скидкой, выгодно отовариваться на распродажах, покупать товары при ликвидации магазинов и т.д. Именно поэтому многие и на фондовом рынке придерживаются такой же стратегии, покупая акции компаний аутсайдеров, которые падают и, зачастую, падают сильно. Не скрою, что когда-то и я так торговал, но анализ собственных сделок, а также анализ движения цен на акции лидеров рынка и аутсайдеров, заставили меня пересмотреть этот подход.
Если вы уже давно торгуете на фондовом рынке, то наверняка заметили, что одни и те же бумаги растут сильнее рынка, а другие все время стоят на месте или даже падают. Примеров можно привести много: это и ВТБ, который разместился на IPO в 2007 году по 13.6 копеек, а сейчас стоит менее 4 копеек, это и Газпром, который когда-то в 2008 году стоил более 300 рублей, а сейчас, спустя 10 лет, стоит в два раза меньше. Да и каждый из вас без труда может привести множество подобных примеров. В то же время есть бумаги, которые выросли за это время в несколько раз, оставаясь лучшими много лет подряд.
( Читать дальше )
- комментировать
- 24.1К |
- Комментарии ( 65 )
Про жизнь), Товарищ прислал.
- 24 ноября 2018, 03:22
- |
*Каменный век*: убиваешь мамонта, тащишь к себе в пещеру.
Наедаешься от пуза, остатки запасаешь впрок. Вдоволь отдыхаешь в пещере. Смотришь на звезды, думаешь о жизни. Хорошенько отдохнув и подъев запасы, вновь идешь охотиться.
*Патриархат*: начинаешь делиться добытым мамонтом с женщиной и детьми.
Поэтому мамонт съедается быстрее, приходится охотиться чаще и больше уставать.
Но взамен в пещере уютно, мамонт уже приготовлен и дети на тебя похожи.
*Подоходный налог*: начинаешь отстегивать 13% от туши мамонта самопровозглашённому хозяину Тундры и на эти 13% ещё чаще и усерднее охотиться, чтобы самому по-прежнему хватало прокормить себя и теперь ещё и семью.
*Инфляция:* мамонт, которого ты запасал впрок, чтобы меньше охотиться и больше отдыхать, теперь начинает подъедаться крысами, иногда на 5…7% в год, иногда на 10…15%, а иногда и полностью. Откладывать уже сложнее, нужно либо много думать как сохранить мамонта или просто непрерывно охотиться без серьезных стратегических запасов.
( Читать дальше )
ЛУЧШИЕ ФИЛЬМЫ О ТРЕЙДИНГЕ!!!!
- 18 ноября 2018, 18:35
- |
ФИЛЬМЫ КОТОРЫЕ ОБЯЗАТЕЛЬНО ДОЛЖЕН ПОСМОТРЕТЬ КАЖДЫЙ ТРЕЙДЕР
Сохраните себе для просмотра! (Не забудте отблагодарить)
1. «Аферист» (Rogue Trader, 1999)
Резюме: Более динамичная британская версия «Wall Street.»
Сюжет: за основу взята реальная история трейдера банка Barings, Ника Лисона, роль которого исполняет Юэн МакГрегор.
2. «Поменяться местами» (Trading Places,1983)
Резюме: Самая веселая комедия об Уолл Стрит.
Сюжет: Слушать рассуждения Эдди Мерфи о фьючерсах и рынках — что может быть смешнее?
3. «Варвары у ворот» (Barbarians At The Gate, 1993)
Резюме: фильм и книга – это классика
Сюжет: выкуп RJR Nabsico за кредитные средства
4. «Уолл Стрит» (Wall Street, 1987)
Резюме: классическая картина об Уолл Стрит.
Сюжет: Изначально, режиссер Оливер Стоун планировал обличить жажду наживы, которая царила на Уолл Стрит в 1980-х. Он даже не подозревал, что фильм станет шедевром в финансовой сфере. Персонаж Майкла Дугласа, Гордон Гекко, отчасти списанный с Майкла Милкена и Ивана Бески, стал всеобщим любимцем.
( Читать дальше )
Волатильность. Не новый подход через задний проход.
- 11 ноября 2018, 17:56
- |
Старинные предания говорят, что так было не всегда. В древние времена, когда густые травы были гораздо забористее, а вершины графиков PL скрывались от взглядов любопытствующих за облаками, пещерные трейдеры иногда пытались подкрасться к волатильности с тыла и осветить слабыми фонариками своих навыков тот самый проход.
( Читать дальше )
Универсальный прогноз на каждый день
- 30 октября 2018, 08:34
- |
--
Вчера рынок закрылся в зеленой/красной зоне. Быки/медведи показали свою слабость, но есть шанс на отскок. При тесте верхней/нижней границы, вчерашнего лоу/хай, стоит присмотреть к покупкам/продажам. Сейчас мы находимся в канале, и приближаемся к его границам. При подходе к границам канала рынок или отскочит, или их пробьет. Так же на старшем таймфрейме образовывается треугольник/вымпел/Параллелограмм/Круг ожидаем, как рынок поведем себя у границ этой фигуры.
Все профитов, Ваш Гуру.
--
О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)
- 16 октября 2018, 16:41
- |
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам. Что такое центральная предельная теорема в ее классическом виде?
Пусть нам дана некоторая сумма большого числа случайных величин Х=х1+…+хN где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.
Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если xi – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал