Сборник статей и видео в которых я рассказываю об обслуживании портфель роботов, которые торгую сам.

Это — про трендовую, неспешную торговлю. Торговлю в которую можно загрузить очень много денег.

Здесь Вы найдёте инструкции по полному циклу тестирования, использования и поддержки трендовых стратегий.
Сами стратегии можно взять от сюда: smart-lab.ru/blog/849558.php

Логика построения торговых стратегий

1 Точки входа. smart-lab.ru/blog/770108.php
2 Точки выхода. smart-lab.ru/blog/771155.php
3 Фильтры. Какие бывают и какими пользуемся smart-lab.ru/blog/tradesignals/791903.php

Логика поиска робастности. Тестирование и оптимизация

1 Классические бэк тесты smart-lab.ru/blog/792251.php
2 Walk-Forwards smart-lab.ru/blog/792716.php
     2.1 Дополнение на ютуб, о рабастности

3 Риски в алго. Что не следует делать smart-lab.ru/blog/793379.php
4 О равномерном распределении объёмов между стратегиями smart-lab.ru/blog/793617.php

( Читать дальше )

В этом году Мосбиржа перешла на ассиметричную модель тарифов, при которой по рыночным заявкам в разы выросла комиссия, а для пассивных заявок комиссия была отменена. Такая модель уже действует на срочном и валютном рынках, а с 1 ноября будет введена и на фондовом.
И вот чтобы не попадать на повышенную комиссию придумали новый тип заявки.

В торговой системе вводится новый тип исполнения заявки по остатку — «только пассивная». Такая заявка будет отклоняться торговой системой во всех случаях, когда при постановке её в очередь заявок может сформироваться хотя бы одна сделка. Таким образом, заявка с признаком «Только пассивная» может являться только заявкой мейкера. Заявка с типом «Только пассивная» должна являться лимитной.

Исполнение заявок нового типа происходит только при появлении в очереди заявок встречной допустимой заявки тейкера, при этом возможно частичное исполнение.

Для заявок типа «Только пассивная» на фондовом рынке предусмотрена следующая логика при проверке на кросс-заявки:

• В очереди находится заявка с признаком «Только пассивная», и затем поступает новая заявка, которая приведет к кросс-сделке:
  • Не установлена опция «Снятие пассивной» — отклоняется новая поступившая заявка
  • Включена опция «Снятие пассивной» — снимается находящаяся в очереди заявка с признаком «Только пассивная», новая заявка встает в очередь заявок.
• В очереди заявок находится заявка, которая может привести к заключению кросс-сделки, и в очередь поступает заявка с признаком «Только пассивная»:
  • Не установлена опция «Снятие пассивной» — поступившая заявка отклоняется по общему правилу признака «Только пассивная»
  • Включена опция «Снятие пассивной» — снимается находящаяся в очереди заявка, новая заявка с признаком «Только пассивная» встает в очередь заявок.

( Читать дальше )

Хотел вечером посмотреть какой- нибудь фильм. Уже было решил какой, но к вечеру забыл какой. Спать еще рано, а что-то делать уже поздно. Напишу что-нибудь относительно полезное для полуночников. Читателям не понравится — удалю. Да и вообще, доступ к Граалям должен быть ограничен как в пространстве, так и во времени.
Сразу скажу, что этот Грааль интуитивно всем известен, но лишь немногие его могут сформулировать. Попробую это сделать за вас.)
Вообще-то, единственная стратегия на рынке, это покупай дешево — продавай дорого. Других стратегий просто не существует. Это еще великий Швагер написал. Уж, не знаю насколько он великий, но с этим можно согласится.) Но вы же любите ссылки на книги по теханализу.)
У нас остается всего один нерешенный вопрос — где дешево, а где дорого.
Открываем ваш любимый инструмент и таймфрейм и видим, что график колеблется вверх-вниз, совершая некие волнообразные движения. Понятно — внизу дешево, вверху дорого. Но, как-то волны какие-то неровные, все разной высоты, но явное впечатление, что колеблются они вокруг некоторого смещающегося центра. Можно даже на глаз провести некую плавную линию этого центра — среднюю линию. А можно и не на глаз, а провести некую, скажем ЕМА, которая будет визуально близка той, которую вы провели на глаз. Мы видим, что в графике уже появилась некая система, и волны теперь в основном колеблются вокруг нашей средней. Понятно — под средней дешево, выше средней дорого. Волнение то усиливается, то стихает.

( Читать дальше )

Доброе утро, коллеги!

Оставлю это здесь для памяти.
Этапы, которые по хорошему должен пройти алготрейдер на пути к дзену.

1. Построение оптимальной маркетной ТС

Маркетная ТС — это торговая система, которая предполагает, что финансовый результат сделки — это разница цен входа и выхода. Самый простой вариант. Интрига в том, что оптимальная маркетная ТС должна меняться/подстраиваться с обработкой каждого следующего бара — а это очень и очень непросто.

В конце этапа 1 мы понимаем, что на малых таймфреймах оптимальная ТС работает в минус (комиссия и проскальзывание убивает доход от сделки), а на больших — дает жалкие 30% годовых при DD 10% от депо.

2. Построение оптимальной лимитной ТС

Лимитная ТС — это торговая система, работающая путем выставления лимитных ордеров (потенциально убираем комиссию и проскальзывание). Соответственно, в ход идет обработка всего массива OHLC. Вычисления становятся значительно сложнее. Так же, как в п. 1, речь идет о нестационарной системе — она подстраивается на каждом баре.

( Читать дальше )

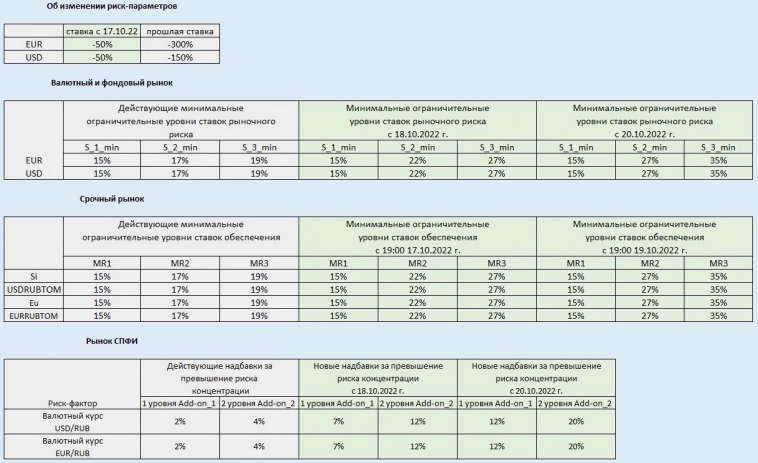
(консолидированная «копипаста» с сайта НКЦ)

НКЦ выполняет функции клиринговой организации и центрального контрагента на рынке ценных бумаг в целях обеспечения поддержания стабильности на обслуживаемом рынке, снижения транзакционных издержек (неттинг) и кредитного риска контрагента.

Система риск-менеджмента:

Для поддержания требуемого уровня надежности НКЦ введена система риск-менеджмента, состоящая в том числе из:

• критериев допуска участников клиринга
• уровней защиты ЦК
• процедур дефолт-менеджмента

Данная система позволяет НКЦ выполнять свои обязательства перед добросовестными участниками клиринга в случае дефолта одного или нескольких участников.

( Читать дальше )

Коллеги!
Есть два варианта как получать данные в квике в рамках луа-скриптов.
1. getCandlesByIndex
2. CreateDataSource

Первый вариант неудобен тем, что нужно держать открытыми графики и, если используются разные тф, то нужно держать больше открытых графиков. Всё это неудобно, когда меняются контракты и тд. Зато надёжно. Если ты графики создал, то источники создались и скрипты отработают.

Второй вариант неудобен тем, что не всегда источники данных создаются, нужно выжидать тайм-ауты и всякое такое.

Подскажите, какой из вариантов вы считаете наиболее правильным/оптимальным или какой используете сами?
Если накидаете пример кода как это используете, буду премного благодарен!

Тетта опциона (теоретическая скорость распада с течением времени) — это не просто «доход» для тейдера, занимающего короткую позицию.

Это компенсация риска потерь, с которым сталкивается инвестор в результате отрицательно асимметричной экспозиции к изменению базового актива.

Тетта-банда (https://www.reddit.com/r/thetagang/ ) и опционные гуру — шарлатаны хотят заставить вас поверить, что тетта — это форма альфы, или бесплатные деньги для истинно верующих.

Опционы — это выпуклые инструменты с асимметричной профилем выплат — покупатели могут заработать намного больше, чем они рискуют потерять, и наоборот для продавца.

Когда вы занимаете отрицательно асимметричную позицию, любое крупное движение приводит к убытку. Если базовый актив движется в благоприятном направлении, вы выигрываете от этого все меньше и меньше; если он движется против вас, вы теряете все больше и больше, поэтому мы можем записать стоимость опциона как:

V(x, t, v)

где x — цена базового актива, t — время, v — подразумеваемая волатильность, а V(.) — стандартный метод определения цены опциона (например, Блэк-Шоулз или биномиальное/триномиальное дерево)

( Читать дальше )

Доброй ночи, коллеги!

Рыночные исследования продолжаются. После 4-х задач мы придем (если доживем) к формулировке принципа неопределенности Гейзенберга для рыночных цен.

Первая задача здесь: smart-lab.ru/blog/834656.php

Усложним ее условия.
Точную цену (154) мы знаем не через год, а примерно.
Ну т.е. в неопределенный нормально распределенный момент времени со средним 1 год и дисперсией d2.
Годичная дисперсия самого ценового процесса равна d.

ВОПРОС:
Какой максимальный доход на капитал в $1000 мы можем получить при этих вводных?

P.S. Ранняя публикация связана с анонсом, что задачка № 2 давно решена

Доброй ночи, коллеги!

Рыночные исследования продолжаются. После 4-х задач мы придем (если доживем) к формулировке принципа неопределенности Гейзенберга для рыночных цен.

Первая задача здесь: smart-lab.ru/blog/834656.php

Усложним ее условия.
Через год мы знаем не точную цену, но цену, нормально распределенную вокруг цели (154) с дисперсией d1.
Годичная дисперсия самого ценового процесса равна d.

ВОПРОС:
Какой максимальный доход на капитал в $1000 мы можем получить при этих вводных?

P.S. Особо отмечаю, что правильный ответ к задаче № 1 озвучил только Eugene Logunov. Точного доказательства он не предъявил, но привел ссылку, по которой любой желающий может попробовать его восстановить. Жаль, предфинальную идею высказали не менее 5 чел., но никто из них не смог довести свои рассуждения до конца.

Доброй ночи, коллеги!

Речь, собссно, про smart-lab.ru/blog/834656.php

Обсуждение получилось креативным, многие вплотную подошли к решению, но все же не дошли...

Попробую дать наводящие соображения (давать ответ неинтересно).

Сначала разберем случай МО=0

1. Разобьем годичный интервал на N меньших интервалов (баров)
2. На первом баре пох, какое торговое решение принимать — МО результата будет 0
3. На 2-м и т.д. вплоть до предпоследнего та же картина
4. На последнем баре надо торговать на возврат к 154 (ниже — покупаем, выше — продаем)
5. Распределение цены в начале последнего бара известно
6. Осталось взять финрез сделки с максимальным плечом и проинтегрировать его по этому распределению
7. И потом устремить N к бесконечности (вариант — положить N равным числу минут/секунд в году))))

В случае МО<>0 оптимальная стратегия на всех барах (кроме последнего) — B&H (или S&H).
Однако простой подсчет показывает, что результат последнего бара перевешивает предыдущий доход.

( Читать дальше )