парный трейдинг
Парный трейдинг. Кто гуру этого рынка?
- 04 августа 2015, 18:17
- |
- Гринькин Константин проект 1000 процентов, на ЛЧИ 2014 заработал 2 или 3 млн
- Клевцов Антон юнайтед трейдерс, много читает вебинаров по данной теме и на сайте информация что зарабатывает кучу денег с этого вида торгов
- Александр Бутманов проект дрим тим, один из первых начал говорить о парном трейдинге и баскет трейдинге
Колееги кто что знает про них, стоит ли к ним прислушиваться, и реально ли заработать при парном трейинге.
PS если есть еще имина гуру данного вида торговли, пишите с описаниями.
Корреляционный сигнал
- 31 июля 2015, 09:01
- |
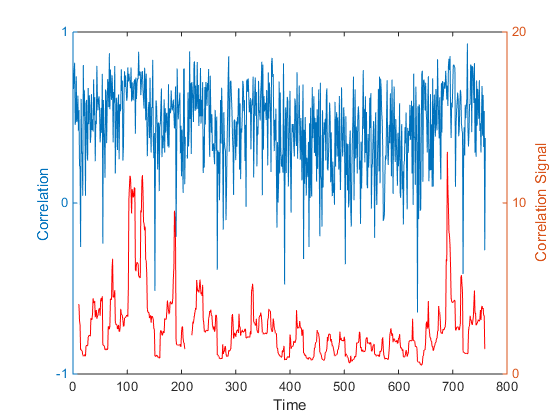
Использование корелляции широко распространено в финансовой теории и практике, от создания портфелей до стратегий статистического арбитража.
Основная сложность в применении корелляции это ее изменчивость: активы, которые в один момент времени кажутся практически некоррелироваными для целей хеджирования, могут стать высококореллироваными в другие моменты времени, например, при высокой активности рынка. Напротив, акции, кажущиеся подходящими для парной торговли, в связи с высокой корелляцией их приращений цены, могут позднее показать разнонаправленную динамику, приводящую к значительным потерям.
Нестабильность уровня еще усугубляется эмпирическими выводами о том, что волатильность корреляции сама по себе зависит от времени: в одно время корреляция между активами может плавно меняться в узком диапазоне, в другое время мы можем наблюдать изменения знака коэффициента корелляции в течении нескольких дней.
( Читать дальше )
Торгуем пару акций Газпром против Роснефти (GAZR/ROSN)
- 29 июля 2015, 15:54
- |
Предлагаю вашему вниманию для разбора одну из самых распространенных пар на российском рынке.
Сегодня мы рассчитаем доходность парного тренинга, где будет торговаться Газпром против Роснефти
Для начало взглянем на графики фьючерсов на данные акции за 12 месяцев:
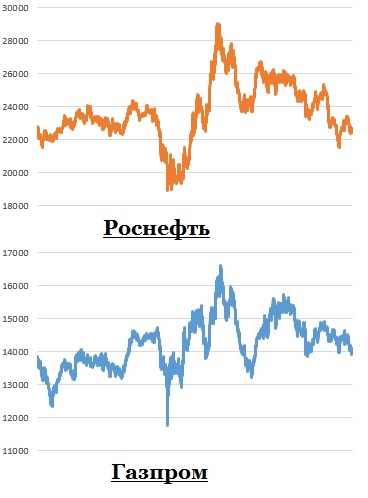
Корреляция заметно даже на глаз, соответственно предлагаю рассчитать пару 2*GAZR — 1*LKOH
( Читать дальше )
Сколько пар можно построить из 11 фьючерсов
- 23 июля 2015, 13:32
- |
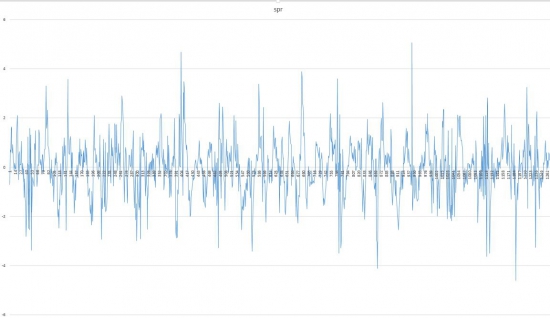
Ответ прост, из 11 наиболее ликвидных фьючерсов (gaz,lkoh,rosn,sngr,gmk,sbrf,sbpr,vtb,si,rts,br) на российском рынке можно построить 55 разных пар.
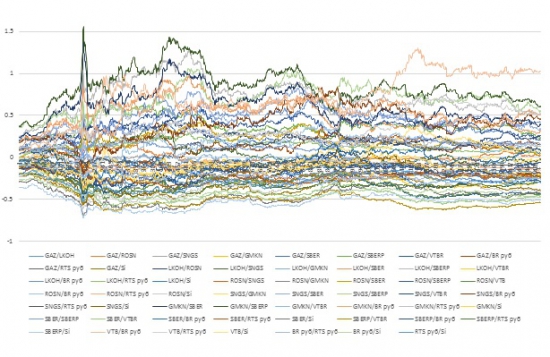
Конечно не все из этих пар будут приносить стабильный доход, но если применить фильтрацию и отобрать лучшие пары по показателям то торговать можно 10-20 разных торговых пар.
А теперь давайте предположим какое кол-во разных стратегий можно построить выбрав 10-20 пар с хорошей доходностью, перебирая такие параметры как шаг котирования, динамическая нулевая линия и шаг выхода, мы можем построить более 500 разных стратегий, сделки по которым пересекаться на будут.
Если кому необходим файл со спредами который был построен на основании 55 пар, вы можете писать в личку.
или самостоятельно можете скачать с сайта http://www.saturn-capital.info/#!about1/c1od
Статистический арбитраж - виды алгоритмов на одной схеме
- 01 июля 2015, 12:27
- |

По мере времени буду выкладывать принципы и тесты данных стратегий.
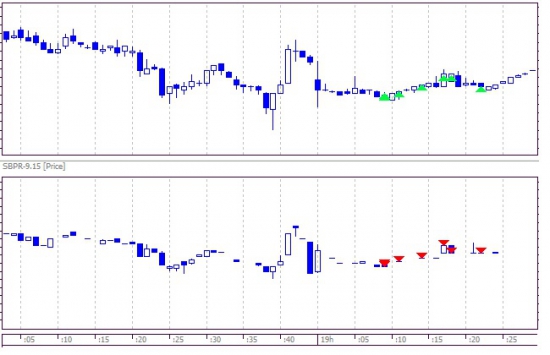
Торгуем подобные спреды:
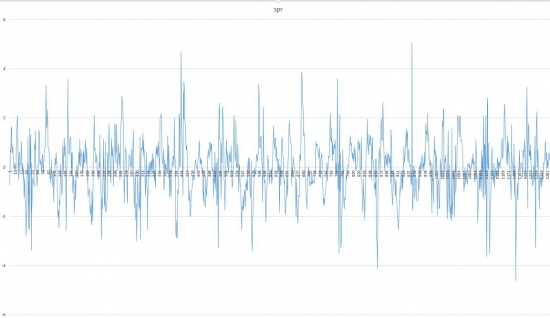
Робот арбитражник на TsLab
- 26 июня 2015, 19:19
- |
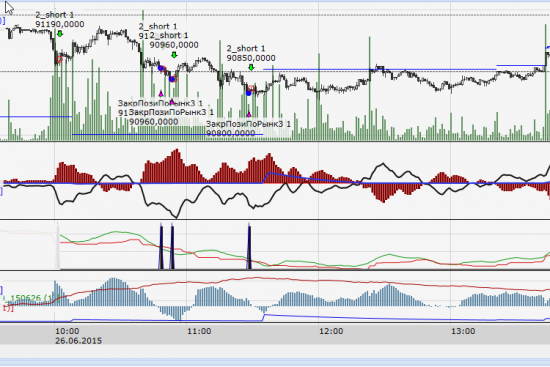
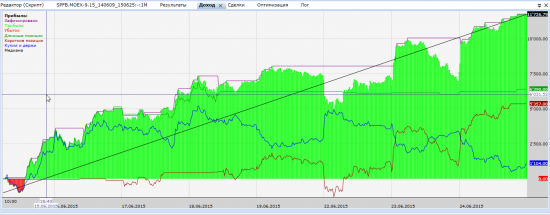
( Читать дальше )
Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
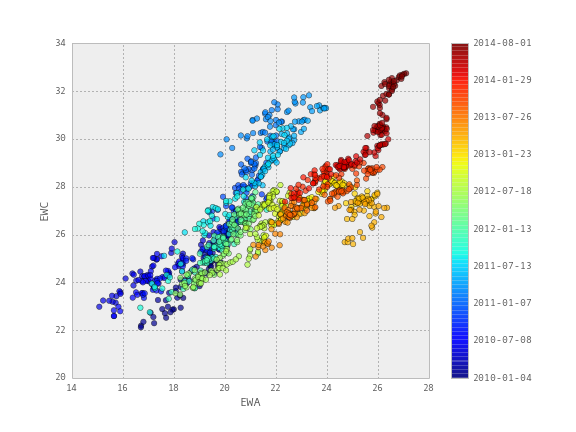
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
Оптимизации стратегии парного трейдинга, превращаем убыточную пару в прибыльную.
- 22 апреля 2015, 14:14
- |
Для примера возьмем стандартную пару GAZR-LKOH, за предыдущие 12 месяев при стандартрыйх настройках пара принесла убыток в 37%, максимальная просадка 50%. (стандартные настройки eMA 500, тру уровня котирования 800, 1600, 2400, выход из позиции у средней)
Итоги торгов пары GAZ-LKOH
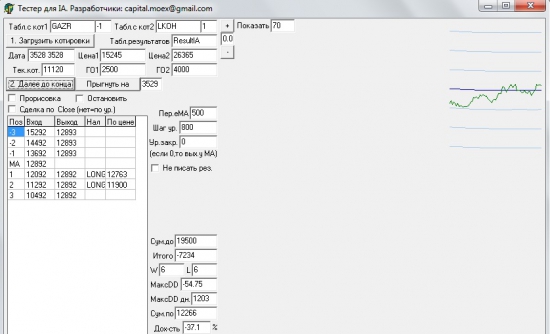
Что мы можем сделать в этом случае для улучшения прибыльности.
Первый вариант изменить коэффиценты весов инструмента А и инструмента Б, давайте сделаем к примеру соотношение 3 GAZ и 1 LKOH
Второе что мы можем изменить это динамический нулевой уровень, предлагаю взять eMA с периодом 600
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал