марковиц
Как составить портфель, чтобы не бояться просадок
- 16 июля 2020, 14:59
- |
Предложенный взгляд будет валидным, если вы на протяжении всего периода инвестирования рассматриваете пропорции портфеля как константу: покупаете ценные бумаги в желаемой пропорции и точно в такой же пропорции по мере необходимости их продаете (тем самым сохраняя пропорцию оставшейся части портфеля). Но разве эта схема будет удачной с точки зрения входа и выхода из ценных бумаг? Ведь логичней продавать те бумаги, которые сейчас стоят максимально дорого, а не все входящие в портфель.
Например, представьте ситуацию, что вы получили крупную сумму денег, как оплату за выполненние длителного проекта. Если для простоты рассмотрения ограничиться только валютными инвестициями, то чтобы максимально выгодно тратить эти деньги на текущие расходы, лучше всего разложить эти деньги в три валюты: рубль, доллар и евро. Это позволит тратить каждый из активов в тот момент, когда он имеет максимальную стоимость относительно двух оставшихся. Например, если сегодня бивалютная корзица стоит дорого, а доллар вырос отностельно евро, то выгоднее продавать доллары, позволяющие сегодня получить максимальную выгоду. Таким образом каждый из активов будет продан по максимуму своих цен. *
( Читать дальше )
- комментировать
- 5.6К | ★5
- Комментарии ( 3 )
Составление инвестиционного портфеля по Марковицу
- 05 января 2020, 16:03
- |
Обобщённый подход к диверсификации рисков
- 28 августа 2019, 04:47
- |
- Обобщённая проблема
Результаты оценки любых случайных величин представляют из себя случайную величину. Не исключением здесь будут оценки ковариации.
Особенно сильно эффект неточности полученных оценок (случайности статистик) будет проявляться в портфелях, составленных из большого количества ценных бумаг — большего или сопоставимого количеству располагаемых наблюдений. И, поскольку, в некотором приближении задача портфельного инвестирования сводится к поиску двух максимально независимых активов из множества:
где R — коэффициент взаимной корреляции — её решение, естественным образом, будет располагаться в области максимально отрицательной статистической ошибки.
( Читать дальше )
Портфельная оптимизация как бустинг на «слабых» моделях-3
- 21 августа 2019, 13:49
- |
Устойчивые долгосрочные модели
В предыдущих частях (часть 1, часть 2) мы рассмотрели построение композитных систем оценок ценных бумаг, построенных при помощи распространённых средств машинного обучения (Bag/Boost методы). Однако, такой подход, несмотря на все свои преимущества (скорость, точность) имеет ряд больших недостатков – отсутствие универсальности моделей в результате проблем «переобучения» (точной настройки на определённые типы рынков и временные интервалы) и сложность интерпретации полученных композиций.
В результате решения этих проблем мы разработали базовую модель на основе наших представлений о стохастических дифференциальных уравнениях с квантовыми скачками, образующих улыбку волатильности. Эта макромодель получила в наших исследованиях наиболее полную микроскопическую интерпретацию.
( Читать дальше )
Консенсус прогноз. Готов для включения в инвестиционный бюллетень
- 23 апреля 2019, 13:14
- |
Друзья!
Добил модуль консенсус прогнозов. И скорее всего он будет включен в следующий инвестиционный бюллетень.
Кроме расчёта самих консенсус прогнозов с учетом вероятности их исполнения (писал в прошлый раз https://smart-lab.ru/blog/534364.php), я добавил часть, в которой смешиваются исторические данные по ожидаемой доходности с консенсус прогнозами с учётом разных степеней доверия для каждого из показателей.
Вот так это выглядит в табличке (описание столбцов описывает суть расчётов)
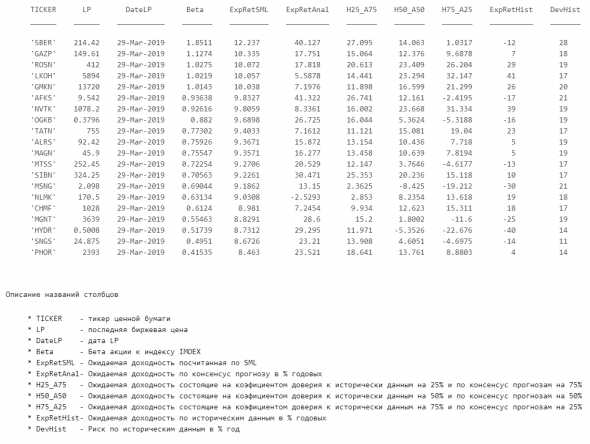
Также я добавил расчёт ожидаемых доходностей по Security Market Line (SML), чтобы было удобнее сравнивать бумаги, которые интереснее взять в портфель, а для каких лучше купить ETF
( Читать дальше )
Портфельная оптимизация как бустинг на «слабых» моделях
- 09 апреля 2019, 23:20
- |
Часть 1.
Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.
Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы) или торговые системы.
Решение задачи состоит из двух этапов:
- Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
- Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.
Почему мы используем аналогию портфельной оптимизации с методами машинного обучения — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации – была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).
( Читать дальше )
«Принципы» Рэя Далио. Конспект. Часть 11. Священный Грааль инвестирования. Моя «неразрешимая» проблема
- 04 января 2019, 12:10
- |
Священный Грааль инвестирования

Правильная диверсификация — залог снижения рисков без снижения доходности. Если бы мне удалось сформировать инвестиционный портфель из высококачественных потоков доходности*, который был бы правильно диверсифицирован (прямые на графиках уравновешивают друг друга), мои клиенты получали бы более устойчивую и надежную совокупную доходность портфеля, чем в любом другом месте.
Лауреат Нобелевской премии по экономике Гарри Марковиц** разработал модель, ставшую впоследствии очень популярной, которая позволяла вводить данные по набору активов вместе с их ожидаемой доходностью, рисками и корреляциями (отражающими, как эти активы показывали себя в прошлом) и определять «оптимальное соотношение» этих активов в портфеле. К сожалению, эта модель ничего не говорила об увеличивающемся эффекте от изменения любой из указанных переменных или о том, как действовать в случае неуверенности в каком-то из предположений.
( Читать дальше )
Оптимизация портфеля акций
- 30 декабря 2018, 16:40
- |
Здравствуйте друзья. Изучая вопрос портфельного инвестирования для долгосрочной перспективы наткнулся на работы Гарри Марковица. Изложенные им труды показались достаточно логичными и легкореализуемыми в условиях сегодняшней компьютеризации. Основные идеи Г. Марковица, которые были использованы для составления портфельной модели:
- Величина риска – стандартное квадратическое отклонение доходности за расчетный период
- Уровень риска портфеля – умножение ковариационной матрицы на два вектора частей акций, входящих в портфель
Перед тем как начать, дам определение некоторым понятиям, использованным в статье:
- Портфельная модель – ряд ограничений, накладываемых на параметры (доходность, риск и т.п.) акций перед добавлением их в портфель.
Целью данной работы являлось создание портфельной модели, критерием оценки которой является доходность.
Портфельная модель разрабатывается для отечественного фондового рынка. Торговые инструменты (акции) входящие в расчет взяты из индексов MICEX (Oil & Gas Indices; Consumer Goods & Retail Indices; Chemicals Indices; Metals & Mining Indices; Telecoms Indices; Electric Utilities Indices; Financials Index; Transport Index), в количестве 76 единиц. Расчетный период – один месяц.
( Читать дальше )
Софт для оптимизации портфеля по Марковицу
- 26 декабря 2017, 02:35
- |
Решил заняться рассчетами портфелей по Марковицу. Для начала посмотрел вебинар «Создание инвестиционного портфеля» от авторов сайта «Рост сбережений», в котором пошагово разъясняются все рассчеты в Excel.
В итоге сделал вывод, что рассчитывать портфели в Excel вполне реально, но долго. Дело в том, что довольно много повторяющихся операций нужно выполнять вручную, а значит возможны ошибки. Да и странно это — изобретать велосипед, ведь задача эта довольно стандартная и ее можно автоматизировать.
Далее я выяснил, что в таких программах, как R и Matlab, рассчеты можно выполнять быстрее, да и подгрузку данных можно автоматизировать.
Для R и Matlab созданы пакеты для финансового анализа и есть много готового кода, в котором параметры можно менять под себя.
На первый взгляд графический интерфейс Excel удобнее и знаком многим, но адаптировать несколько строк кода под себя тоже не слишком трудно.
Кто-нибудь на Смартлабе имеет опыт рассчета портфелей в этих программах? Что лучше выбрать? (R бесплатна, а Matlab тоже можно получить бесплатно, так что вопрос цены не рассматриваем). Может есть другие программы для этого? Можно ли рассчитывать оптимальные портфели в Wealth-Lab, amibroker и аналогах?
Бенджамин Грэхем. Гарри Марковиц. один нюанс
- 27 сентября 2017, 14:17
- |
Уважаемый Александр Здрогов как всегда написал интересно:
smart-lab.ru/blog/422872.php
Как Вы знаете, Грэхем и Марковиц-это реальные, невыдуманные авторитеты. Думаю, тут все согласны.
А теперь два вопроса:
Почему Бенджамин Грэхем не инвестировал «По Деревне Грэхема и Додда»?
Почему Гарри Марковиц инвестировал 50/50, а не «по Марковицу»?
Имхо, это важнейшая точка в Трейдинге, Инвестициях, называйте как хотите...
Спасибо
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
