Избранное трейдера WooDoo
Опционы: Урок№1. Сходство опционов с другими инструментами
- 26 сентября 2022, 14:08
- |
В этом уроке разбираю сходство опционов с другими биржевыми инструментами. Показываю в торговых терминалах Interactive Brokers и Deribit как открывать позиции на опционах, отправлять заявки, совершать сделки.
Видео будет полезно для желающих разобраться в опционах с нуля. Для тех, кто хочет начать торговать на американском рынке опционов или на криптовалютном рынке: биткоин, эфир, солано.
( Читать дальше )
- комментировать
- 3К | ★16
- Комментарии ( 21 )
Оценка бессрочных облигаций, и как это может помочь при оценке вечного фьючерса на USDRUB
- 14 июня 2022, 10:22
- |
Обратил внимание, что многие не знают, как правильно оценить вечную облигацию. Однако, ее оценка существенно проще, чем оценка обычных облигаций. Давайте разберемся, как можно оценить бессрочную облигацию.
Как мы знаем внутреннюю (приведенную стоимость) облигации можно оценить с помощью следующей формулы потока платежей: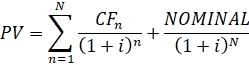
Где:
CFn – купоны
NOMINAL – сумма, которую получит инвестор при погашении облигации
i – ставка доходности
n – год получения купона
N – последний год
PV – приведенная стоимость облигации
В бессрочной облигации нет погашения номинала – NOMINAL, и количество платежей бесконечно, тогда формула принимает вид:
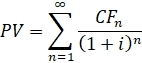
( Читать дальше )
Бесплатный вебинар: Разработка торговых роботов на языке С#. 5 апреля в 19:00
- 31 марта 2022, 14:13
- |

Всех, кому интересен алготрейдинг и программирование, мы приглашаем на бесплатный вебинар «Программирование торговых роботов на С#», который пройдет 5 апреля в 19:00 на нашем YouTube-канале https://www.youtube.com/c/LIVEInvestingGroup/featured
Программа вебинара:
1. На чем пишут роботов?
2. Преимущества С#
3. Фреймворки для алготрейдинга
4. Коннекторы к биржам
5. Разработка, тестирование и оптимизация роботов
6. Как выйти на новый уровень алготрейдинга
( Читать дальше )
FAQ по платежной системе UnionPay и Телеграм канал по этой системе. В избранное.
- 12 марта 2022, 21:44
- |
1. Что это вообще такое?
UnionPay (UP, «Юпи», читается «Юнион Пэй») — китайская карточная платежная система, аналог и конкурент Visa и MasterCard, но при этом не Visa, не MasterCard, не JCB, не МИР и не American Express. Третья платёжная система в мире по известности после «двух гигантов».
2. Где она популярна?
Утверждают, что «в 180 странах мира», в основном, конечно, в Китае и странах Юго-Восточной Азии (Таиланд, Сингапур, Малайзия, итд). Весьма популярна в ОАЭ и странах Персидского залива, в Турции и даже в СНГ (Узбекистан, Таджикистан).
3. Зачем оно мне?
Кратко — чтобы иметь возможность платить за рубежом, как на сайтах, так и в магазинах и кафе, снимать деньги в банкоматах за границей, т.е. пользоваться картой и дальше.
Почему так — да потому что карты российских банков больше не работают за рубежом. Вы не сможете оплатить что-то на зарубежных сайтах российскими картами Visa и MasterCard за несколькими исключениями типа AliExpress, который научился принимать «МИР». Не сможете не только оплатить в магазине, гостинице, в кафе или снять деньги в банкомате, но и оплатить что-то на иностранном сайте в интернете, где нужно вводить данные своей карты.
( Читать дальше )
- комментировать
- 16.8К |
- Комментарии ( 40 )
Графики спроса и предложения в QUIK
- 31 января 2022, 13:30
- |
Для этого тебе нужно построить графики спроса и предложения в QUIK. Повторяй за мной:
Зайди в Quik. Открой график. Нажми на графике правую кнопку мыши. В открывшемся меню жми пункт Добавить график (индикатор) — откроется окноДобавить график. В нем следуй по красным стрелкам:
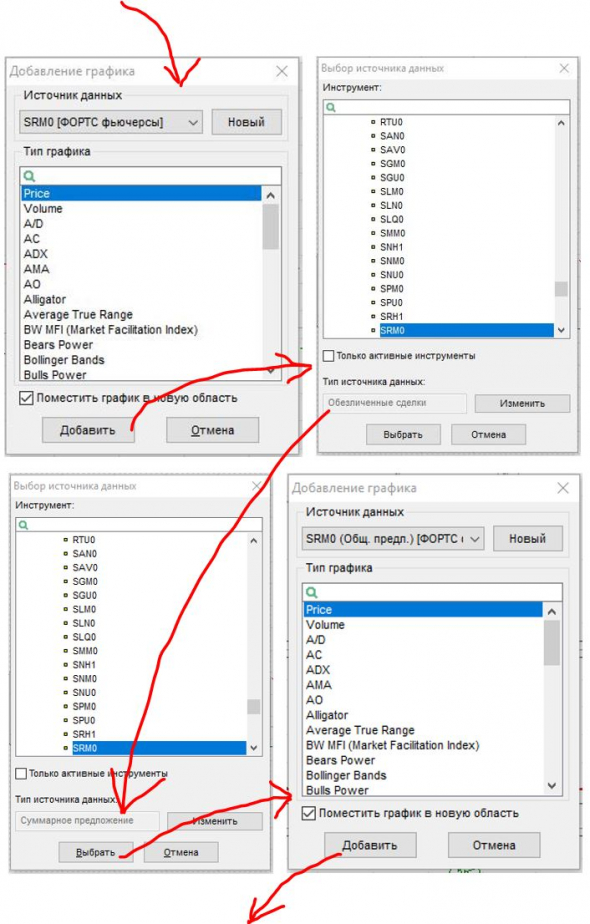
Так ты получишь график Суммарного предложения под графиком цены. После этого повтори процедуру (для Суммарного спроса).
В результате у тебя получится такой дополнительный красивый график, показывающий динамику Спроса и Предложения:
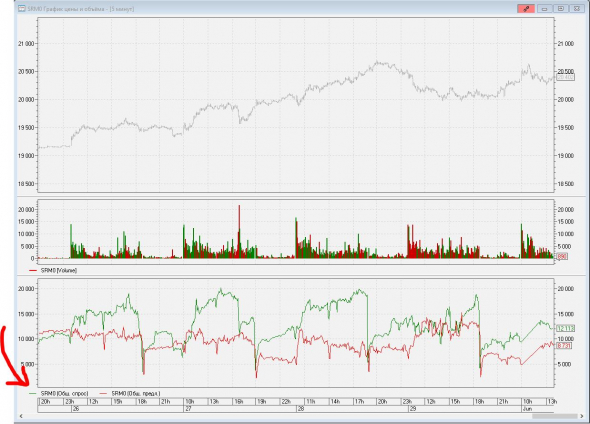
( Читать дальше )
Опционный конструктор
- 30 декабря 2021, 23:46
- |
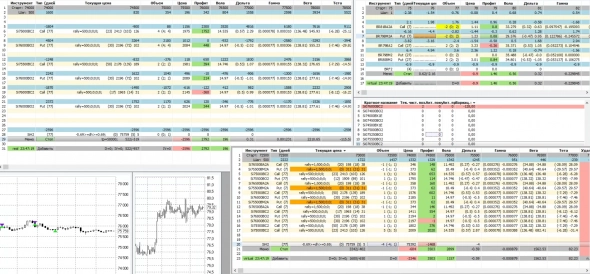
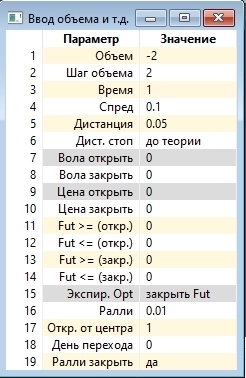
( Читать дальше )
Историческая волатильность "по-быстрому" для TradingView
- 24 ноября 2021, 10:00
- |
// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
//@version=4
study("Historical Volatility")
// Настройки окон
HVPeriod1 = input(17, minval=1, title="Окно 1")
HVPeriod2 = input(34, minval=1, title="Окно 2")
HVPeriod3 = input(51, minval=1, title="Окно 3")
HVPeriod4 = input(85, minval=1, title="Окно 4")
// Настройка периода для сглаживания
EMAPeriod = input(17, minval=2, title="Период сглаживания")
// Собственно индикатор
// мультипликатор, для нормирования к году
mul = 252 * 1210 / timeframe.multiplier
//приращение за бар
ch = log(close) - log(close[1])
// Историческая волатильность в окнах
HV1 = ema(sqrt(sum(ch * ch, HVPeriod1) * mul / HVPeriod1) * 100, EMAPeriod)
HV2 = ema(sqrt(sum(ch * ch, HVPeriod2) * mul / HVPeriod2) * 100, EMAPeriod)
HV3 = ema(sqrt(sum(ch * ch, HVPeriod3) * mul / HVPeriod3) * 100, EMAPeriod)
HV4 = ema(sqrt(sum(ch * ch, HVPeriod4) * mul / HVPeriod4) * 100, EMAPeriod)
// Рисуем красивое
plot(HV1, color=#cccccc)
plot(HV2, color=#ffcccc)
plot(HV3, color=#ff9999)
plot(HV4, color=#ff0000)
Чтобы использовать, копируем, в TradingView открываем Редактор Pine, создаем там новый индикатор (Открыть -> Новый индикатор), удаляем все что там в скрипте по умолчанию и вставляем этот код. Жмем Сохранить. Дальше скрипт будет доступен в выпадающем списке над графиком под кнопкой Индикаторы во вкладке Мои скрипты. Модно, быстро и удобно )Держим опционный строй даже когда на море качка!
Коннектор к Quik через Wealth Lab 7.0
- 19 ноября 2021, 16:33
- |
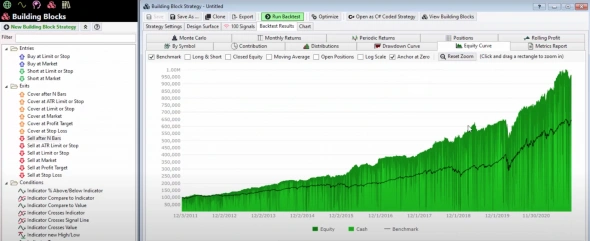
Друзья, насколько вы все знаете, для back test существовала отличная программа для алготорговли WealthLab 6.
Я пользовался ей ещё 8-10 лет назад. Она поражала своей простотой и удобством. Её использовали все алго тестеры в «кулуарах».
К сожалению нормальной адаптации между Quik и Wealth Lab никогда не было. Либо она очень плохо поддерживалась, либо чего — то не хватало и т.д. Также на тот момент Quik выдавал данные только через DDE.
Поэтому, я, как и многие другие, тестировал бота в WLD, а потом шёл переписывать его на какой — то другой платформе. На тот момент я писал на S#. Переписка обычных timeFrame стратегий на S# не очень благородное дело, потому что S# — это библиотека больше для реализации сложных ботов, ибо 30% кодинга это алгоритм, а 70% — это создания самого .NET проекта. (windows exe приложения) S# больше подходит для реализации нестандартных ботов.
Прошло время и много моментов поменялось.
Во-первых, вышла новая версия WLD 7.0 и её можно оплачивать ежемесячно, она стоит всего 40$ в месяц.
( Читать дальше )
TesterDashboard - эффективное привлечение эволюционной интеллектуальной машины к поиску закономерностей.
- 14 октября 2021, 02:30
- |
Идея не нова, вопрос был только в реализации.
Платформа MetaTrader 5 обладает возможностями автоматизации Тестера. Расчет огромного количества данных на истории реальных тиков — обыденность.
Проверка адаптивности ТС — аналогично.
Обработка расчетов.
Однако, при большом количестве уже проведенных вычислений требуется разобрать эту кучу данных и найти в ней что-то, действительно, интересное.
Это можно делать двумя способами:
- Создать автоматический критерий, который отфильтрует что-то стОящее от вычислительной шелухи.
- Перебрать руками каждый кусочек цифровой кучи, доверяя фильтрацию мощной интеллектуальной машине — головному мозгу человека.
В первом случае получается быстро, но можно легко что-то упустить, действительно, важное.
Во втором случае все гораздо тщательнее, но очень много времени на это уходит. Элементарно утомить природную машину настолько, что больше никогда не захочется к этому возвращаться.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал


