SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
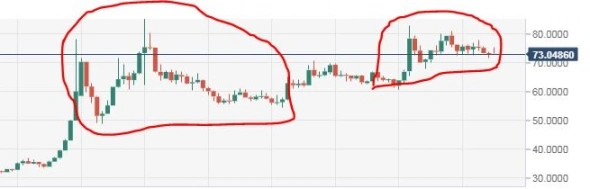
фракталы
РТС: опасно
- 26 апреля 2021, 08:04
- |
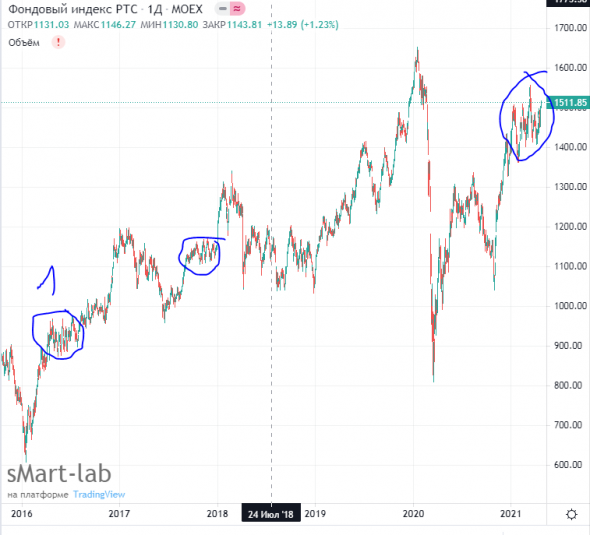
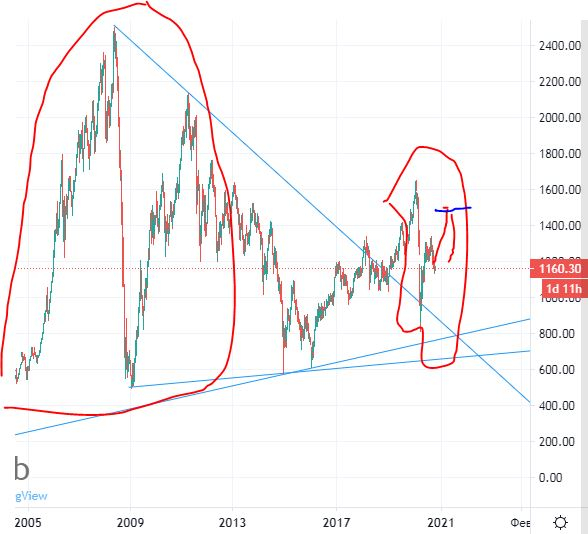
Ничего нового наверное не будет в кружке 1 апрельская ситуация отторговали что-то подобное
волосатое с набором позиции и пошли выше
если ничего нового в финансах не происходит, то «наверное пойдет выше 1600
2048 давно за эту цель
День числа Пи
- 14 марта 2021, 15:25
- |
Поздравляю всех с Международным Днём числа Пи!

( Читать дальше )

В незапамятные участвовал в конкурсах работ МАН. Сам по математике, но однажды оказался зрителем на докладе в секции биологии. Работа была посвящена изумительному наблюдению, подкрепленному большим числом замеров: окружность любого муравейника примерно втрое длиннее его диаметра. © Константин Иванов

( Читать дальше )
Чего жду от Доллара
- 03 декабря 2020, 09:15
- |
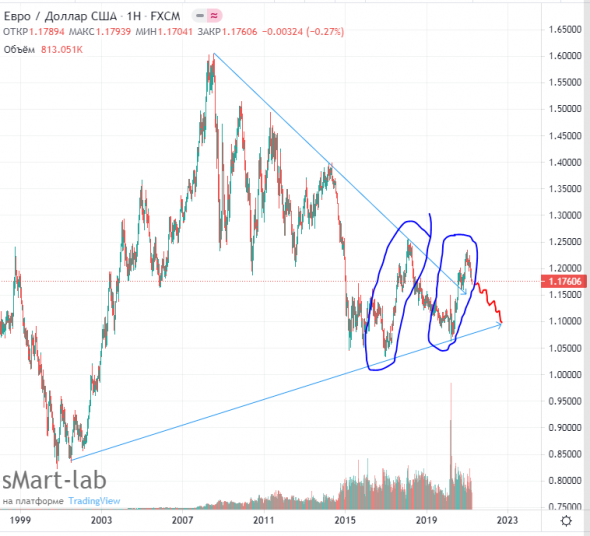
Доллар ничего нового не придумал
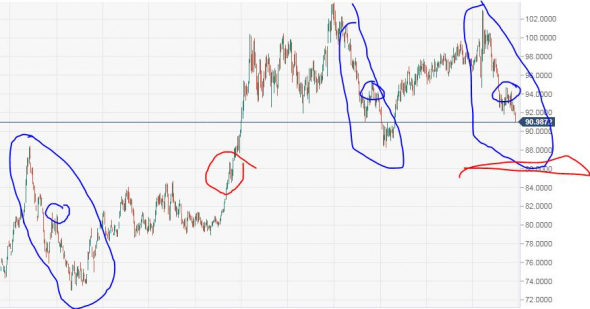
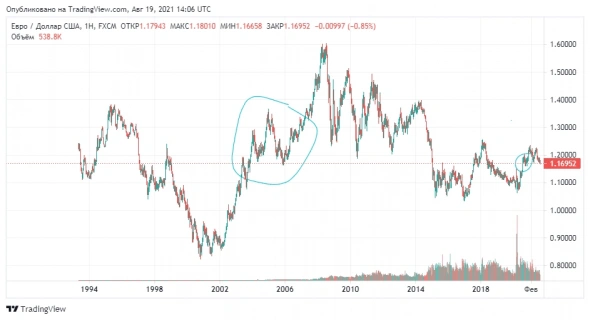
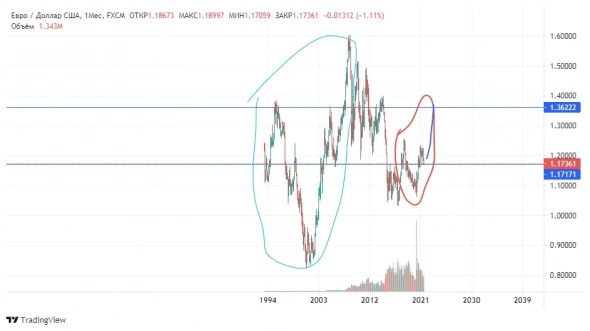
наверное пока что не самое удачное время для доллара, а диапазон разворота либо кратковременного от-скока это евро 1.33-1.36
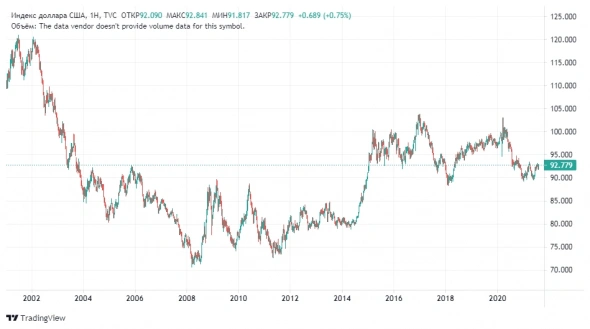
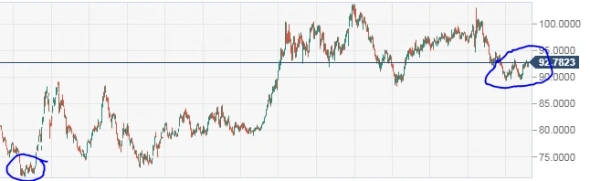
смотри мои прежние посты=я предполагал, то и вышло-ниже 92 и не надо быть с высшим образованием магистром финансов, что бы этого не увидеть

наверное пока что не самое удачное время для доллара, а диапазон разворота либо кратковременного от-скока это евро 1.33-1.36
смотри мои прежние посты=я предполагал, то и вышло-ниже 92 и не надо быть с высшим образованием магистром финансов, что бы этого не увидеть
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал