акции сша

Начну с текущих экспираций.
Пятница — хлебный день для многих опционщиков на рынке США.



А вы говорите, нет ликвидности в стакане (РФ), а тут такое каждую пятницу.
Я денег пригнал маленько на IB (6000 usd), буду отстреливать коллами/путами лебедей, на следующей неделе.

А сегодня, у нас дайджест комментарии сбывшихся, а может и не сбывшихся прогнозов. В прошлый раз нормально совпало: smart-lab.ru/blog/532105.php

* ОБЩИЙ МИРОВОЙ ПРОФИЛЬ:
   базовые композиции, так называемый АЛЛЮР. 



( Читать дальше )

В своей книге «Эпоха инвестора» Уильям Бернштейн описывает мифического работодателя по имени Дядя Фред, который предлагает инвесторам схему пенсионных накоплений, определяемых броском монеты. Одна сторона монеты дает + 30% годовой прибыли, в то время как другая сторона дает вам -10% потерь в данном году.

Поскольку бросок монеты дает вам шанс 50/50 на каждый результат, это даст инвесторам совокупный годовой доход в размере около 8,2% со стандартным отклонением 20%, что не слишком далеко от фактических долгосрочных результатов на фондовом рынке.

Допустим, вы решили вносить 1000 долларов в год в течение следующих 40 лет в программу дяди Фреда. И давайте далее предположим, что бросок монеты сработает, чтобы дать вам 20 positive return лет подряд, а затем 20 negative return лет подряд. В этом случае вы получите чуть более 100 000 долларов. Неплохо, но вы едва поспеваете за показателями долгосрочной инфляции.

Мы также можем взглянуть на противоположную сторону этой монеты — 20 лет подряд отрицательной доходности, а затем 20 лет подряд положительной доходности. На этот раз ваше вложение вырастет до более чем 2,3 миллиона долларов!

( Читать дальше )

Главные темы Солодин LIVE:

— Самые перспективные направления в биотехнологиях в 2019 году.

02:09 — Иммунотерапия рака. CAR-T технологии.
06:05 — Слияния и поглощения в секторе биотехнологий США.
14:10 — Цифровая терапия (Digital Therapeutics)

— В какие Biotech ETF лучше инвестировать деньги в 2019 году?

15:43 — IBB (iShares Trust NASDAQ Biotechnology ETF)
16:38 — XBI (SPDR S&P BIOTECH ETF)
17:55 — BIB (ProShares Ultra NASDAQ BIOTECHNOLOGY)
18:25 — Сравнительный анализ этих ETF с индексом S&P500
21:09 — Fidelity Select Biotechnology. Основные характеристики фонда и его состав.

( Читать дальше )

Часть 1.

Традиционно считается, что задача портфельной оптимизации, или задача Марковица, представляет собой некоторую самостоятельную задачу выбора такого портфеля активов, который обладал бы максимальной доходностью при минимальных рисках.

Прим. В качестве актива могут выступать ценные бумаги (акции), их производные (опционы)  или торговые системы.

 

Решение задачи состоит из двух этапов:

1. Прогноз доходности и ковариации активов в будущих периодах – то есть построение некоторого набора «слабых» прогностических моделей.
2. Составление оптимального портфеля в соответствии с некоторой целевой функцией, и ранее полученными оценками. То есть построение такой композиции «слабых» моделей, которая обладала бы наибольшей прогностической силой.

 

Почему мы используем аналогию портфельной оптимизации с методами машинного обучения  — Bag, Boost?! Потому что в действительности (и мы это продемонстрируем) нам абсолютно не важно, насколько хорошо динамику наших временных рядов прогнозируют «слабые» модели – нам важно только то, чтобы ошибки прогнозов наших моделей взаимно компенсировали бы друг друга в некотором интегральном смысле. Иными словами – в случае бустинга – ошибка прогноза линейной композиции была бы минимальной, а в случае портфельной оптимизации –  была бы минимальной ошибка прогноза нелинейной композиции (то есть самого портфеля).

( Читать дальше )

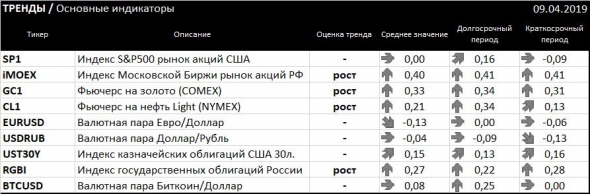
Комментарий:

• Акции США — вероятен разворот вниз от текущих уровней при отсутствии deep buyers в окончании торгов, а они вряд ли будут так как завтра день насыщенный на события.
• Акции РФ все еще подгоняются импульсом исторического максимума и закрытием «санкционных» стоп-лоссов и шортов. Вряд ли этот рост может продлится долго в отсутствии позитива на мировых рынках.
• Золото — рост от текущих уровней может оказаться весьма сильным импульсом к локальным максимумам на 1400.
• Нефть — все еще в растущем тренде, но краткосрочно возможен разворот, опасные уровни для покупки особенно после размещения саудитов, вероятно большие объемы были  захеджированы покупателями через нефтяные фьючерсы.
• Казначейские облигации США (Трежерис) — готовятся к новому росту.
• Облигации РФ (ОФЗ) — возможен новый поход на локальный максимум в отсутствии политических шоков.
• Валюты в неопределенности, но Евро к Доллару выглядит слабее.

t.me/singpoint

Послушав семинар Сергея Григоряна https://www.youtube.com/watch?v=TjOlc2u8TPs&t=2s , решил покопаться в этой теме (Dual momentum)
Через статью в сикиньальфа https://seekingalpha.com/article/4233923-dual-momentum-january-update вышел на сайт https://www.scottsinvestments.com/dual-etf-momentum/ где даны текущие сигналы https://docs.google.com/spreadsheets/d/1S5YVvjIXexBOjonrpgSM0ngr3O-82NGalGnfbj5hOxU/edit#gid=1298415711

Добрый день, друзья
На рынке скоро начнутся новые сильные движения, поэтому я возобновляю публикацию оценок трендов в основных индикаторах и финансовых инструментах. Постараюсь выйти на регулярную основу (при наличии времени на оформление публикаций). На всякий случай рекомендую добавить канал в телеграмме так как там скорость и объем появления информации будет несколько выше.




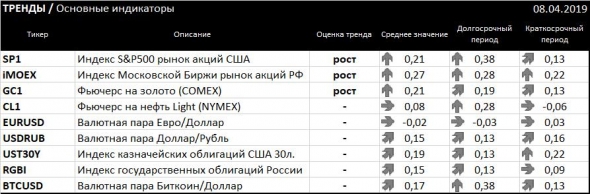
Комментарий: 
Акции США, РФ и нефть все еще в растущем тренде, но возможен разворот с текущих уровней при начале коррекции снижении ниже предыдущих сессионных минимумов. Золото возобновляет рост после коррекции. Евро к доллару нейтрален видимо до новых заявлений ЕЦБ и выхода из узкого диапазона торгов прошлой недели. Доллар к рублю в слабом растущем тренде, ситуация может измениться в любую сторону так как текущие уровни могут быть началом сильной тенденции как в одну так и в другую сторону. Облигации США близки к возобновлению растущего тренда (снижения ставок). Облигации РФ пытаются возобновить рост и вернуться в растущий тренд. Биткоин близок к возобновлению роста при закреплении выше локальных максимумов прошлой недели, но при неудачной попытке вероятно коррекционное движение вниз.

Все больше и больше убеждаюсь на сколько важна диверсификация. Например есть у меня в портфеле WBA -Walgreens Boots Alliance — сеть аптек. Вроде по всем показателям замечательная компания, и растущие дивиденды и растущие прибыля. Были. И тут вышел плохой отчет и акции упали с 63 до 55. И только благодаря тому что доля в портфеле их не большая, портфель за это время не упал а вырос.Такая же история была с UNIT — владелец сотовых вышек и кабелей, который сдает их в аренду другим компаниям. Основной их арендатор оказался на стадии банкротства и UNIT сильно упал.Да и с более серьезными компаниями многое что может случиться, например Боинг сильно просел после падения их самолета, но я их покупал давно и сейчас еще в плюсе.Иногда даже возникают мысли, чтобы только етфы покупать. Сейчас если бы только начинал с небольшой суммы, то покупал бы только етфы.

Сегодня наткнулся (и подписался) еще на одного автора в сикиньальфа https://seekingalpha.com/author/lance-brofman#regular_articles  .
Освещает ETN с левереджем. Например с помощью ETN от UBS - https://etracs.ubs.com/product/list  можно построить хорошо диверсифицированный портфель с двойным левериджем.