Избранное трейдера java
"... там с кодами клиентов инфу транслируют..." ... заинтриговало...
- 25 апреля 2015, 21:35
- |
Заинтересовало обсуждение на сайте Московской биржи:
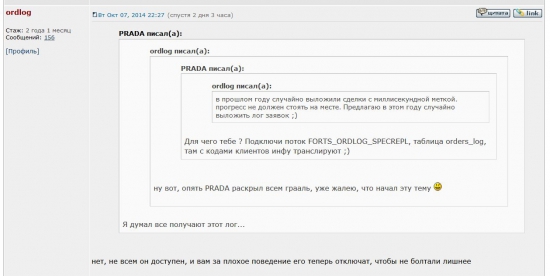
Может кто-то сможет прояснить ситуацию?
Звучит все очень интригующе… насколько понятно из переписки, за отдельную денежку и по другим основаниям некоторые участники рынка получают возможность видеть поток сделок с указанием идентификатора участника… в современных условиях это означает, что такие участники могут вести он-лайн базу позиций участников и использовать ее в своих целях, получая нерыночное преимущество… понятно, что для [очень] крупных участников в этом есть особая прелесть — можно моментально наблюдать сколько участников встало в ту или иную сторону, по статистике предыдущих дней можно прикинуть и размер депо и насколько оно использовано для каждого обезличенного участника и группировать их по категориям, планировать движения против определенной категории и понимать ее массовость/ресурс, просчитывать риски контрагентов, видеть сколько нороду уязвимо с т.з. рисков или их еще нужно завлекать и т.д…
( Читать дальше )
- комментировать
- 73 | ★21
- Комментарии ( 36 )
Торговые роботы. Как распределить капитал между стратегиями
- 25 апреля 2015, 12:01
- |
На почту часто поступают вопросы по поводу распределения капитала между стратегиями. Как добиться стабильных и устойчивых результатов на продолжительном временном интервале? Как эффективно объединить разные торговые роботы в единую систему?
Ниже будет описан собственный подход к данному вопросу. На абсолютную истину он не претендует, но подход вполне логичен, достаточно прост и проверен на собственном опыте. Надеюсь для кого-то это будет полезно.
Затрагивать тонкости построения и оценку качества работы отдельных стратегий не будем. Допустим, в арсенале уже есть несколько торговых стратегий (например 3), основанных на надежных идеях и приносящих вам уже какой-никакой профит. Системы полностью формализованы, оттестированы на исторических данных, имеют достаточный период реальной торговли. Это позволяет уже иметь какие-то ожидания в плане будущего поведения данных торговых стратегий.
( Читать дальше )
Альтернативный расчет стоимости опционов 2. Формула сферического опциона в вакууме
- 24 апреля 2015, 12:06
- |
В прошлых статьях (smart-lab.ru/blog/248456.php, smart-lab.ru/blog/250544.php ). Я пытался написать альтернативную формулу для расчета цен опционов. Но взятая из существующего научного арсенала формула, для проверки гипотезы оказалась не совсем корректна, и даже после подгонки как-то не внушала доверия. Поэтому пришлось делать всё самому с самого начала и придумать свою теорию «распространения взаимодействия», на основе которой и рассчитывать цены опционов.
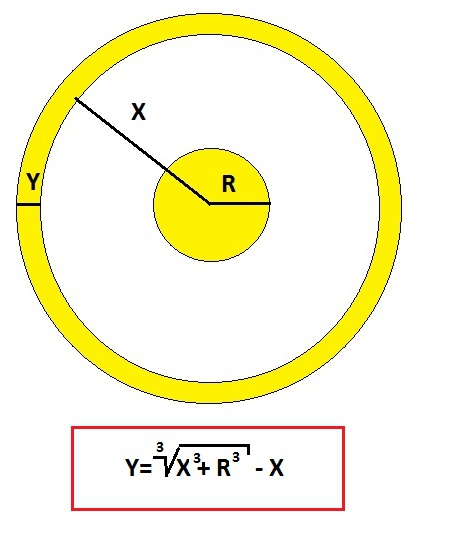
И так, возьмем, к примеру гравитацию (потому как, никто не знает что это такое, а следовательно придирок к мелочам будет меньше). Пусть у нас есть некая точка, оказывающая на окружающий мир гравитационное воздействие. Представим это воздействие а виде шара радиусом R, где сила воздействия равна R. ( для опционов это W – цена опциона на деньгах):
Теперь представим, что шар начинает расширятся, с образованием в центре пустоты, и превращается в некую сферу. Общая сила воздействия (энергия заключенная в R ) остается постоянной. И объем начального шара равен объему оболочки сферы толщиной
( Читать дальше )
Мыслим опционно.
- 24 апреля 2015, 11:08
- |
Отчет совершит закономерные действия с премиями на опционы: до отчета они будут расти, а потом разом упадут. Это поле для работы. Опционы имеют самые разные условия, и этот фактор меняет структуру опционных премий с разными условиями и меняет соотношение риска. Возможность контролировать риск, направлять его, использовать его в своих корыстных целях — это вековая мечта труженика фондовых полей, пахарей денежных нив и возделывателей крэкс-пексовых грядок.
( Читать дальше )
Посты Атамана и Нео
- 24 апреля 2015, 09:03
- |
Время от времени эти посты кто то выкладывает, некоторые платно.
Старая тема на смартлабе: smart-lab.ru/blog/136886.php там их фоты и полно интересной инфы.
Для фанатов трейдинга которые ещё не знают.
Посты (Конспекты.rar, вверху стрелочка скачать) drive.google.com/file/d/0BzrzVQF_vqJDYUxXRGhFenppWVU/view?usp=sharing
Вечерний анализ Si от 23.04.15
- 23 апреля 2015, 23:30
- |
Поехали...
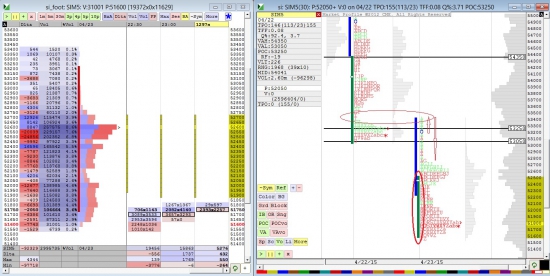
Поставлю картинку сразу. Вчера было узкое открытие дня, что давало подсказку о трендовом развитии. День действительно развился трендовый и показал «минус-развитие» в области, отмеченной овалом. Сегодня с открытия протестировали эту область и это место было хорошей точкой входя в короткую позицию. Короткий стоп, хорошая вероятность. После теста было хорошее движение с обновлением предыдущего дня. Область значения (вертикальный овал) ниже области значения предыдущего дня, что дает подсказку о дальнейшем снижении актива. Точка контроля (POC) так же внизу. Вверху отличный хвост продаж, составной день так же продажный. Объемы не перешли вниз, остались в середине дня. Не существенно, но в памяти держать стоит. Подсчет TPO говорит мне о завтрашнем открытии с обновлением минимумов сегодняшнего дня. С большой вероятностью продолжим дальнейшее снижение и завтра. Ожидаю актив на 48000 примерно. Хотя мне остановку и разворот покажет Market Profile. Всем хорошей торговли и профитов…
Дивиденды 2015
- 23 апреля 2015, 11:29
- |
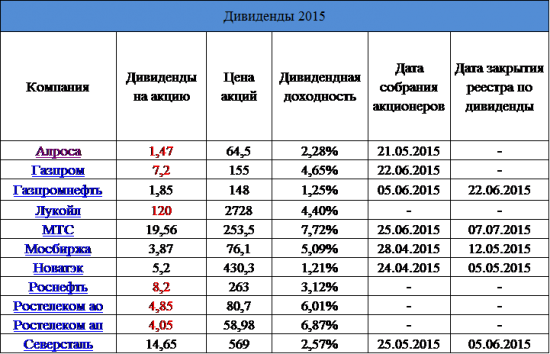
Красным выделены приблизительные дивы, рассчитанные исходя из прошлых выплат или из завления менеджмента .
Полный список по ссылке
Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
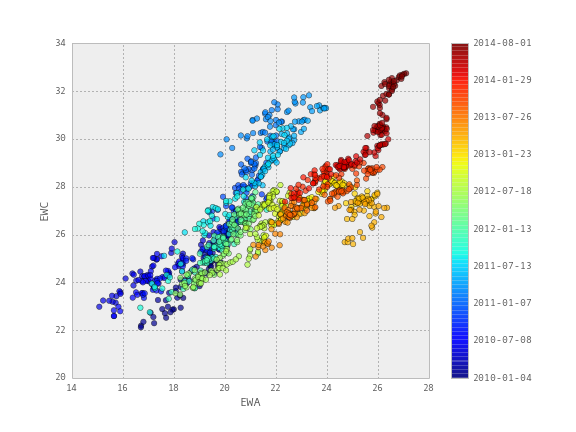
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
Методичка ABC от blastarr_no_1 "Основные принципы спекуляции" (часть 5)
- 23 апреля 2015, 09:24
- |
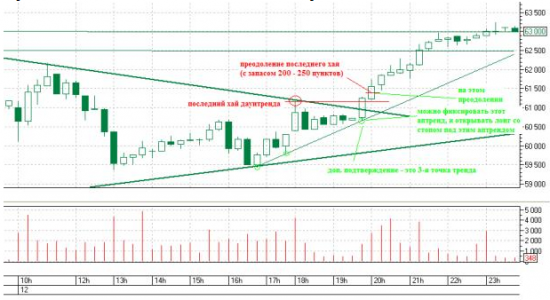
Следствие предыдущего пункта (про войну трендов) – часто в одну сторону идут тренды разной крутизны. Так вот, они независимы, и слом одного не отменяет прочих! Поэтому, например, если сломан только резкий даунтренд, это вовсе не значит, что надо покупать, т.к. есть еще и более старый, плавный
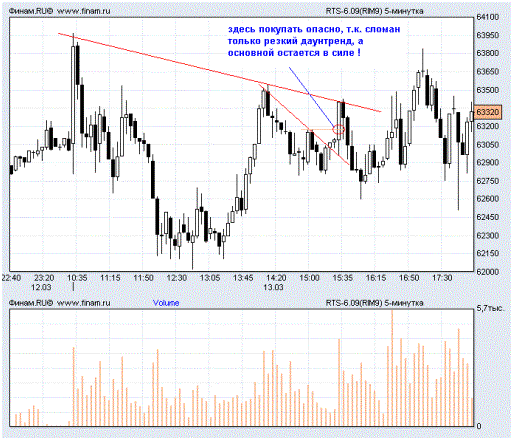
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал