Избранное трейдера gvv
НЕФТЪ - Глобальный взгляд
- 01 января 2017, 08:54
- |
Как то давно сделал прогноз, что в 2016 году
будет достигнуто дно по индексу РТС
основан прогноз был
на чётко работающих кредитных циклах в США
логика была основана на том что
новый кризис в экономике США неизбежно наступит в 2017 году
и чтобы не повторить кризис 2007-2008 г.г
США придётся на опережение начать стимулировать свою экономику
т.е в конце 2016 года или в начале 2017 года
в экономику США должны хлынуть сотни млрд.$ с вертолёта
через увеличение бюджетных расходов США
а значит в первом полугодии 2016 года
по индексу РТС должны были достигнуть дна
все это понимали по этому США и планировали начать 3 МВ
в первом полугодии 2016 года
т.е США планировали через ИГ нагнуть Россию, Европу и Китай
поэтому США и сбили СУ в ноябре 2015 года...
НО планы США провалились...
и тут повис вопрос о спасении экономики США
ибо без мировой войны
спасение экономики США в 2017 году
приведёт неизбежно к краху $
( Читать дальше )
- комментировать
- 86 | ★10
- Комментарии ( 12 )
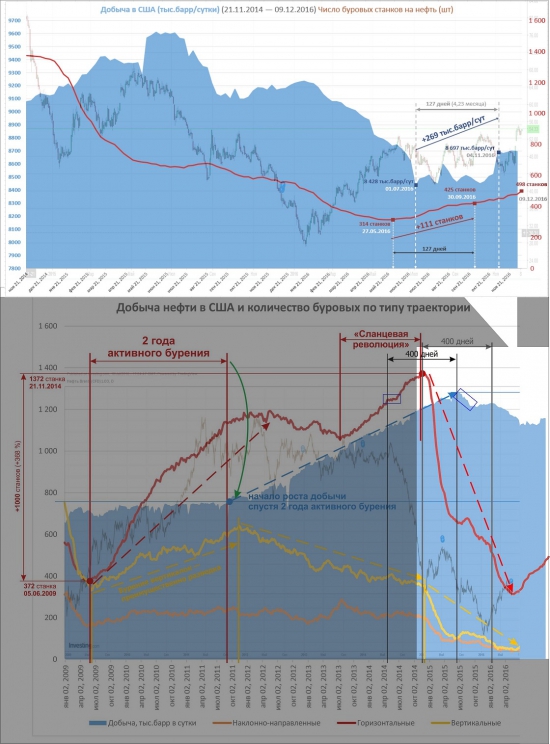
Нефть. Добыча в США и вышки по Baker Hughes.
- 10 декабря 2016, 22:04
- |
сохраню слова Романа
- 09 декабря 2016, 13:09
- |
— предвестник разворота — когда начинают пачками появляться
блоги о том, что это тренд и не надо идти против него
— блоги о том, что это тренд никогда не появляются в начале тренда
— блоги о том, что это тренд обычно пишут те, кто весь тренд его контртрендил, те же, кто стоит по тенду обычно ничего не пишут — им и так норм
— если тебе кажется, что акция слишком дорогая — это не повод ее шортить, а повод задуматься — почему покупателям так не кажется
— конца большого тренда почти никогда не бывает на границах каналов и других уровнях. Либо чуть выше, либо чуть ниже
— человек, утверждающий, что чего-то не бывает, либо дурак либо Бог
— на рынке деревья растут до небес и еще два дня
— если Вам кается, что рынок сейчас упадет, но шортить страшно, то он упадет. А если зашортили — то не упадет. Если шортить страшно, но зашорили — то упадет, но не добьет до тейка и вернется к стопу, а потом уже упадет.
( Читать дальше )
Теория. Соотношение «Доходность-Риск» золота (GOLD) в 2016 году
- 20 ноября 2016, 16:20
- |
В преддверии понедельника публикую свои расчеты по золоту по торговым дням 2016 года. Аналогичные расчеты по нефти см. здесь:
http://smart-lab.ru/blog/362367.php
http://smart-lab.ru/blog/363847.php
Результаты такие: средняя однодневная доходность (от закрытия сессии предыдущего дня к закрытию дня текущего) небольшая, но положительная: 0,056% или 14,1% в годовом исчислении (252 торговых дня).
Риск (волатильность), измеряемый средним отклонением, гораздо ниже (в 2,7 раза), чем у нефти и составляет за 1 сессию 1%, или 15,8% в год.
Потери (VaR) с вероятностью 95% не должны превысить 1,6% в день, а с вероятностью 99% — 2,3%. Если считать за T дней, эти величины нужно умножить на корень из Т.
Смещение в сторону риска есть, но не такое критичное, как у нефти. На первый взгляд кажется, что золото — инструмент менее рисковый и более приспособленный для долгосрочных инвестиций. Но есть свои нюансы, точнее «подводные камни»:
( Читать дальше )
Теория. Распределение дней роста/падения для нефти Brent в 2016 году
- 19 ноября 2016, 22:20
- |
На прошлой неделе рассчитал параметры доходности и риска в 2016 году по дням для нефти Brent по методикам RiskMetrics.
smart-lab.ru/blog/362367.php
Общий вывод был таков – риск (волатильность) инструмента на порядок превосходит небольшую, хотя и положительную текущую доходность. Ее проще всего получить на позиционных операциях (как в ту, так и в другую сторону) длительностью нескольких дней при жестком контроле рисков. Длительные инвестиции противопоказаны из-за чрезмерного смещения параметра «риск-доходность» в сторону риска.
Теперь возник вопрос – какой продолжительностью должны быть такие трейды? Т.е. исходя из статистического распределения, когда (точнее, с какой вероятностью положительного исхода) следует выходить из позы и занимать противоположную сторону?
Один из вариантов ответа – найти распределение периодов роста/падения, т.е. с какой частотой происходит непрерывный рост (и падение) 1-2-3-4 и т.д. дней подряд.
( Читать дальше )
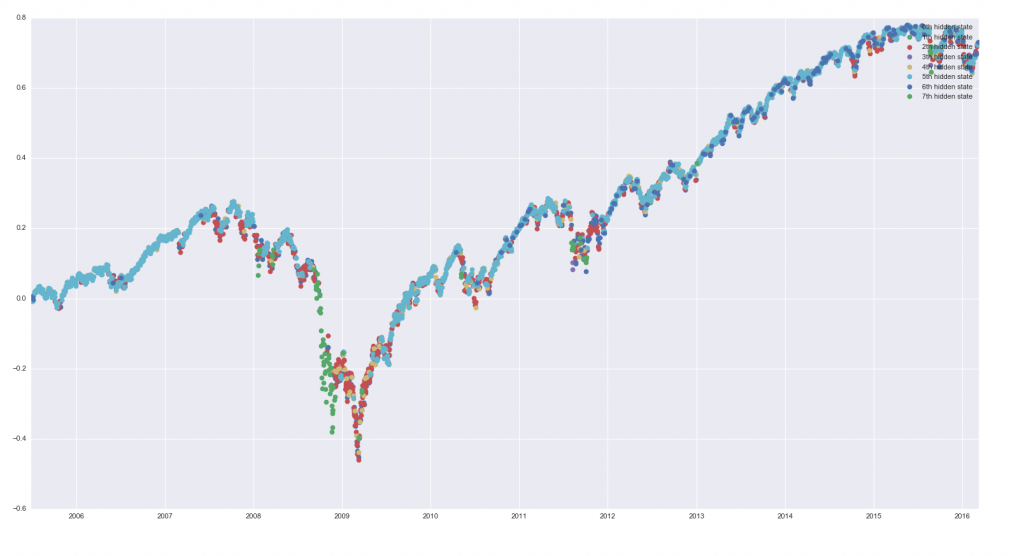
Состояния модели Маркова в графиках
- 06 августа 2016, 09:33
- |
Еще одна статья с ресурса www.talaikis.com по разработке простой стратегии на модели Маркова с использованием Python.
Модель скрытых состояний Маркова — это производительная, вероятностная модель, в которой последовательность наблюдаемых переменных генерируется некоторыми неизвестными (скрытыми) состояниями. Мы попытаемся найти такие неизвестные вероятностные функции для, скажем, S&P500. Все опишем кратко, без проверок на ошибки, без тестов вне выборки и т.д. Мы делаем это для того, чтобы минимизировать склонность к ненужному усложнению для начинающих. (Подробнее о модели Маркова см. на моем сайте — www.quantalgos.ru)
Что будем использовать:
библиотеку Python - hmmlearn.
1. Данные. Возьмем данные по свечам (OHLC), включающие объем, из нашей базы
( Читать дальше )
Brent - повтор 2015 ? )
- 09 июня 2016, 13:58
- |
коррекция от 1-2 в первый уровень фибовеера и шипом в 23.6 фибо уровня от 1-2
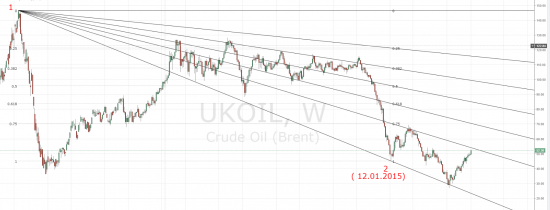
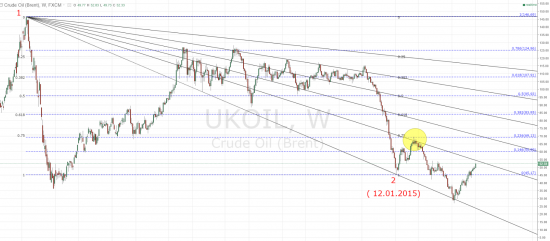
январь 2016
по правилам построения фибо двойку
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал