Избранное трейдера _sg_
Где лицензия ЦБ РФ?..
- 05 декабря 2018, 23:53
- |
Этот же вопрос, но уже более настойчиво, ставится и сейчас (См.: Главный финансовый аферист России. https://forum-msk.org/material/news/15224461.html ).
Наконец, на днях, вопрос этот был сформулирован еще более определенно: с позиций государственно-правовой и политико-уголовной точки зрения уже… ( См.: Михаил ДЕЛЯГИН. Не пора ли отозвать лицензию у Банка России? worldcrisis.ru/crisis/3224562 )
- комментировать
- ★1
- Комментарии ( 2 )
Корпоративные бонды под табу для частного инвестора!
- 05 декабря 2018, 17:14
- |
Почему я не рекомендую корпоративные бонды физическим лицам?
В своих выступления и обучающих материалах я всегда говорю, что физические лица должны сторониться вложений в корпоративные облигации. На то есть два простых основания:
- Риск дефолта
- Риск ликвидности
Но обычно, этих простых оснований недостаточно, чтобы убедить людей держаться подальше от «корпоратов». И чтобы показать, почему я решительно против, представляю вашему вниманию настоящую небольшую статью.
Начнём с основ. Из общего курса по инвестициям, мы знаем, что цена любой облигации определяется из простой формулы дисконтированных (приведённых) денежных потоков. При этом мы можем считать как стоимость облигации из нее, так и доходность к погашению (ставку дисконтирования) если нам известна цена на рынке. Формула 1:
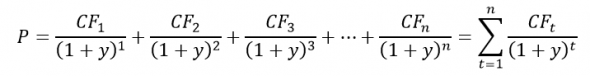
( Читать дальше )
Комментарий к комментариям
- 05 декабря 2018, 14:31
- |
Читаю комментарии к своим вчерашним сообщениям и не знаю уже, как реагировать. Вот пример:
“Если что-то выглядит как СВ, ведет себя как СВ и не содержит в себе обнаружимых закономерностей, то почему мы должны отказывать себе в удовольствии использовать наработки из теорвера и матстатистики?”
Смысл моих постов в обратном:
“Если что-то выглядит как СВ, ведет себя как СВ”, но на самом деле СВ не является, то “использование наработок из теорвера и матстатистики” ведет к проигрышу!
Излагать проще я не умею.
Но попробую
Вы наблюдаете за автомобилем, движущимся по Варшавскому шоссе в направлении области. После двух часов наблюдений по оценкам скорости и направления делаете статистически значимый вывод о том, что через трое суток автомобиль окажется в окрестности Варшавы. В районе Обнинска автомобиль останавливается, водитель забирает с дачи тещу и едет обратно в Москву. В чем ошибка? С точки зрения статистики все безупречно. Ошибка в предположении о случайном характере процесса.
( Читать дальше )
Визуализируя нестационарную нормальность
- 05 декабря 2018, 14:22
- |
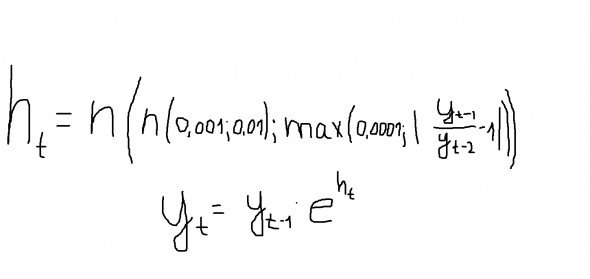
О воспроизведении каких феноменов идет речь? Это гэпы и шпили. 4 случайные реализации подряд:
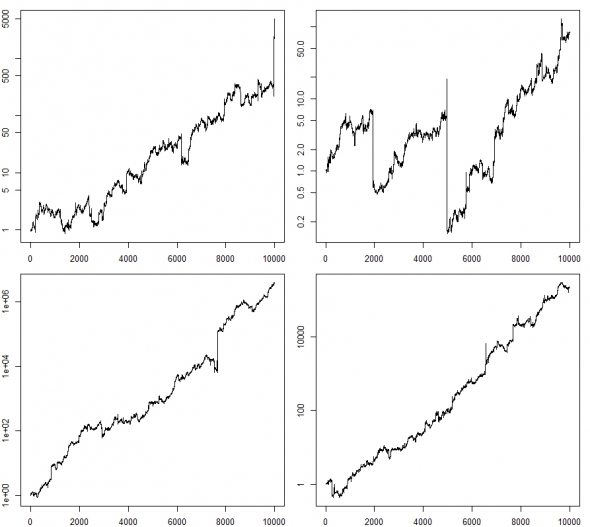
( Читать дальше )
Четвертая мировая война от А.В. Курпатова.
- 04 декабря 2018, 19:43
- |
Заглянул по старой памяти (с удовольствием читал его «Красную таблетку» и еще 2 книги этой трилогии) к Курпатову на «Сноб» и обнаружил, что он написал новую книгу.
Андрей Курпатов: Четвертая мировая война. Будущее уже рядом.
https://www.labirint.ru/books/668330/
Под третьей мировой войной понимается борьба с терроризмом, а четвертой обозначается идущая сейчас очередная промышленная революция (переход к 6-му технологическому укладу, России нужно прыгнуть в него сразу из 4-ого), в первую очередь в связи с искусственным интеллектом и ее кульминацией — технологической сингулярностью. Самообучившийся и самоорганизовавшийся, вышедший из-под контроля своих творцов, IT-гигантов типа Google, ИИ против людей.
К тематике Смарт-лаба прямо относится один из нарисованных Курпатовым сценариев 4-й мировой — «Биржевой апокалипсис».
Журнал «Сноб» опубликовал несколько отрывков из этой книги
( Читать дальше )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Вопросы 3,4.
- 04 декабря 2018, 16:30
- |
3. Оправдано ли использование логарифмического нормального распределения для описания терминального состояния базового актива
Можно догадаться, почему именно логнормальную модель распределения использовали Блэк и Шолес при решении задачи о нахождении справедливой стоимости опциона. Модель с гауссовыми приращениями брать было нельзя – она допускает уход цены БА в отрицательную область. Следующая, относительно простая логнормальная модель вполне годилась. Найденное на ее основе решение стало основой всей современной теории опционов.
Теперь ложка дегтя.
Мы предполагаем, что приращения цен акций, входящих в расчет индекса РТС, независимы и подчинены закону логарифмического нормального распределения. Поэтому при вычислении цен опционов на эти акции мы используем формулы БШ.
Но, согласно Центральной предельной теореме, из этого же предположения следует и то, что распределение приращений их линейной комбинации (то есть самого индекса РТС) должно быть близким к нормальному, тогда для расчета стоимости опционов на индекс РТС правильнее использовать формулу Башелье. Тем не менее, мы используем формулу БШ. Видимо, в расчете на то, что кривая волатильности все исправит.
( Читать дальше )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Второй вопрос.
- 04 декабря 2018, 16:11
- |
- 1. Что такое кривая волатильности и как она соотносится с моделью БШ
Все знают, что такое ожидаемая волатильность опциона (Implied Volatility). Это волатильность, которую нужно подставить в формулу Блэка-Шолеса, чтобы получить текущую рыночную стоимость опциона. Вычислив ее для всех страйков, можно затем аппроксимировать полученные значения гладкой параметрической кривой – кривой волатильности.
Но, если при расчете кривой волатильности мы всегда и везде используем формулу БШ, то мы так же всегда и везде должны доверять ее авторам, а они утверждали, что волатильность опционов должна в точности равняться волатильности базового актива, которая может быть только одна. Откуда взялась кривая? Либо мы верим Блэку и Шолесу (должна быть прямая), либо не верим (тогда кривая).
У кривой волатильности нет содержательного смысла. Это простая подгонка. Единственным ее назначением является устранение расхождений между теоретическими и рыночными ценами. Какую бы модель ценообразования опционов мы ни взяли, кривая волатильности исправит все ее огрехи. Что-то вроде толстого слоя штукатурки, с помощью которого можно выровнять любую стену.
При этом мы полностью лишены возможности отличить хорошую модель от плохой, после использования кривой расчетные цены любой модели будут близки к рыночным. Тогда почему мы пользуемся именно моделью БШ? Видимо, потому, что де-факто она признана стандартной.
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Первый вопрос.
- 04 декабря 2018, 15:55
- |
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов.
В теории опционов ключевую роль играет понятие теоретической или справедливой цены. Чем правильнее она рассчитана, тем выше шансы игрока на получение прибыли. Обилие математики в опционных расчетах убеждает, что именно профессиональные математики должны преуспевать в этой игре. Не ставя под сомнение последнее утверждение, сформулирую несколько вопросов, ответов на которые и сам, вообще-то, не знаю. Вопросы, тем не менее, важные. От ответов на них зависит, вправе ли мы использовать аппарат ТВиС при нахождении справедливых цен опционов.
1. Насколько оправдано использование математического ожидания при нахождении справедливой стоимости опционов
При расчете справедливой цены опциона (то есть цены, не дающей преимущества ни одной из сторон) используется соотношение:
MO[выигрыш продавца] = MO[выигрыш покупателя] = 0
Почему именно матожидание? Ответ вроде бы очевиден – потому что это самая содержательная и самая удобная из всех числовых характеристик случайной величины. Теперь рассмотрим пример.
( Читать дальше )
Визиализируем позы
- 04 декабря 2018, 14:38
- |
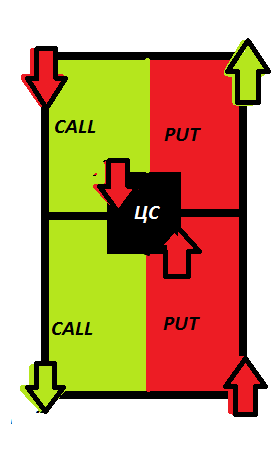
Так вот, чтобы не скиснуть, глядя в потолок я придумала для себя позу: за день два до экспиры просто открываю парные шорты:
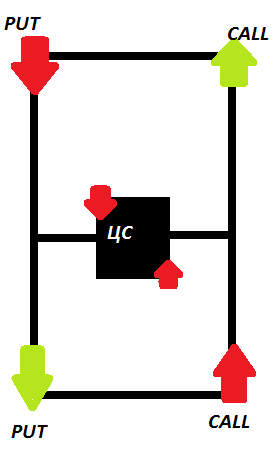
ЦС- центральный страйк
Красные стрелочки — это шорты
Зеленые стрелочки — лонги
А в целом картинка — доска опционов
Учитывая, что мы привыкли видеть Доску опционов в определенном виде и цвете, может картинка ниже будет более понятная:
( Читать дальше )
Мои итоги ноября: убыток октября закрыт
- 03 декабря 2018, 11:32
- |
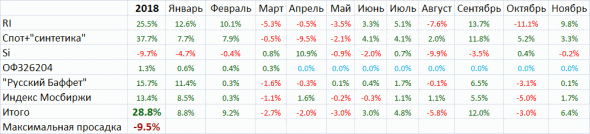
Ну собственно к сказанному в заголовке добавить нечего. О просадках говорить бессмысленно, так как только 29.11 был новый исторический максимум счета. По разным инструментам результаты в таблице.
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал

