Доброй ночи, коллеги!

Есть идея проверить текущие скиллы community на предмет умений в оптимизации / curve fitting.

Первый конкурс предполагается очень простой, поэтому приз — 5,000 руб. Но и задача простая. Можно и поднять ставку, но пока не ясно, зачем?

Есть массив минутных баров EURUSD длины, к примеру, 14400 баров (2 недели) и сколь угодно длинная предыстория для обучения (до 250,000 баров в целом. Думаю, будет более, чем достаточно))))
Требуется подобрать оптимальный линейный индикатор, который покажет максимум эквити.

Эквити маркетная, считается по формуле dEq(t) = (x(t)-x(t-1))*sign(ind(t-1))
Здесь t — время, x — цена
Эквити в целом = сумма приращений эквити (dEq(t)))
Индикатор ind(t) — линейная комбинация приращений цен до момента t (в будущее не заглядываем)
Глубина этой комбинации особо не ограничивается (см. ниже)

Задача — показать максимум эквити на тестовом участке

От участника требуется массив коэффициентов индикатора в формате csv определенной длины (любой до 16000, дабы можно было легко делать верификацию в Excel) и его понимание финреза стратегии на тестовой выборке. В случае аномально большого количества заявок можно ввести символическую плату (100 руб.?) за проверку данных, чтобы отсекать разную лажу. Возможно, я договорюсь с исполнителем и о меньшей цене, благо надо всего лишь вставить массив данных в таблицу и сравнить результат с анонсом. В любом случае, я лично этой хней заниматься не буду.

( Читать дальше )

Приветствую коллеги!
Решил поделиться своим финансовым планом.
Конечно в одном посте рассказать о нем просто не реально, но буду стараться.
Вот он:

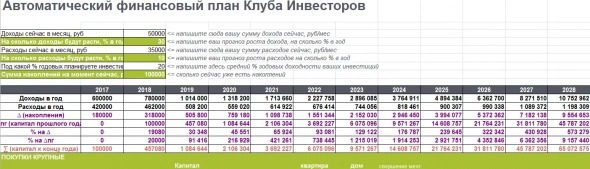
На момент составления у меня было только 100.000 в капитале (как я посчитал капитал записал отдельно видос).
Как такое возможно, что через 10 лет мы получили 65 млн рублей? Все очень просто! Сложный процент!
Конечно без него не имеет смысла стоить фин план, но есть еще некоторые сложности при его выполнении — это доходность капитала.
В своем фин плане она составляет 20% (конечно кто-то скажет что это много или мало, но это реально сделать).
Есть еще одна проблема — сколько сможете отложить.
Есть такое правило: расходы всегда превышают доходы.
Мне было очень сложно откладывать деньги, т.к как раз в 2017 году у меня был кризис в финансах. Конечно сейчас я это время вспоминаю с улыбкой, то тогда мне было не смешно(((

( Читать дальше )

Открыла в телеге экспериментальный канал, ориентирующий по внутридневной волатильности и дающий «пульс рынка» таким, каким видит его моя считалка реализуемой волатильности. Присоединяйтесь. Монетизироваться не будет. Рекламы не будет. Услуга предоставляется как есть. Все принимаемые Вами торговые решения — как и любые решения по жизни — как всегда на Вашей ответственности. Дискуссий не будет и флуда не будет — голые цифры в разрезе справедливая IV + справедливая цена связки на ЦС.
Данные обновляются три раза в день: в районе 9-00, в районе 15-00 и в районе 21-00. Стараюсь делать это регулярно и как можно ближе к означенным часам, но не всегда получается точно попасть во время.

Дисклеймер важный: приводимые данные тиковые и рассчитываются суточным окном. Трактовать можно так: если БА будет двигаться так, как он двигался предыдущие сутки — справедливая цена стрэддла при указанной дате экспирации будет вот такая, как написано. От управления это дело не освобождает ни разу. Прогноз, где что экспирируется — никакой не дается. Я придерживаюсь мнения, что цена опциона — это стоимость его хеджа. У кого другие воззрения на этот счет — имейте в виду.

( Читать дальше )

В личку спрашивают в каком банке лучше открыть вклад. 

Это точно форум трейдеров?))

Отвечу, как это делаю я.

1. Выбираю только системообразующий банк. Читаю отзывы на банки ру, сразу черный список — массовые кражи, блокировки счетов, отказы выплачивать ден средства.

2. Прихожу в офис банка, изучаю все документы. Проверяю реквизиты сторон.

3. Получаю на руки заверенный список всех документов, указанных в заявлении на открытие вклада, кроме тарифов. Если общий обьем документов более 30 листов, просто мило прощаюсь с операционистом и ухожу в другой банк.

4. Получаю заверенную выписку из тарифов — выплата ден средств с вкладов либо поступивших наличными без комиссии. Заверяется — выписка из тарифов (название банка), должность, подпись, дата, штамп.

5. Пишу заявления по ситуации, такого типа

1. Между мной и банком заключен договор КБО, в рамках которого банк уведомляет меня, что волен менять условия договора и тарифы в одностороннем порядке. На основании ст 16 ЗоЗПП и ст 168 ГК РФ, я возражаю против данного пункта договора и запрещаю банку менять условия договора и тарифы в одностороннем порядке.

( Читать дальше )

В этом посте я хочу рассмотреть вариант арбитражной стратегии, и протестировать его на чувствительность к проскальзыванию, чтобы понять возможность применения.

Далее будут приведены мои субъективные умозаключения.

Для начала перечислю виды арбитража, которые я знаю:

1. Арбитраж одинаковым активом между разными биржами. Сложность работы по этой технологии заключается в том, чтобы разместить торговый сервер между двумя биржами так, чтобы задержки пакетов между биржами были одинаковыми.
2. Арбитраж между активом и его деривативом.
3. Статистический арбитраж между коррелируемыми активами.
4. Календарный арбитраж.

Момент, который объединяет эти стратегии, состоит в том, что торговая позиция выставляется всегда одновременно по двум инструментам в противоположные стороны (если активы прямо скоррелированы, и в одинаковые стороны в ином случае).

Все эти арбитражные стратегии в основном относятся к классу рыночно-нейтральных «mean reversing» стратегий, потому что не следуют за трендом, а пытаются вернуться к некой справедливой цене актива (та же трендовая составляющая), выставляя позиции против отклонения от тренда, хотя, конечно, можно придумать и трендовые стратегии, использующие актив-«поводырь» для прогнозирования тренда.

( Читать дальше )

Это исследование я сделал под влиянием бурной дискуссии на форуме  о распределении «хвостов» приращений логарифмов цен, возникшей, казалось, на «пустом месте»: насколько корректны доверительные интервалы для оценок параметров линейной регрессии в альфа-бета модели?

Кроме указанной ссылки, дискуссия продолжилась в еще двух ветках: тут и тут.

Действительно, эти оценки в классическом случае строятся на основе центральной предельной теоремы для статистик оценок параметров линейной регрессии. Однако, как я уже писал на смартлабе, необходимым условием которой является скорость роста дисперсии суммы слагаемых как О(N), N – число слагаемых, а для быстрой сходимости в центральной области еще и требуется конечность абсолютного третьего момента любого слагаемого (если говорить о сходимости на всей прямой, включая «большие уклонения»,  то еще требуется  и конечность всех моментов отдельных слагаемых). Однако эти условия не выполняются для части распределений Парето и Стьюдента с полиномиальной скоростью убывания «хвостов» и поэтому для «хорошего» приближения суммы таких слагаемых нормальным законом требуется очень большое число испытаний, которых, как правило, в альфа-бета модели, построенной на дневных данных, нет. А значит традиционные методы построения доверительных интервалов для оценок параметров этой модели «не работают».

( Читать дальше )

Кто сейчас занимается всякой фигнёй — тот я.
Да и рынок благоволит:


В этот раз в идею фильтра легло наблюдение за дневками. Если они идут подряд ровненько на одном горизонтальном уровне, то там пила и хорошо бы эти места пропустить. Итого, берём несколько прошедших дней, в каждом дне имеем свой хай и лоу дня. Если минимум хаев ниже максимумов лоев за выбранные дни, то там, скорее всего, была пила. Этот фильтр и проверим на примере одной лонговой системы на РИ. Все расчеты различаются только количеством дней от 1 до 7. Очевидно, что при одном дне фактически фильтр не работает, поскольку максимум за один прошедший день всегда выше минимума за этот же прошедший день. Далее картинки.


( Читать дальше )

Привет! Сегодня не про результаты, а про методы. Закончил писать базовый функционал библиотеки для количественных исследований. Вот что из него можно выжать:

• Моделирование портфелей по кросс-секции и временным рядам;
• Квантильная методика формирования портфелей в % от выборки или фиксированное число инструментов;
• Возможность гибко задавать веса в портфеле по дополнительному фактору (почти smart beta);
• Можно вырывать данные для аналитики на каждом промежуточном этапе: сделки, размер позиций, комиссии, доходность портфелей;
• Возможность относительно точно учесть комиссионные расходы;
• Пока самая простая визуализация и метрики.

Как выглядит итоговая отрисовка:

Небольшая предыстория или зачем писать свой тестер

 

Не являясь базовым программистом, я пользовался готовыми решениями для бэктестов и особенно долго засиживался на платформе Quantopian. В прошлом году компания не получила нового транша от инвесторов и объявила о закрытии. Вместе с ней сгинул и весь написанный код, а знания синтаксиса несуществующей платформы близки по полезности к 1С-программированию при переезде в долину.
Поработав с другими сервисами, понял, что их существенные недостатки можно разделить на 3 группы:

( Читать дальше )

Портфельная теория Марковица

Портфельная теория Марковица(далее ПТМ) (Modern portfolio theory) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории.

Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.

Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.

( Читать дальше )

Я, вроде, уже писал подобный пост. Давно. Но, новое — хорошо забытое старое.
Очень многие неплохо владеют основами программирования, но написать DLL, связь через TCP или что-то другое для экспорта-импорта в Lua — это достаточно сложная процедура, и требует дополнительных знаний и много времени. Однако, если такую связь как-то по простому реализовать, то решились бы многие проблемы обмена данными с C#, Python и другими средами, и не надо вникать во всяческие C-API и прочие премудрости.
Однако, есть достаточно простой и доступный способ — обмен данными через файлы. Например, так:
1. программа Lua пишет строку (строки) данных в формате CSV в файл data.csv,
2. программа Lua создает пустой файл flag.ddd,
3. ваша программа проверяет наличие файла flag.ddd, что означает, что данные готовы к чтению,
4. при наличии файла flag.ddd программа читает данные файла data.csv и удаляет файл flag.ddd,
5. программа Lua проверяет наличие файла flag.ddd, и если этот файл отсутствует пишет строку (строки) данных в файл data.csv (см. п.1)
При обратном обмене происходит все тоже самое, только имена файлов другие.

( Читать дальше )