математика
Развернулся наш Рубль....
- 30 сентября 2022, 15:51
- |
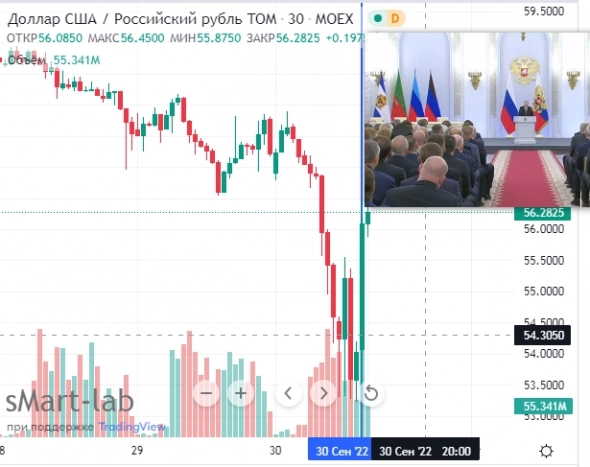
Посмотрите видос… все совпало. Особенно на речь. На вассалов, на гегемонию доллара.
Либо доллар запретят… либо он развернулся от 55.56

( Читать дальше )
- комментировать
- 688
- Комментарии ( 0 )
Что творится? Утренний обзор
- 20 сентября 2022, 10:09
- |

Доброе утро, всем привет!
Начнем сразу с хорошего. Чего тянуть-то. Со свеженького. Вот прям с печки. У бюргеров стата вышла — индекс цен производителей. Итак, по г/г (т.е. сейчас и год назад) — 45,8%!!! Прогноз был 36,1%. Месяц к месяцу же — 7,9% при прогнозе в 3,7%.
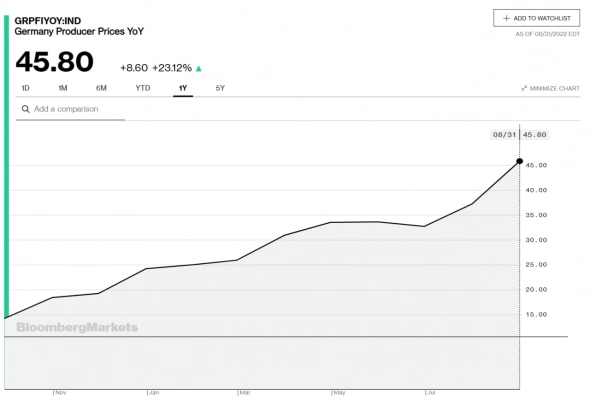
( Читать дальше )
Почему трейдеры любят кризисы, или как не умереть на бирже смертью храбрых?
- 01 сентября 2022, 12:05
- |
Чем хорош кризисный рынок и для кого он хорош?
Мне недавно задали вопрос, чем хорош кризисный рынок. И я решил поделиться в статье своим опытом, потому что за время торговли на бирже я видел не один кризис и его последствия. Кроме того, мне есть, что сказать о поведении самих трейдеров как в кризисную, так и в обычную фазы рынка.
Почему трейдеры любят кризисы?
На заре трейдинга в России появилась куча новых звезд. Все новые звезды на рынке формируются кризисными движениями. Скажем, первый сильный состав компании моей первой проп-компании был сформирован кризисом, если не ошибаюсь, 2008 года. Это дало некий скачок.

Если посмотреть на историю любой биржи, все посткризисные периоды — это растущая тенденция, которая продолжалась около 5 лет. И на таком рынке зарабатывает даже обезьяна. Например, возьмем рост доткомов. Когда появились такие компании как IBM, HP, Apple, они росли около 6 лет и на этой волне появились легендарные трейдеры — будущие инфоцыгане.
( Читать дальше )
Задачка по математике по мотивам Мальчика BuyBuy
- 11 августа 2022, 00:16
- |
3 бизнесмена прилетают на конгресс в небольшой городок. Они обнаруживают, что в мотеле осталась лишь одна комната, но в ней есть 3 кровати. Они решают остаться и разделить комнату на троих.
— Сколько стоит комната? — спрашивают они
— 30 долларов — отвечает клерк.
Бизнесмены скидываются по 10 долларов (10×3 = 30) и уходят.
Позже клерк обнаруживает, что комната на самом деле стоит 25 долларов, однако он не знает, как разделить остаток на 3 части. Он решает отдать по 1-му доллару каждому из бизнесменов (3×1 = 3), а 2 оставшихся положить к себе в карман (3 + 2 = 5).
Получается, что каждый из бизнесменов заплатил по 9 долларов (10 — 1 = 9).
Теперь: 3×9 = 27, плюс 2 доллара, которые присвоил клерк — получается 29.
Куда делся еще один доллар?
( Читать дальше )
Не замечай закономерности
- 04 августа 2022, 00:44
- |
Эти вопросы ожидают, что вы будете экстраполировать из конечного набора данных. Проблема в том, что, как и в приведенных выше цитатах, существует бесконечно много способов сделать это. Единственная разница между ними в том, что некоторые «чувствуют» себя более правыми, чем другие. Они интуитивно понятны, они “простые”. Но обе эти вещи на самом деле довольно субъективны. И поэтому, хотя эти вопросы претендуют на то, что имеют только один правильный ответ, на самом деле это не так.
Вот пример. Серия 1 2 3 5 …
Это может быть “все целые числа не более чем с одним коэффициентом”, то есть все простые числа и число 1 – тогда следующее число равно 7. Это также может быть последовательность Фибоначчи, но начинающаяся с 1 2 вместо 1 1 – тогда следующее число равно 8. Конечно, можно придумать бесконечно много правил для завершения этой последовательности. Другое простое правило — предполагать, что оно периодическое 1 2 3 5 1 2 3 5… — тогда следующее число — 1. Конечно, если бы вы смотрели только на первые три элемента в ряду, вы, вероятно, догадались бы, что следующее число — 4.
( Читать дальше )
Математический подход к оценке вероятности в трейдинге оказался не
- 23 июня 2022, 01:43
- |
ошибочным
Попытки анализа азартных игр привели к возникновению математического частотного подхода к расчету вероятности. Вероятности рассчитывались из серий экспериментов и являлись мерой случайности как эмпирической данности при условии того, что были известны наборы исторических данных.
Существует парадокс Бертрана, который гласит – вероятность любого случайного события не может быть чётко определена, пока не определён механизм или метод выбора размера случайной величины.
При сравнении двух гипотез на одних и тех же данных, теория проверки статистических гипотез, основанная на частотной интерпретации, позволяет отвергать или не отвергать модели-гипотезы. При этом адекватная модель может быть отвергнута из-за того, что на этих данных кажется адекватнее иная модель.
Вероятности, определяемые относительной частотой изменения случайного события при достаточно длительных наблюдениях исторических данных (например, цены), с построением моделей-гипотез её распределения, адекватны реальному миру с некоторой неизвестной степенью.
( Читать дальше )
Математические рассуждения о неправильности "риска собственной шкуры"
- 11 июня 2022, 09:27
- |
Представим себе абсолютно честную игру с вероятность получить выигрыш 50/50 — орлянку. Игроки выбирают сторону монеты и проигравший платит выигравшему 1 млн. руб. В эту игру решили сыграть богатый и бедный. Богатый начинает с 30 млн. рублей, а бедный с 10 млн рублей. Если у игрока заканчиваются деньги, то игра для него заканчивается.
Игра с двумя исходами является биномиальной и подчиняется законам распределения вероятностей.
Стандартное отклонение (степень изменения показателя выигрыша) составляет: 2 х Корень (100 х 0,5 х0,5 ) = 10 млн. руб.
Согласно нормальному распределению вероятность получить результат после 100 сеансов игры (бросков монеты) выигрыш или проигрыш в 10 млн. руб. составляет 68%. Вероятность выигрыша или проигрыша в 30 млн. руб. составляет 99,7%.
( Читать дальше )
Глубокое погружение в Мальчика (по просьбе Мальчика)
- 07 июня 2022, 22:29
- |
Никаких проблем. Однако, чтобы зрителям не было скучно, в текущем посте рассмотрим картинки не одного, а нескольких индикаторов:
1) на основе СЛАУ с одной переменной
indicator = d1 * (d1 / d2)2) на основе СЛАУ с двумя переменными (см. предыдущий пост)
indicator = d1 * (d1 * d4 - d2 * d3) + d2 * (d2 * d2 - d1 * d3)3) на основе СЛАУ с тремя переменными.
indicator = d1 * (-d1 * d4 * d6 + d1 * d5 * d5 + d2 * d3 * d6 - d2 * d4 * d5 + d3 * d3 * (-d5) + d3 * d4 * d4) /<br /> (-d2 * d4 * d6 + d2 * d5 * d5 + d3 * d3 * d6 - 2 * d3 * d4 * d5 + d4 * d4 * d4) +<br /><br /> d2 * (-d1 * d3 * d6 + d1 * d4 * d5 + d2 * d2 * d6 - d2 * d3 * d5 + d4 * d4 * d4) /<br /> (d2 * d4 * d6 - d2 * d5 * d5 - d3 * d3 * d6 + 2 * d3 * d4 * d5 - d4 * d4 * d4) +<br /><br /> d3 * (-d1 * d3 * d5 + d1 * d4 * d4 + d2 * d2 * d5 - 2 * d2 * d3 * d4 + d3 * d3 * d3) /<br /> (-d2 * d4 * d6 + d2 * d5 * d5 + d3 * d3 * d6 - 2 * d3 * d4 * d5 + d4 * d4 * d4)
4) на основе СЛАУ с 4 переменными (формулу смотреть в исходниках).
Пока, думаю, этого достаточно (если, конечно, Русский ВПК не укажет дальнейшее направление).
( Читать дальше )
Мальчик buybuy - я вас люблю (!) или ответ на пост "Рынок - это просто! Часть 3"
- 07 июня 2022, 04:12
- |
Формула индикатора в итоге свелась к
d(t) = d(t-1)*(d(t-1)*d(t-4)-d(t-2)*d(t-3)) + d(t-2)*(d(t-2)*d(t-2)-d(t-1)*d(t-3))
Для простоты обозначим d(t) = d, d(t-1) = d1, ...
итого имеем
d = d1 * (d1 * d4 — d2 * d3) + d2 * (d2 * d2 — d1 * d3)
Если d>=0, то покупка, иначе — продажа
1) Тикер BTSX.BTC_USD, 1 мин, 2015-2020 гг.
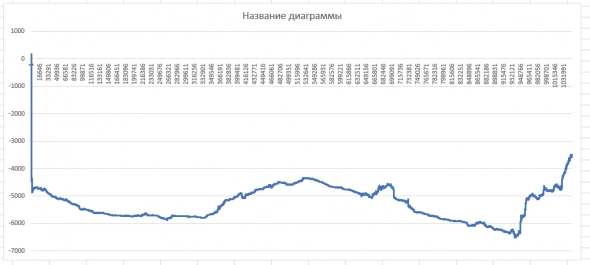
2) AUDCAD, DucasCopy, 2006-2021, 1 min
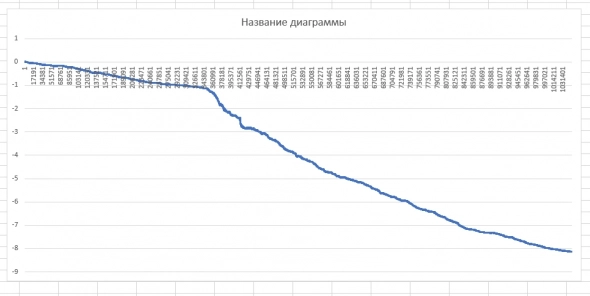
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
