Роботы

Вот тут smart-lab.ru/blog/248375.php Трейдер² наехал на Костю Гармалыгу, на мой взгляд, безосновательно.
Говорить о ничтожности стратегии можно, когда проведено полное и корректное бэк-тестирование на разных состояниях рынка.
А абстрактно сравнивать просадки без соотнесения с показателем риск/прибыль вообще нельзя.
Есть стратегии, которые берут 1000% прибыли на трейд. Но и вин/лосс у них соответственно, даже не 1 к 3.
Но на фига беспокоиться о слитом депозите, если, к примеру, на 5 слитых приходится один удесятиренный?
Всего лишь надо построить ММ чтобы дожить до такого удесятирения, и чтобы дисперсия не стерла со счета все средства.
Покупка очень дешевых опционов в расчете на очень редкое событие — один из примеров, но речь не об этом.

Речь о стейтментах (и результатах тестирования) которым можно верить.
Придумали стратегию, прогнали в тестере с учетом всех комиссий и проскальзываний, получили эквити:


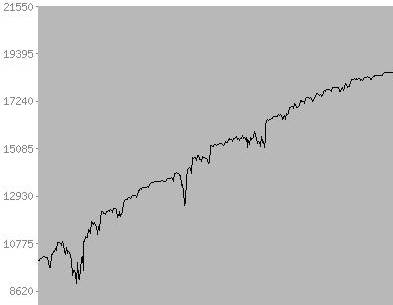
Период — полтора года, как я понимаю, по мнению многих — более чем достаточно.


( Читать дальше )

Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 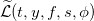, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 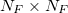, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях,  в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в

( Читать дальше )

Ребята, вот вы говорите роботы, hft и все такое. 

Но эти алгоритмы все анализируются, попадают в базы данных разработчиков софта, также есть риск что робот заглючит и будет лить депо либо на хвост роботу сядет кукл.

Либо этот алгорим станет известным и на нем начнут писать своих роботов уже разработчики софта и в итоге это все перестанет работать.

Вас волнуют эти проблемы? как вы их решаете?
 

Робот прошёл все тесты, и да мы его запустили на реальный счёт !

с 18-го числа наше детище заработало 60 % от начального депозита, гоняя всего 3 контракта по рынку ибо мы (не перечисленные ниже люди) нищеброды, ну ничего не поделаешь...

Отдельное спасибо !

Алексею Богатову (Ака доктор Богатов), моему учителю и ментору !!! http://smart-lab.ru/profile/Boggi/

Андрею Ерохину! Парень просто космос, оверинженер ! http://smart-lab.ru/profile/Doopler/

Саро Микаеляну! Человек не нуждается в представлении по определению !( кстати ждём релиза 2.0 ) http://smart-lab.ru/profile/Saro/

( Читать дальше )

Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ,  как достижение максимума следующего матожидания:

,

( Читать дальше )

В прошлой части мы рассмотрели оптимальное управление inventory risk в маркетмейкерском алгоритме. Напомню, что формулы для нейтральной цены и оптимального спреда между лимитными ордерами были получены при допущении, что цена следует геометрическому броуновскому движению. Управление inventory risk для моделей цены, более приближенными к реальности, рассматривается, например, в статье Pietro Fodra & Mauricio Labadie «High-frequency market-making with inventory constraints and directional bets» . Однако, применить напрямую на практике алгоритмы из этих статей вряд ли получится, так как в них  не учитывается действие adverse selection risk. Поэтому в данной части рассмотрим работу JIANGMIN XU «Optimal Strategies of High Frequency Traders», в которой автор делает попытку учесть этот вид риска, конечно, наряду с inventory risk.

( Читать дальше )

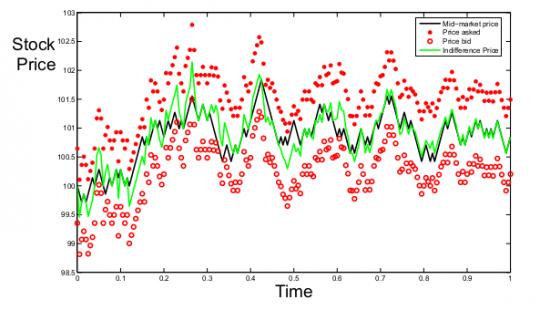
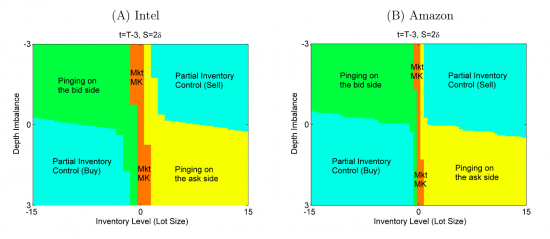
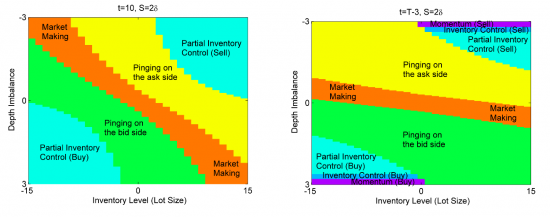
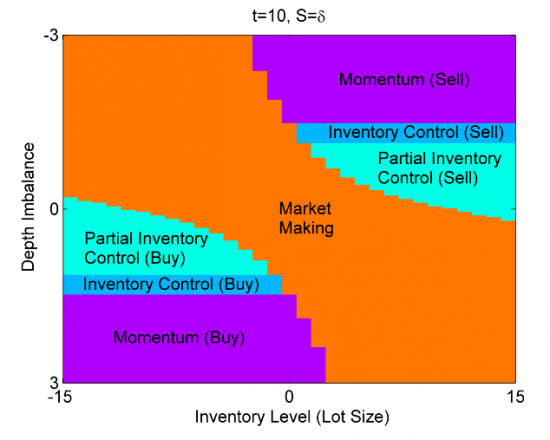
В биржевой торговле существует ряд алгоритмов, которые можно отнести к маркетмейкерским. Как правило, это означает выставление лимитных ордеров по обе стороны стакана, то есть как на покупку, так и на продажу, и целью такого алгоритма является получение прибыли от спреда - разницы между этими лимитными ордерами. Простейшая стратегия подобного рода — постановка ордеров одновременно на лучший бид и лучший аск — будет убыточной из-за действия следующих факторов:

1. Вероятность взятия ордера на стороне, противоположной движению цены в большинстве случаев выше, чем на стороне по направлению движения. То есть, если цена актива растет, то чаще будут исполняться ордера, выставленные на продажу, а ордера на покупку, соответственно — реже, в результате возникает убыточная позиция. В англоязычной литературе этот эффект называется

( Читать дальше )

Всем привет. Решил потестировать трансляцию торговли, для друзей и всех желающих)
 Это один из работающих серверов с роботами. Выставил в окне показ графика Si + информ-окна счета. В ближайшем будущем хочу, в качестве эксперимента, положить 100 тыр на отдельный счет, поставить туда несколько самых-самых роботов и попробовать стабильно разогнать этот счет. И сделать публичную трансляцию на каждый день) 
 Естественно, по ходу роста депо, кол-во ботов буду менять. Я не сижу на месте и постоянно что-то тестирую новенькое) Одних ботов буду убирать, других ставить, в общем быть инженером-управляющим)) А этот сервер будет моим личным полигоном для идей) 
 И да, Я ниразу не HFT. Пока не лезу в эту пучину, мне и свинговых идей и наработок хватает. Рабочий таймфрейм от м15 и выше.

Собственно сама трансляция через ютуб.



Еще возник вопрос по трансляциям через ютуб. Может кто знает, как долго там можно вести трансляцию и можно-ли ее вести круглосуточно?

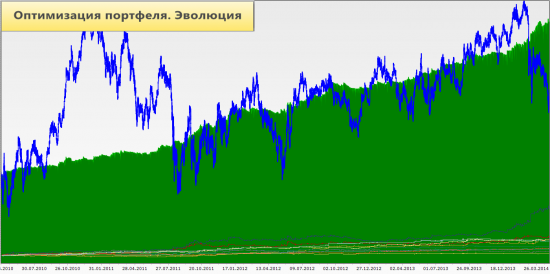
Для того, чтобы понимать о чем пойдет речь ниже отсылаю Вас к своему посту про PortfolioOptimizer на базе Wealth-lab.

PortfolioOptimizer — это оптимизатор с функцией автоматического сохранением TWR/HPR топа лучших результатов оптимизации. Термины TWR и HPR заимствованы из портфельной теории Ральфа Винса, к адептом которой я себя причисляю.
Для того, чтобы получить базовое понимание того, чем отличается теория Винса от классической портфельной теории, я также понятия TWR и HPR отсылаю Вас к книгам автора, или курсам на тему.
 

( Читать дальше )