вероятность
вероятность (probability) — число от 0 до 1, которое отражает шансы того, что случайное событие произойдет, где 0 — это полное отсутствие вероятности происхождения события, а 1 означает, что рассматриваемое событие определенно произойдет.
Вероятность события E является числом от до 1.
Сумма вероятностей взаимоисключающих событий равна 1.
эмпирическая вероятность — вероятность, которая посчитана как относительная частота события в прошлом, извлеченная из анализа исторических данных.
вероятность очень редких событий нельзя посчитать эмпирически.
субъективная вероятность — вероятность, основанная на личной субъективной оценке события безотносительно исторических данных. Инвесторы, которые принимают решения о покупке и продаже акций зачастую действуют именно исходя из соображений субъективной вероятности.
априорная вероятность -
Шанс 1 из… (odds) того что событие произойдет через понятие вероятности. Шанс появления события выражается через вероятность так: P/(1-P).
Например, если вероятность события 0,5, то шанс события 1 из 2 т.к. 0,5/(1-0,5).
Шанс того, что событие не произойдет вычисляется по формуле (1-P)/P
Несогласованная вероятноть — например в цене акций компании А на 85% учтено возможное событие E, а в цене акций компании Б всего на 50%. Это называется несогласованная вероятность. Согласно теореме голландских ставок, несогласованная вероятность создает возможности для извлечения прибыли.
Безусловная вероятность — это ответ на вопрос «Какова вероятность того, что событие произойдет?»
Условная вероятность — это ответ на вопрос: «Какова вероятность события A если событие Б произошло». Условная вероятность обозначается как P(A|B).
Совместная вероятность — вероятность того, что события А и Б произойдут одновременно. Обозначается как P(AB).
P(A|B) = P(AB)/P(B) (1)
P(AB) = P(A|B)*P(B)
Правило суммирования вероятностей:
Вероятность того, что случится либо событие A либо событие B —
P (A or B) = P(A) + P(B) — P(AB) (2)
если события A и B взаимоисключающие, то
P (A or B) = P(A) + P(B)
Независимые события — события A и B независимы если
P(A|B) = P(A), P(B|A) = P(B)
то есть это последовательность результатов, где значение вероятности постоянно от одного собятия к другому.
Бросок монеты — пример такого события, — результат каждого следующего броска не зависит от результата предыдущего.
Зависимые события — это такие события, когда вероятность появления одного зависит от вероятности появления другого.
Правило умножения вероятностей независимых событий:
Если события A и B независимы, то
P(AB) = P(A) * P(B) (3)
Правило полной вероятности:
P(A) = P(AS) + P(AS') = P(A|S')P(S) + P (A|S')P(S') (4)
S и S' — взаимоисключающие события
математическое ожидание (expected value) случайной переменной есть среднее возможных исходов случайной величины. Для события X матожидание обоначается как E(X).
Допустим у нас есть 5 значений взаимоисключающих событий c определенной вероятностью (например доход компании составил такую-то сумму с такой вероятностью). Матожиданием будет сумма всех исходов помноженных на их вероятность:
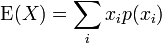 (5)
(5)
дисперсия случайной величины — матожидание квадратных отклонений случайной величины от ее матожидания:
s2 = E{[X — E(X)]2} (6)
условное матожидание (conditional expected value) — матожидание случайной величины X при условии того, что событие S уже произошло.
Вероятность события E является числом от до 1.
Сумма вероятностей взаимоисключающих событий равна 1.
эмпирическая вероятность — вероятность, которая посчитана как относительная частота события в прошлом, извлеченная из анализа исторических данных.
вероятность очень редких событий нельзя посчитать эмпирически.
субъективная вероятность — вероятность, основанная на личной субъективной оценке события безотносительно исторических данных. Инвесторы, которые принимают решения о покупке и продаже акций зачастую действуют именно исходя из соображений субъективной вероятности.
априорная вероятность -
Шанс 1 из… (odds) того что событие произойдет через понятие вероятности. Шанс появления события выражается через вероятность так: P/(1-P).
Например, если вероятность события 0,5, то шанс события 1 из 2 т.к. 0,5/(1-0,5).
Шанс того, что событие не произойдет вычисляется по формуле (1-P)/P
Несогласованная вероятноть — например в цене акций компании А на 85% учтено возможное событие E, а в цене акций компании Б всего на 50%. Это называется несогласованная вероятность. Согласно теореме голландских ставок, несогласованная вероятность создает возможности для извлечения прибыли.
Безусловная вероятность — это ответ на вопрос «Какова вероятность того, что событие произойдет?»
Условная вероятность — это ответ на вопрос: «Какова вероятность события A если событие Б произошло». Условная вероятность обозначается как P(A|B).
Совместная вероятность — вероятность того, что события А и Б произойдут одновременно. Обозначается как P(AB).
P(A|B) = P(AB)/P(B) (1)
P(AB) = P(A|B)*P(B)
Правило суммирования вероятностей:
Вероятность того, что случится либо событие A либо событие B —
P (A or B) = P(A) + P(B) — P(AB) (2)
если события A и B взаимоисключающие, то
P (A or B) = P(A) + P(B)
Независимые события — события A и B независимы если
P(A|B) = P(A), P(B|A) = P(B)
то есть это последовательность результатов, где значение вероятности постоянно от одного собятия к другому.
Бросок монеты — пример такого события, — результат каждого следующего броска не зависит от результата предыдущего.
Зависимые события — это такие события, когда вероятность появления одного зависит от вероятности появления другого.
Правило умножения вероятностей независимых событий:
Если события A и B независимы, то
P(AB) = P(A) * P(B) (3)
Правило полной вероятности:
P(A) = P(AS) + P(AS') = P(A|S')P(S) + P (A|S')P(S') (4)
S и S' — взаимоисключающие события
математическое ожидание (expected value) случайной переменной есть среднее возможных исходов случайной величины. Для события X матожидание обоначается как E(X).
Допустим у нас есть 5 значений взаимоисключающих событий c определенной вероятностью (например доход компании составил такую-то сумму с такой вероятностью). Матожиданием будет сумма всех исходов помноженных на их вероятность:
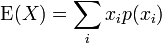 (5)
(5)дисперсия случайной величины — матожидание квадратных отклонений случайной величины от ее матожидания:
s2 = E{[X — E(X)]2} (6)
условное матожидание (conditional expected value) — матожидание случайной величины X при условии того, что событие S уже произошло.
Связанные статьи:
- 1 +8 16/09 дисперсия
- 17/09 асимметричное распределение
- +8 05/07 дерево вероятностей

















