Блог им. uralpro
Алгоритмы маркетмейкера. Часть 5
- 09 апреля 2015, 11:27
- |
Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 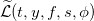 , в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью
, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 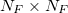 , где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
Далее, определение для матожидания квадратичного и линейного изменения цены:
![Алгоритмы маркетмейкера. Часть 5 \mathbb{E}_td[P,P]_t=(\frac{1}{4}\lambda^J_1+\lambda^J_2)dt](http://mathurl.com/pzvmwlp.png) , где
, где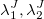 — интенсивность скачков цены на полшага и один шаг соответственно.
— интенсивность скачков цены на полшага и один шаг соответственно.
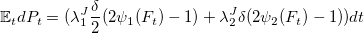 , где
, где 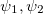 — вероятности скачков цены — см. часть 2.
— вероятности скачков цены — см. часть 2.
Оператор воздействия величины спреда на функцию владения:
![Алгоритмы маркетмейкера. Часть 5 \mathcal{L}^S\circ v(t,y,f,s)=\Bigg(\sum\limits_{j=1}^3 \rho_{ij}[v(t,y,f,j\delta)-v(t,y,f,i\delta)]\Bigg)\lambda^S](http://mathurl.com/lz5em3r.png) , где ρij- элементы матрицы переходов марковского процесса скачков спреда, λS- интенсивность этих скачков.
, где ρij- элементы матрицы переходов марковского процесса скачков спреда, λS- интенсивность этих скачков.
В выше приведенных формулах все интенсивности могут быть получены из рыночных данных путем простого расчета, например, можно подсчитать количество скачков спреда за определенный промежуток времени и параметр λS будет равен этому количеству, деленному на длительность промежутка в секундах. Интенсивности 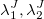 считаются аналогичным образом для скачков средней цены стакана на полшага и один шаг соответственно. Матрицу переходов тоже легко получить, подсчитав, сколько раз спред переходил из состояния один шаг цены в состояние два шага цены, из состояния один шаг цены в состояние 3 шага цены, и т.д., заполнив элементы матрицы ρi,j, где i означает начальное состояние спреда, j — конечное состояние спреда, на главной диагонали ρii=0. Приравняв сумму элементов в одной строке к 1, получим значенияρ, как доли от общей суммы ( элементы матрицы означают вероятности переходов).
считаются аналогичным образом для скачков средней цены стакана на полшага и один шаг соответственно. Матрицу переходов тоже легко получить, подсчитав, сколько раз спред переходил из состояния один шаг цены в состояние два шага цены, из состояния один шаг цены в состояние 3 шага цены, и т.д., заполнив элементы матрицы ρi,j, где i означает начальное состояние спреда, j — конечное состояние спреда, на главной диагонали ρii=0. Приравняв сумму элементов в одной строке к 1, получим значенияρ, как доли от общей суммы ( элементы матрицы означают вероятности переходов).
Вероятности скачков цены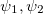 тоже найти несложно. Для этого нужно подсчитать количество скачков средней цены на полшага (для ψ1), попадающее в диапазон значений дисбаланса в каждом из интервалов [fj,fj+1], в каком-то промежутке времени, например, за один день, затем разделить величину в каждом интервале на общее число скачков. В результате получим плотность вероятности, интегрируя которую (складывая нарастающим итогом в численном варианте) в диапазоне всех значений дисбаланса f, получим исходные данные для нахождения формулы вероятности ψ1. Далее методом наименьших квадратов, используя эти данные, находим коэффициент β1 аппроксимирующей функции
тоже найти несложно. Для этого нужно подсчитать количество скачков средней цены на полшага (для ψ1), попадающее в диапазон значений дисбаланса в каждом из интервалов [fj,fj+1], в каком-то промежутке времени, например, за один день, затем разделить величину в каждом интервале на общее число скачков. В результате получим плотность вероятности, интегрируя которую (складывая нарастающим итогом в численном варианте) в диапазоне всех значений дисбаланса f, получим исходные данные для нахождения формулы вероятности ψ1. Далее методом наименьших квадратов, используя эти данные, находим коэффициент β1 аппроксимирующей функции 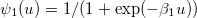 . Все то же самое проделываем для функции ψ2, только скачки цены берем на полный шаг. Таким же образом получаем формулы для вероятностей взятия лимитных ордеров в очереди заявок h(f) (см. часть 3), только подсчитывать будем количество исполненных ордеров (для бида и аска отдельно) в каждом интервале дисбаланса f.
. Все то же самое проделываем для функции ψ2, только скачки цены берем на полный шаг. Таким же образом получаем формулы для вероятностей взятия лимитных ордеров в очереди заявок h(f) (см. часть 3), только подсчитывать будем количество исполненных ордеров (для бида и аска отдельно) в каждом интервале дисбаланса f.
Нам осталось определить значения 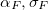 из уравнения Орнштейна-Уленбека для процесса дисбаланса объемов dFt (см.часть 2). Эти параметры находятся методом максимального правдоподобия, максимизируем следующую функцию:
из уравнения Орнштейна-Уленбека для процесса дисбаланса объемов dFt (см.часть 2). Эти параметры находятся методом максимального правдоподобия, максимизируем следующую функцию:
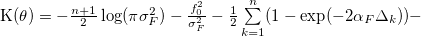
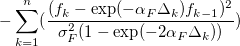
где fk — значение дисбаланса объема в момент времени tk,
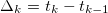 , n — общее число значений k.
, n — общее число значений k.
Итак, мы можем уже написать код для численного решения методом индукции. Ниже дан листинг на C#:
/* Функция решения уравнения HJB-QVI методом обратной индукции
* plt - структура, в которой определены основные переменные и политики
* plt.T - число временных точек расчета, plt.S - число значений спреда (=3)
* plt.F- число точек расчета дисбаланса объема, plt.Y - количество значений открытой позиции
* plt.dF - шаг величины дисбаланса объемов, plt.Fmax - модуль максимального значения дисбаланса
* plt.ticksize - минимальный шаг цены, plt.comiss - биржевая комиссия
* plt.w - массив значения численной функции владения
* plt.polmk - булевый массив, определяющий, какая политика будет использована при текущих значениях [t,y,f,s]
* если true - лимитные ордера, false - маркет ордера
* plt.thtkq - массив объемов маркет ордеров при действии политики маркет ордеров
* plt.thmka, plt.thmkb - массив значений 0 (выставление на лучшую цену) или 1 (выставление на шаг лучше лучшей цены)
* при действии политики лимитных ордеров
* maxlot - абсолютное максимальное значение открытой позиции
*/
public static void BackwardInduction(politics plt, int maxlot)
{
//Двигаемся вниз по временной сетке
for (int t = plt.T; t >= 0; t--)
{
//Двигаемся по сетке значения спреда
for (int s = 0; s < plt.S; s++)
{
// Определяем массив векторов оператора L (массив- по всем значениям открытой позиции,
//вектор оператора - по всем значениям дисбаланса)
double[][] L = new double[plt.Y][];
//Двигаемся по сетке открытых значений
for (int y = 0; y < plt.Y; y++)
{
// Инициализируем значения всех векторов L
L[y] = new double[plt.F];
//Вычисляем реальное значение открытой позиции из индекса
int yr = (int)(y - (plt.Y - 1) / 2);
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Реальное значение дисбаланса из индекса
double fr = plt.dF * f - plt.Fmax; ;
//Первый шаг - вычисление функции владения w в конечный момент времени T
if (t == plt.T) plt.w[y, f, s] = -Math.Abs(yr) * ((s + 1) * plt.ticksize / 2 + plt.commis);
else
{
//В остальные моменты времени находим значения векторов L (пока без умножения на
// дифференциальные матрицы в первой части выражения для L)
L[y][f] = LV(y, yr, fr, f, s, t, plt);
}
}
if (t < plt.T)
{
//Перемножение матричной части и векторов L, полученных выше, в результате получаем
// полностью рассчитанные вектора L. plt.rmatrix - матричная часть
matrixmlt(plt.rmatrix, ref L[y]);
}
}
//Вычисление выражения M*L для определения политики маркет ордеров
if (t < plt.T)
{
//Двигаемся по сетке открытой позиции
for (int y = 0; y < plt.Y; y++)
{
//Двигаемся по сетке дисбаланса объемов
for (int f = 0; f < plt.F; f++)
{
//Максимальное значение контрактов, допустимое в маркет ордере на данном шаге
int dzmax = Math.Min(plt.Y - 1 - y, maxlot);
double ML = -1000000;
//Двигаемся по сетке объема маркет ордера
for (int dz = Math.Max(-y, -maxlot); dz <= dzmax; dz++)
{
//Вычисление оператора M*L для каждого значения объема маркет ордера
if (L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis) > ML)
{
ML = L[y + dz][f] - Math.Abs(dz) * ((s + 1) * plt.ticksize / 2 + plt.commis);
//Занесение в политику маркет ордеров значения объема
plt.thtkq[t, y, f, s] = dz;
}
}
//Если оператор M*L больше оператора L при всех исходных параметрах, выбирается политика
//маркет ордеров
if (ML > L[y][f])
{
//Значению функции владения w присваивается значение оператора M*L
plt.w[y, f, s] = ML;
plt.polmk[t, y, f, s] = false;
}
// Иначе - политика лимитных ордеров
else
{
//Значению функции владения присваивается значение оператора L
plt.w[y, f, s] = L[y][f];
plt.polmk[t, y, f, s] = true;
}
}
}
}
}
}
}
//Функция вычисления значения оператора L, без перемножения на матричную часть
public static double LV(int y, int yr, double ft, int f, int s, int t, politics plt)
{
//Вычисление значений функции вероятности скачков цены на полшага и шаг psi1,2, с коэффициентами beta1,2
double psi1res = 0;
ClassMain.psifunc(plt.beta1, new double[] { ft }, ref psi1res, null);
double psi2res = 0;
ClassMain.psifunc(plt.beta2, new double[] { ft }, ref psi2res, null);
//Вычисление матожидания изменения средней цены, plt.lj1,plt.lj2 - интенсивности скачков цены
double Edp = plt.lj1 * (plt.ticksize / 2) * (2 * psi1res - 1) + plt.lj2 * plt.ticksize * (2 * psi2res - 1);
//Вычисление оператора воздействия спреда на функцию владения, plt.ro - матрица переходов состояний спреда
double Ls = 0;
for (int j = 0; j < plt.ro.GetLength(1); j++)
{
Ls += (plt.w[y, f, j] - plt.w[y, f, s]) * plt.ro[s, j];
}
//plt.ls - интенсивность скачков спреда
Ls = plt.ls * Ls;
//Вычисление матожидания среднеквадратичного изменения цены
double Edpp = (0.25 * plt.lj1 + plt.lj2);
double gv = -10000000;
int thmax = 1;
if (s == 0) thmax = 0;
double gvtemp = 0;
//Вычисление значений вероятности взятия лимитных ордеров в очереди заявок h(f)
//plt.ch - коэффициент в формуле для вероятности h(f)
double hresp = 0;
ClassMain.htfunc(plt.ch, new double[] { ft }, ref hresp, null);
double hresm = 0;
ClassMain.htfunc(plt.ch, new double[] { -ft }, ref hresm, null);
//Вычисление слагаемых ga и gb в выражении для оператора L, thmax - максимальное значение, которое принимает
// политика для лимитных ордеров - 1
for (int i = 0; i <= thmax; i++)
{
for (int k = 0; k <= thmax; k++)
{
gvtemp = (i * (plt.lMa) + (1 - i) * plt.lMa * hresp) * (plt.w[Math.Min(y + 1, (int)(2 * plt.Ymax)), f, s] - plt.w[y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * i) +
(k * (plt.lMb) + (1 - k) * plt.lMb * hresm) * (plt.w[Math.Max(y - 1, 0), f, s] - plt.w[y, f, s] + (s + 1) * plt.ticksize / 2 - plt.ticksize * k);
//Занесение значения 0 или 1 в политику лимитных ордеров
if (gvtemp > gv)
{
gv = gvtemp;
plt.thmkb[t, y, f, s] = i; plt.thmka[t, y, f, s] = k;
}
}
}
//Вычисление значения оператора L (без умножения на матричную часть)
//plt.dt- шаг времени, plt.gamma - мера риска
double lv = plt.w[y, f, s] + plt.dt * yr * Edp + plt.dt * Ls - plt.dt * plt.gamma * yr * yr * Edpp + plt.dt * gv;
return lv;
}
И приведу отдельный листинг вычисления матричной части выражения для оператора  :
:
//Вычисление матричной части выражения оператора L
public void MatrixSolve()
{
//Дифференциальные матрицы D1,2 и матрица идентичности I.
double[,] D1 = new double[F, F];
double[,] D2 = new double[F, F];
double[,] I = new double[F, F];
//Заполняем матрицы на сетке F x F
for (int i = 0; i < F; i++)
{
int k = 0;
if (i <= (F - 1) / 2) k = i;
else k = i - 1;
D1[i, k] = -1 / dF; D1[i, k + 1] = 1 / dF;
if (i == 0)
{
D2[i, i + 1] = 2 / (dF * dF);
}
else if (i == F - 1)
{
D2[i, i - 1] = 2 / (dF * dF);
}
else
{
D2[i, i - 1] = 1 / (dF * dF);
D2[i, i + 1] = 1 / (dF * dF);
}
D2[i, i] = -2 / (dF * dF);
I[i, i] = 1;
double Ft = dF * i - Fmax;
//Вычисляем значения матричной части выражения оператора L
//cft[1] - значение sigmaF из уравнения Орнштейна-Уленбека для Ft,
//cft[0] - значение alfaF
for (int j = 0; j < F; j++)
{
rmatrix[i, j] = I[i, j] - 0.5*dt * cft[1] * cft[1] * D2[i, j] - dt * cft[0] * Ft * D1[i, j];
}
}
alglib.matinvreport rep;
int info;
//Инвертируем матрицу, используя стороннюю библиотеку alglib
alglib.rmatrixinverse(ref rmatrix, out info, out rep);
}
На этом цикл статей по алгоритмам маркет мейкера завершен. Прошлые части статьи — в моем блоге или на сайте. Можно ли применить рассмотренную стратегию в реальной торговле? Несомненно, да. Вместо дисбаланса объема F возможно применение и других, более сложных сигналов, сохранив у них следование процессу Орнштейна-Уленбека, что не изменит нахождение параметров процесса. И в таком случае получим несколько разных HFT алгоритмов со всеми их преимуществами. Насколько хорошо дисбаланс объемов предсказывает цену исследовал пользователь r0man на моем сайте на примере фьючерса Si, за что ему огромная благодарность, вот что у него получилось:
На оси ординат — доля правильных предсказаний (вероятность), на оси абсцисс — количество тиков цены с момента замера дисбаланса. Таким образом достоверно утверждение о возможности предсказания цены актива в зависимости от дисбаланса объема в стакане.
Буду рад вашим отзывам по данным статьям и указаниям на ошибки, если таковые присутствуют в тексте.


теги блога uralpro
- ARIMA
- data feed
- ETF
- FORTS
- GARCH
- HFT
- IQFeed
- mean reversion
- momentum
- python
- S&P500
- VIX
- VPIN
- алгоритм
- алгоритм торговли
- алгоритмическая торговля
- алгоритмы
- алгоритмы торговли
- алготрейдинг
- альфа-сигналы
- андрей мовчан
- Биржевые роботы
- биткоины
- Блэк-Шоулз
- бэктестинг
- возврат к среднему
- волатильность
- высокастотники
- высокая доходность
- высокочастотная торговля
- высокочастотный трейдинг
- генетические алгоритм
- генетические алгоритмы
- гэп
- доходность трейдеров
- импульс
- импульсная система
- индексы
- интервью
- итоги
- итоги 2016
- Итоги 2018
- книга заявок
- коинтеграция
- колокейшн
- Конференции смартлаба
- конференция
- корреляция
- криптовалюта
- лчи
- маркет дата
- маркет мейкер
- марковиц
- марковский процесс
- математические модели
- машинное обучение
- модели
- Модели рынка
- модель
- модель Маркова
- Оптимизация портфеля
- опционные модели
- опционы
- Парный трейдинг
- парный трейдинг
- подготовка данных
- поток ордеров
- Публикации
- публикация
- разработка алгоритма
- разработка торговых систем
- раундтрип
- регрессия
- результат торговли
- робот
- роботы
- роботы в биржевой торговле
- скользящая средняя
- стакан
- стоп лосс
- стратегия
- торговля волатильностью
- торговые алгоритмы
- торговые стратегии
- улыбка волатильности
- ФОРТС
- Херст
- эквити
- язык R



















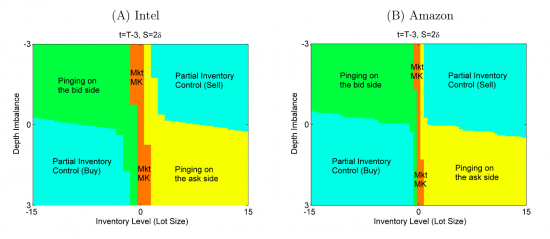

На приведенном в статье графике порог дисбаланса зафиксирован, а интервал предсказания меняется. Построен он лишь для того, чтобы понять применим ли алгоритм вообще и на каких промежутках времени. Сам же алгоритм работает (должен работать) немного тоньше и расчитывать оптимальные параметры дисбаланса для каждого момента времени, для каждого значения спреда, для каждой стратегии входа, выхода в зависимости от открытой позиции.
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 3.00 8.00 12.74 17.00 355.00: