Избранное трейдера wyg
Результат портфеля стратегий в мае 2015 года
- 06 июня 2015, 11:18
- |

С января 2013 года общая доходность составила +230.81% с максимальной фактической просадкой в пределах 15%. Параметр отношение доходности к максимальной просадке за все время составил порядка 15, что говорит о высокой эффективности выбранного подхода к управлению капиталом. Также стоит отметить, что состав стратегий в портфеле постоянно меняется. Идет разработка и внедрение новых систем, портфель становится все более сбалансированным. Уже действующие стратегии регулярно мониторятся на предмет соответствия реальных и тестовых параметров. В случае поломки стратегия удаляется из портфеля. В настоящий момент в портфеле около 16 различных стратегий, почти все работают на разных принципах и инструментах. Что дает неплохую диверсификацию даже на нашем достаточно небольшом рынке. Также в работе практикуется алгоритм снижения/увеличения объема в зависимости от сезонного фактора. Например, в летнем периоде спада активности объем несколько снижается. А в периоды, когда существует высокая вероятность увидеть рост волатильности и хорошее направленное движение — объемы соответственно немного увеличиваются.

Ровно два года назад было озвучено предположение о начале мощного «алгоцикла». Сейчас уже очевидно, что оно было верное, и мы до сих пор в нем. Рынок продолжает радовать. Всем удачных торгов!
- комментировать
- 42 | ★5
- Комментарии ( 12 )
Почему золото
- 02 июня 2015, 13:13
- |
частенько начали задавать вопрос — почему торгую только один инструмент — в частности сейчас золото.
отвечаю:
моя система анализа работает сразу со всеми таймфреймами
этапы анализа:
1 — обязательно начиная с ВЫСОКИХ тф и спускаясь ниже, строятся уровни и определяются модели движения.
1.1 — определив модель движения на одном ТФ я рисую потенциальный вектор этого движения
1.2 — перехожу на меньший тф
2 — на меньшем тф, построив уровни и определив по ним модель движения, так же определяю потенциал вектора.
2.1 — полученный потенциал сравниваю с потенциалом более высокого тф и корректирую общую потенциальную модель движения для двух тф
2.2 — перехожу на еще меньший тф
3… делаю все тоже самое для всех остальных таймфреймов спускаясь по ним до 5 минуток включительно.
в итоге у меня получается некая мождель общего потенциального движения расписанная чуть ли не на пару месяцев вперед.
( Читать дальше )
о стабильной доходности на бирже, безрисковые стратегии
- 19 мая 2015, 09:35
- |
С опытом торговли что-то вроде 20 лет, со стабильной доходностью около 30% годовых.
Показываю.
update: тут каждый второй комментатор пишет мне что типа RI в шорт, Si в лонг — это не арбитраж, а автор м&дило.
Сначала прочитайте статью, и я не говорю что это арбитраж, и это не я так делаю. Это лишь как один из вариантов берзисковой стратегии, о чём написал ниже один из капитанов. Разъясняю для совсем долбодятлов — безрисковой для управляющего, но не для инвестора. Основано на реальных событиях, к сожалению. И про нефть- я также не говорил нигде что это безрисковая страта и никому её не советовал.
Берём в ДУ.
RI в шорт, Si в лонг. Обратите внимание на направление, я не ошибся.
На следующий день имеем просадочку. Что делать? Усредняемся.
Ждём. Оп. Через 10 дней просадочка 18.7% от счёта.
С инвестором оговорена макс просадка 15%. Инвестор забирает деньги.
Как бонус. Инвестор спрашивает «как так?» и просит вернуть хотя-бы 3.7% разницы. Получает ответ типа (мой литературный перевод): «еб@ть ты лошара». Подробности тут http://smart-lab.ru/blog/255492.php
Воистину, для управляющего торговля была безрисковой и прибыльной.
А теперь поговорим серьёзно, хотя… прошлый абзац ведь тоже был серьёзный, смешного в нём мало.
( Читать дальше )
Модель скрытых состояний Маркова. Часть 3
- 18 мая 2015, 14:01
- |
В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый — использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.
Метод первый — одна модель с несколькими состояниями.
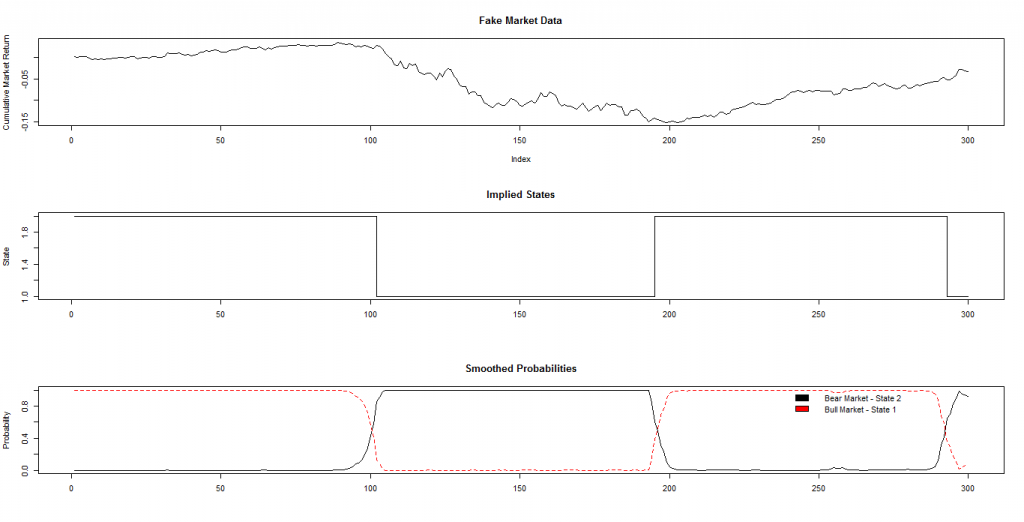
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu — медиана, sigma — среднеквадратичное отклонение. Распознавание будем производить для двух режимов — бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых — из медвежьего и 100 последних — из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):
( Читать дальше )
Первая правдивая КЛАССИФИКАЦИЯ ТРЕЙДЕРОВ
- 16 мая 2015, 10:22
- |
Третья Силы сторона есть, юный падаван. И говорит и знает мало о ней кто. Ведь профессиональная деформация программистов скромность тех джедаев не позволяет выставлять себя идиотами, неся бред.
Наблюдая идеологические войны «Разумного Инвестора» с ордой фриков рисующих палочки «Спекулянтами» создаётся впечатление что никаких других способов трейдинга не существует. А это мягко говоря не так.
Давайте вместе попробуем разбить трейдеров на группы. А затем объективно и беспристрастно посмотрим на эти группы поближе.
План:
- Разбить трейдеров на группы
- Про Тех Анализ
- Про Инвесторов
- Про Алготрейдинг
( Читать дальше )
Модель скрытых состояний Маркова. Часть 2
- 14 мая 2015, 13:34
- |
В предыдущей статье мы говорили об эффективных алгоритмах, необходимых для вычисления вероятностей и стат. распределений модели Маркова, которыми являются форвардный алгоритм и алгоритм Витерби. Форвардный алгоритм вычисляет вероятность соответствия данных наблюдения полученным моделью всем возможным последовательностям состояний. Алгоритм Витерби вычисляет вероятность соответствия данных полученной моделью одной, наиболее вероятной, последовательности.
В этом посте будет много формул, но без этого не обойтись, чтобы создать хорошую стратегию, надо разбираться в математической модели, лежащей в ее основе. Следующие части будут более приближенными к практике.
Форвардный алгоритм.
Форвардный алгоритм позволяет эффективно рассчитать функцию вероятности p(O|λ). Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
( Читать дальше )
Модель скрытых состояний Маркова. Часть 1
- 12 мая 2015, 14:35
- |
В данном цикле статей начинаем рассматривать модель Маркова, которая находит применение в задачах классификации состояния рынка и используется во многих биржевых роботах. Статьи основаны на постах, опубликованных в блоге Gekko Quant. Также будет рассмотрены практические алгоритмы на финансовых рынках. Код в цикле приведен на языке R. Вначале будет много теории, ее надо хотя бы попробовать понять, затем разберем практические примеры.
Рабочая среда распознавания основных паттернов.
Рассмотрим набор признаков O, полученный из набора данных d и класс w, обозначающий наиболее подходящий класс для O:
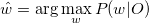
( Читать дальше )
Хороший сетап на покупку доллара.
- 07 мая 2015, 18:57
- |
Согласно моему видению, инвесторы предпочитают длинные выходные пересидеть в долларах.
Плюс упавшая нефть.
Разволновка по Эллиоту дает хороший вариант для входа по текущим, стоп можно разместить на минимуме вчерашнего дня — 50300.
Итого имеем: 50705 текущая на клиринге цена, риск 400 пунктов.
Если заходить частями, то можно не сильно рисковать.
И учтите возможность утреннего гэпа!
Спокойной всем вечерки!
P.S. Тейк по сетапу — держать до экспирации, ожидаю увидеть доллар в районе 60 р к тому моменту, т.е. 10000 пунктов.
Отношение прибыль / риск = 10000 / 400 = 25
Уже начал набор позиции.
Если выбьют по стопу, буду искать точку для перезахода.
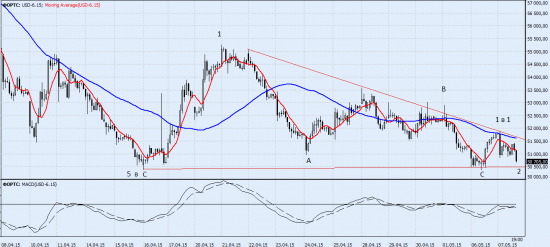
Секрет индикатора MACD
- 29 апреля 2015, 18:40
- |
Я знаю, что на данном рисурсе присутствуют в основном фондовые трейдеры, но индикатор MACD вещь универсальная. Ну, то есть строится он на основе скользящих, а скользящие в свою очередь на основе данных со свечей, поэтому можно резюмировать что работает он и под форекс и под фондовый рынок. Ну, я думаю это вы и так знаете)
Так или иначе хочу поделиться одной находкой, которую я узнал про этот индикатор. На евро баксе для дневных и недельных графиков похоже на чудо. На фондовом не тестировал, но очень интересно ваше мнение на эту тему. Видео прилагается.
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал