Избранное трейдера Andrew Volosnikov
Священный ГРААЛЬ N 2
- 11 июля 2019, 17:15
- |
Узнал о трейдинге от брата в 2014 году.Он тогда познавал его в интрадейной торговле на Si и Ri.Получалось у него не очень, уровень знаний был слабоват и упорства не было.Лично я тогда заразился.Смотрел ролики Резвякова, тогда они вдохновляли.Только в 2016-2017 году, я осознал что это вода конкретная.Брокерский счет открыл в 2016 году в Сбербанке.Поначалу 1-2 контракта гонял.Получалось относительно неплохо(помню как-то за день 1300р с 1 контракта снял).На радостях уволился с работы и залил еще немного денег.Затем пошли ошибки и пересиживание убытка.В итоге через 4 месяца бессистемной дрочки, пришлось пойти на работу и временно завязать с трейдингом(просадка оказалась 25%, ну и часть денег ушла на жизнь).Через полгода опять решил залить денег, показалось что опять грааль нашел.Через 2 месяца в состоянии эйфории опять уволился и история с просадкой повторилась вновь.
( Читать дальше )
- комментировать
- 9.9К | ★153
- Комментарии ( 55 )
Как торгуют Price Action профессионалы...
- 03 июля 2019, 20:18
- |
Итак, небольшая вводная часть. Я видел эту стратегию у нескольких людей. Во первых, начну с наиболее здесь известного человека это А.Герчик (да-да знаю многие считают его разводилой здесь, но пожалуйста дочитайте до конца пост прежде чем сделать выводы). В его терминах это торговля от «зеркального уровня на отбой». Пожалуйста посмотрите видео Герчика или просто дочитайте пост до конца. Дальше будут примеры.
По данной стратегии торговал профессиональный трейдер проп-фирмы Futex Том Дант (это the_Wizard из James16 для тех кто в теме). И вот здесь он подробно описывает эту стратегию (и тот факт что его научили так торговать в лондонском пропе). Вот ссылка https://www.forexfactory.com/showthread.php?t=287794. Если Вы стремитесь понять, что такое price action пожалуйста ОБЯЗАТЕЛЬНО пройдите по ссылке и прочитайте второе сообщение от Тома (the_Wizard) можно даже с гугл-транслейтом. Там вся суть того что вовсе не пин-бары есть прайс экшен и что когда Вы входите по Вашим формациям типа пин-бара или внешнего бара, то профи у же в прибыли и когда Вы только начинаете получать прибыль, то могут уже закрывать сделки.
( Читать дальше )
Качаем данные Питоном: Всемирный банк
- 25 мая 2019, 12:40
- |
Полная документация (в этом посте она не понадобится)
---
Если вы не хотите программировать, то и не надо. Все данные можно получить и без питона и построить красивый график:
Вот, к примеру, ВВП России и Италии:
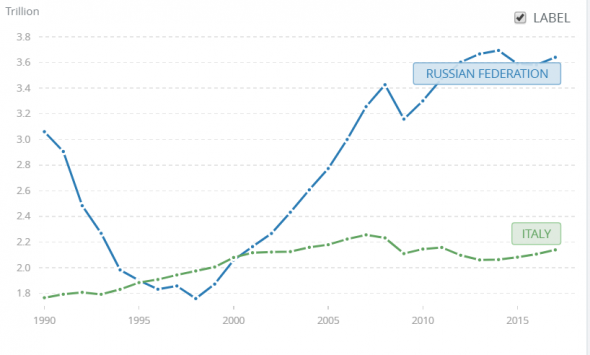
Ссылка на этот показатель. Там можно выбирать любые страны.
Но мы пойдём другим путём! Сложным! Этот путь позволяет строить графики любого вида и анализировать данные так гибко, как только вы захотите.
На выходе у нас получится такой график: ВВП по паритету крупнейших 10 стран мира. Скрипт сам понимает, какие страны крупнейшие:
( Читать дальше )
Как инвестировать в гособлигации
- 05 декабря 2018, 19:54
- |
Любые вложения в ценные бумаги — это риски. Их уровень инвестор выбирает сам, покупая определенные активы и составляя из них портфель. Гособлигации, или госбонды, — инструмент, который подходит разным инвесторам. Он может быть низкорискованным или высокодоходным — это зависит от государства-эмитента и особенностей самой бумаги.
Рассказываем, как выбрать подходящие гособлигации и где их купить.
Как выбирать гособлигации
В основном на цену облигаций и их доходность влияют рейтинг государства-эмитента, тип бондов и срок до их погашения, ключевая ставка в стране и ситуация на рынке. Рассмотрим каждый фактор подробнее:
Кредитный рейтинг государства. Присваивают его международные рейтинговые агентства — Moody’s, Standard & Poor’s (S&P), Fitch, DBRS. Происходит это так: они анализируют финансовое положение эмитента и текущую задолженность, оценивают будущие доходы, сравнивают с конкурентами, а потом выдают рейтинг.
( Читать дальше )
Корпоративные бонды под табу для частного инвестора!
- 05 декабря 2018, 17:14
- |
Почему я не рекомендую корпоративные бонды физическим лицам?
В своих выступления и обучающих материалах я всегда говорю, что физические лица должны сторониться вложений в корпоративные облигации. На то есть два простых основания:
- Риск дефолта
- Риск ликвидности
Но обычно, этих простых оснований недостаточно, чтобы убедить людей держаться подальше от «корпоратов». И чтобы показать, почему я решительно против, представляю вашему вниманию настоящую небольшую статью.
Начнём с основ. Из общего курса по инвестициям, мы знаем, что цена любой облигации определяется из простой формулы дисконтированных (приведённых) денежных потоков. При этом мы можем считать как стоимость облигации из нее, так и доходность к погашению (ставку дисконтирования) если нам известна цена на рынке. Формула 1:
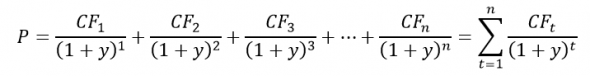
( Читать дальше )
Как я за 2 года сделал финансовый сайт в 2 раза больше Смартлаба и [почти] ничего не заработал
- 27 октября 2018, 09:10
- |
Могу кратенько спалить немного инфы о своем основном текущем интернет-проекте и заработке с него. Трейдерам будет полезно (все равно торчишь у монитора, сливаешь, хоть бы что полезное сделал). Стебусь, конечно. Ну а если серьезно, сайты позволяют серьезно диверсифицировать доходы и снизить личные финансовые риски в рамках трейдерского лайфстайла (кровать-монитор-кровать — вы же не про Майами, тачки и телок сейчас подумали?)
Как заработать на своем сайте
Начну с вводной для тех, кто в танке. В интернете есть миллионы и миллионы сайтов. Глобально они делятся на 2 типа. Половина из них что-то продает, половина ничего не продает. Те, которые ничего не продают, называются
( Читать дальше )
Обещанный Манн-Уитни
- 17 октября 2018, 13:21
- |
smart-lab.ru/blog/499678.php#comment8969912
Исходные данные: закрытия дня с 07.12.2005 по 16.10.2018 для S&P500 и индекса Мосбиржи
VAR00003, если VAR00004=0: центрированные и нормированные приращения логарифмов индекса Мосбиржи
VAR00003, если VAR00004=1: центрированные и нормированные приращения логарифмов индекса S&P500
Результат
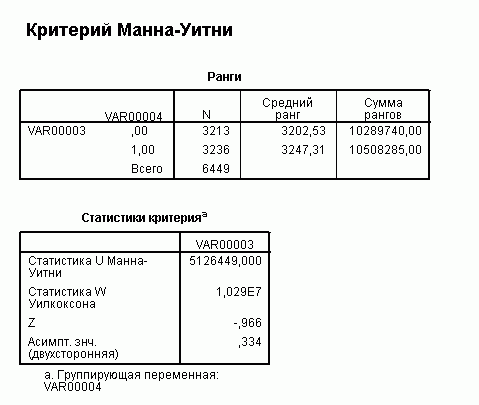
Итого: вероятность ошибиться, утверждая, что эти распределения разные, больше 0,334.
И вывод: выборочные распределения приращений логарифмов дневных значений индексов Мосбиржи и S&P500, вероятней всего, совпадают с точностью до среднего и дисперсии.
О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)
- 16 октября 2018, 16:41
- |
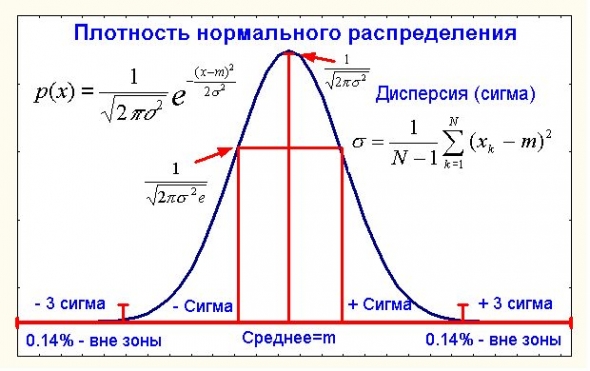
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам. Что такое центральная предельная теорема в ее классическом виде?
Пусть нам дана некоторая сумма большого числа случайных величин Х=х1+…+хN где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.
Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если xi – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x
( Читать дальше )
41 самый полезный инвестиционный пост смартлаба.
- 24 июня 2018, 14:48
- |

Тимофей запилил пост "Самые полезные посты смартлаба". Поскольку мне интересна только инвестиционная тематика то я сделал подборку самых полезных постов лучших инвестиционных авторов ресурса. В список вошли посты Малышка, Шадрина, Ларисы Морозовой, Горчакова и мои. В рейтинг вошли посты, набравшие не менее 50 добавлений в избранное (например, за последние 7 дней столько набрал лишь один пост на смартлабе). Ну хватит предисловий, ловите мой ответ Чемберлену Тимофею:
1. Александр Здрогов "Начинаю выкладывать курс по фин. анализу". Отличное начало для желающих понимать финансовую отчетность. Без этого инвестором не стать. 146 раз в избранном.
2. Александр Шадрин "Проект Разумный инвестор. Россия — страна возможностей". Огромный пост Шадрина о его фундаментальной системе (на самом деле система Бенджамина Грэма) и результатах ее тестирования. Спойлер: результаты отличные. 136 раз в избранном.
( Читать дальше )
- комментировать
- 25.3К |
- Комментарии ( 19 )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
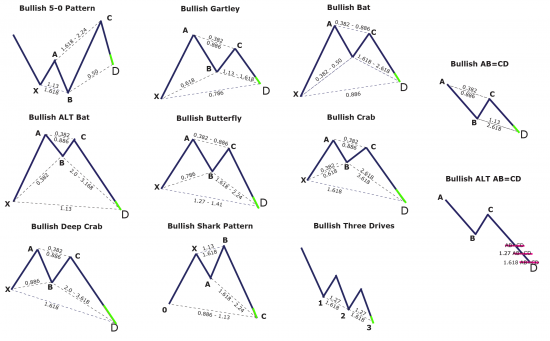
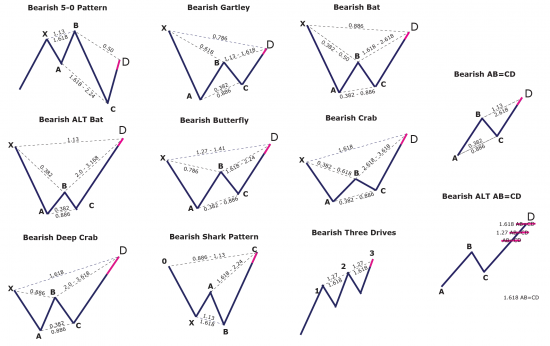
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- экономика россии
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал