Избранное трейдера ch5oh
Нефть BRENT. "За полчаса до атаки - 2". ОПЕК. Окончание игры?..
- 07 декабря 2018, 17:55
- |
Логическое окончание (?) моих статей:
Опционы и комунизьм.
Нефть BRENT. «За полчаса до атаки — 2». ОПЕК. Продолжение?..
Сегодня я лаконичен — без амуров и соплей.
Краткое содержание тех моих опусов — я продал слишком высокую, на мой скромный, волатильность (52-55). В виде стреддла на почти центральном страйке 60. И ожидал её ЗНАЧИТЕЛЬНОГО падения после «аргентины+опек».
Ну вот, собственно, и всё...
Рычночная вола ошкурена. Сдулась. Примерно на десять процентных пунктов, как я и хотел. Удержание позиции — ровно неделя (с прошлой пятницы).
Немного подпиливал дельту фьючами. Но, похоже, только немного навредил себе. Тем не менее, профиль профитов/лосей приведён ниже:
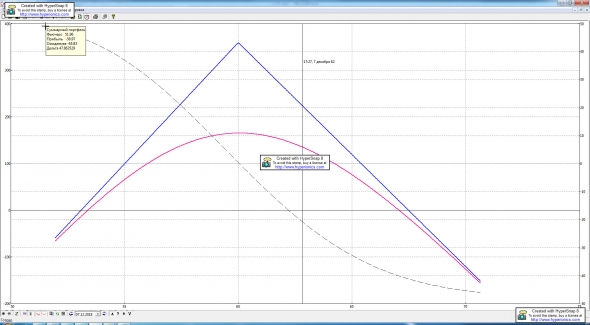
( Читать дальше )
- комментировать
- 4.1К | ★4
- Комментарии ( 29 )
Мощные индикаторы для внутридневного трейдинга на бирже. Бесплатно
- 07 декабря 2018, 11:58
- |
( Читать дальше )
Покупка баксов на бирже и вывод через вклад!
- 07 декабря 2018, 09:17
- |
Недавно снял видео где поэтапно показал как можно купить валюту на бирже, а затем вывести ее себе на счет, схему показал с целью экономии для тех кто покупает валюту в обменниках!
У многих на тот момент возник вопрос: «как я собираюсь эти деньги из банка забирать и сколько еще за это заплачу!»
Сегодняшним постом отвечаю, забрал 1000 долларов купленную по той схеме без каких-либо комиссионных или «удержаний» этих денег на счете!

Для этого посетил с паспортом ближайший Сбербанк! Комиссия за саму сделку составила 225 рублей, итоговая выгода 1 000 рублей за 1000 долларов(по обменному курсу Сбербанка на день покупки), если брать больше, выгода тоже больше!
Напоминаю в текстом виде простую схему покупки валюты:
1. Заходим в свой сбербанк онлайн, если у вас есть счет в Сбере, если нет идем и открываем любой самый дешевый карточный счет и сразу подключаем себе сбербанк онлайн(далее СО) через банкомат, на всё это у вас уйдет 30 минут!
( Читать дальше )
- комментировать
- 17.4К |
- Комментарии ( 77 )
иГРЫрАЗУМа2018.12
- 07 декабря 2018, 07:38
- |
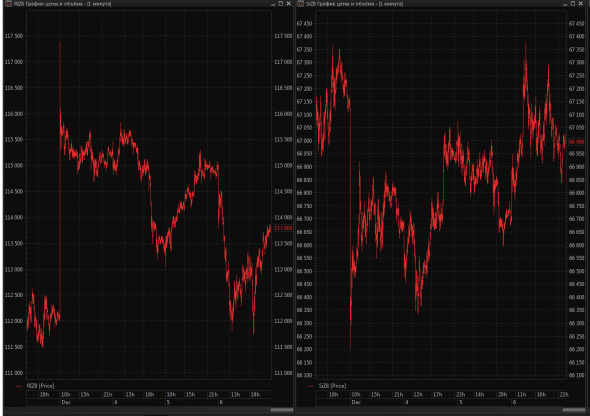
Говорят, что некоторые видят рынок на сто шагов вперед с точностью до пары шагов цены. Мы не из таких. Мы упорны в своём упорстве:
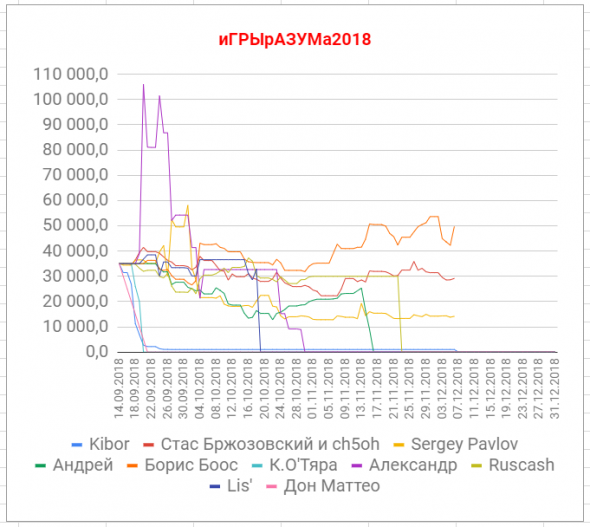
( Читать дальше )
Лучшие бумаги недели. Выпуск 2 – обновления для четверга
- 06 декабря 2018, 07:46
- |
Лучшие бумаги недели. Выпуск 2 – обновления для четверга
В таблице 1 приведены 32 наиболее ликвидные акции нашего рынка, упорядоченные по убыванию доходности за неделю с 28.11.2018 по 05.12.2018. Первые 8 акций – это лучшие бумаги недели по состоянию на утро 06.12.2018.
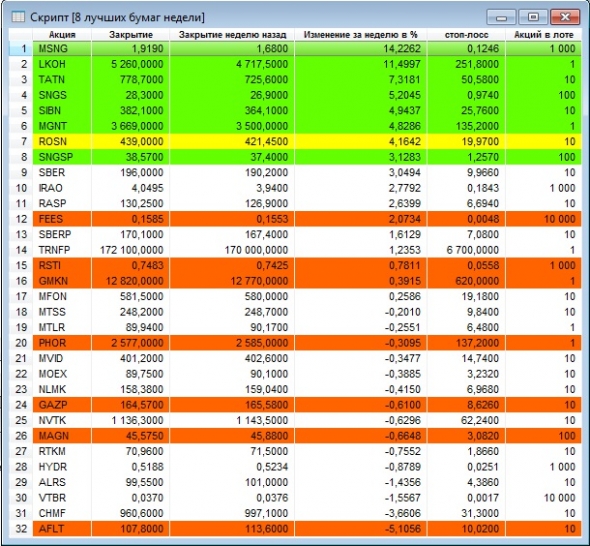
Таблица 1.
Бумаги в таблице 1 выделены тремя цветами:
- Красным - были лучшими неделю назад, а сейчас нет.
- Желтым - были лучшими неделю назад и остались лучшими.
- Зеленым — не были лучшими неделю назад, а сейчас стали.
Если вы уже торговали по этой системе, в вашем портфеле будут желтые и красные акции. Соответственно, текущая рекомендация для тех, кто обновляет свой портфель по четвергам:
- Если вы уже торговали по этой системе: продать красные акции (если они еще не были проданы по стоп-лоссу) и купить зеленые.
- Если вы еще не торговали по этой системе, купить первые 8 бумаг из таблицы 1.
- Для каждой из акций в портфеле задать стоп-лосс = цена покупки – значение стоп-лосса из таблицы 1 для соответствующей бумаги.
( Читать дальше )
Нефть BRENT. "За полчаса до атаки - 2". ОПЕК. Продолжение?..
- 05 декабря 2018, 12:27
- |
Дорогие мои Друзья. Опционщики и не только.
Как выясняется, история-то ходит по кругу. Нет-нет, да и заглянет в наш мирок, мирок торговцев фьючерсами и/или опционами нефти. С некоторой периодичностью заглядывает.
Завтра-послезавтра – сходняк ОПЕК. Стрела забита. Будет разбор, будут тёрки тереть… Сокращать – не сокращать. А если сокращать, то насколько. И комментарии, комментарии на прессухе. И видеотрансляция выступлений членов всяких. Членов ОПЕК, разумеется, а то и просто членов, фамилии не называю. (По глазам же видно, кто нагло врёт, а кто просто искренне ошибается… — прим. Автора)
А к чему это я? Ровно два года назад, 30 ноября 2016 года, состоялся очередной внеочередной, но крайне занимательный саммит этой поганенько-жуликоватенькой ОПЕК. На котором было принято историческое решение не допускать дальнейшего развала прибылей Королей и иных нефтеолигархов, а сократить квоты.
( Читать дальше )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Вопросы 3,4.
- 04 декабря 2018, 16:30
- |
3. Оправдано ли использование логарифмического нормального распределения для описания терминального состояния базового актива
Можно догадаться, почему именно логнормальную модель распределения использовали Блэк и Шолес при решении задачи о нахождении справедливой стоимости опциона. Модель с гауссовыми приращениями брать было нельзя – она допускает уход цены БА в отрицательную область. Следующая, относительно простая логнормальная модель вполне годилась. Найденное на ее основе решение стало основой всей современной теории опционов.
Теперь ложка дегтя.
Мы предполагаем, что приращения цен акций, входящих в расчет индекса РТС, независимы и подчинены закону логарифмического нормального распределения. Поэтому при вычислении цен опционов на эти акции мы используем формулы БШ.
Но, согласно Центральной предельной теореме, из этого же предположения следует и то, что распределение приращений их линейной комбинации (то есть самого индекса РТС) должно быть близким к нормальному, тогда для расчета стоимости опционов на индекс РТС правильнее использовать формулу Башелье. Тем не менее, мы используем формулу БШ. Видимо, в расчете на то, что кривая волатильности все исправит.
( Читать дальше )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Второй вопрос.
- 04 декабря 2018, 16:11
- |
- 1. Что такое кривая волатильности и как она соотносится с моделью БШ
Все знают, что такое ожидаемая волатильность опциона (Implied Volatility). Это волатильность, которую нужно подставить в формулу Блэка-Шолеса, чтобы получить текущую рыночную стоимость опциона. Вычислив ее для всех страйков, можно затем аппроксимировать полученные значения гладкой параметрической кривой – кривой волатильности.
Но, если при расчете кривой волатильности мы всегда и везде используем формулу БШ, то мы так же всегда и везде должны доверять ее авторам, а они утверждали, что волатильность опционов должна в точности равняться волатильности базового актива, которая может быть только одна. Откуда взялась кривая? Либо мы верим Блэку и Шолесу (должна быть прямая), либо не верим (тогда кривая).
У кривой волатильности нет содержательного смысла. Это простая подгонка. Единственным ее назначением является устранение расхождений между теоретическими и рыночными ценами. Какую бы модель ценообразования опционов мы ни взяли, кривая волатильности исправит все ее огрехи. Что-то вроде толстого слоя штукатурки, с помощью которого можно выровнять любую стену.
При этом мы полностью лишены возможности отличить хорошую модель от плохой, после использования кривой расчетные цены любой модели будут близки к рыночным. Тогда почему мы пользуемся именно моделью БШ? Видимо, потому, что де-факто она признана стандартной.
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Первый вопрос.
- 04 декабря 2018, 15:55
- |
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов.
В теории опционов ключевую роль играет понятие теоретической или справедливой цены. Чем правильнее она рассчитана, тем выше шансы игрока на получение прибыли. Обилие математики в опционных расчетах убеждает, что именно профессиональные математики должны преуспевать в этой игре. Не ставя под сомнение последнее утверждение, сформулирую несколько вопросов, ответов на которые и сам, вообще-то, не знаю. Вопросы, тем не менее, важные. От ответов на них зависит, вправе ли мы использовать аппарат ТВиС при нахождении справедливых цен опционов.
1. Насколько оправдано использование математического ожидания при нахождении справедливой стоимости опционов
При расчете справедливой цены опциона (то есть цены, не дающей преимущества ни одной из сторон) используется соотношение:
MO[выигрыш продавца] = MO[выигрыш покупателя] = 0
Почему именно матожидание? Ответ вроде бы очевиден – потому что это самая содержательная и самая удобная из всех числовых характеристик случайной величины. Теперь рассмотрим пример.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал