Видео www.youtube.com/watch?v=iqq6hCbU0mo документ и исходники github.com/al6x/profit_hunting/tree/main/option_norm



( Читать дальше )

Нормализация страйков, чтобы для каждого периода и волатильности были одинаковые значения страйков. 


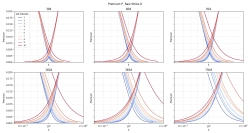
На графике:

• x нормализованные страйки K,
• y вероятность попадания опциона в ITM, в лог маштабе, CDF(K) p<0.5 и SurvivalFn(K) p>0.5 
• цвет — волатильность (дециль),
• каждая группа — это отдельный период [30, 60, 91, 182, 365, 730]. Периоды искуственно сдвинуты вверх чтобы отличить, в реальности все периоды также сливаются в одну линию.

По сути это график d2 vs F(d2).

Нормализация:

mean = log(E[S_T/S_0]) — 0.5sigma^2
d2 = (log K/S_0 — mean)/sigma

Этот же график, только каждый период на отдельном графике и в линейном маштабе.


( Читать дальше )

Формула Блак Шолес в оригинальном виде выглядит как (если принять S0=1, r = 0, T = 1, что не меняет сути):


Но в таком виде не понятно что именно она делает, ее можно переписать в визуальном виде, с понятным геометрическим смыслом



( Читать дальше )

Формула d2 нормализации страйка K


Это — z score нормализация (х-mu)/scale, где х =  ln(S/K) — страйк в лог маштабе, mu = (r-sigma^2)T локация для нормального (лог нормального) распределения на время экспирации T, и scale = sigma*sqrt(T) сигма цены на время экспирации T.

d2 нормализация говорит — какова вероятность что опцион будет в деньгах P(S>K) = F(N(0,1), d2). Таким образом сводя все опционы с любыми периодами и волатильностями, к единому маштабу. Точнее, d2 говорит не саму вероятность, а квантиль такой вероятности для N(0,1), что по сути одно и то же.

Неточности:

а) Зависит от mu — среднего, среднее чувствительно к шумам и сложно установить точно (для исторических реальных вероятностей, для IV возможно среднее устанавливается лучше).

б) Подразумевает симметричность распределения, которое в реальности асимметрично (для долгих опционов >3мес).

в) Использует нормальное распределение, которое в реальности Skew Student T.

Неудобства

Также оно имеет два неудобства

а) Вместо явного значения вероятности, которая имеет осязаемый смысл, использует ее маппинг через N(0,1) в квантиль, нечто абстрактное и неосязаемое. Одна из аргументов за — что явные вероятности имеют нелинейную шкалу а квантили более линейны.

( Читать дальше )