оптимизация портфеля

Портфельная теория Марковица

Портфельная теория Марковица(далее ПТМ) (Modern portfolio theory) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории.

Основные положения портфельной теории были сформулированы Гарри Марковицем при подготовке им докторской диссертации в 1950—1951 годах.

Рождением же портфельной теории Марковица считается опубликованная в «Финансовом журнале» в 1952 году статья «Выбор портфеля». В ней он впервые предложил математическую модель формирования оптимального портфеля и привёл методы построения портфелей при определённых условиях. Основная заслуга Марковица состояла в предложении вероятностной формализации понятий «доходность» и «риск», что позволило перевести задачу выбора оптимального портфеля на формальный математический язык. Надо отметить, что в годы создания теории Марковиц работал в RAND Corp., вместе с одним из основателей линейной и нелинейной оптимизации — Джорджем Данцигом и сам участвовал в решении указанных задач. Поэтому собственная теория, после необходимой формализации, хорошо ложилась в указанное русло.

( Читать дальше )

Акции с высокой дивидендной доходностью часто являются отличной инвестиционной стратегией для инвесторов, стремящихся получать приток денежных средств каждый год. В данной статье буден создан скрипт на Python для отбора их на бирже NASDAQ.

Что такое дивидендная доходность?

Возьму определение из Википедии. Дивиде́ндная дохо́дность (англ. dividend yield) — это отношение величины годового дивиденда на акцию к цене акции. Данная величина выражается чаще всего в процентах.

Пример

При цене акции ОАО «Лукойл» 1124,37 рублей и дивиденде 28 рублей на акцию дивидендная доходность будет равна:

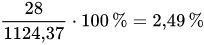
Так же необходимо обратить внимание, что многие растущие компании, такие как для примера Amazon и Yandex, не выплачивают дивиденды, поскольку они реинвестируют всю прибыль в развитие бизнеса. Поэтому дивидендная доходность для этих фирм будет равна нулю.

Расчет дивидендной доходности с помощью Python



( Читать дальше )

Вот уже как скоро 70 лет пройдет, как Гарри Марковиц явил миру математическую модель оценки инвестиционного портфеля. После того, как она завоевала популярность среди портфельных менеджеров, в 1990 он получил Нобелевскую премию за вклад в экономику. Чрезвычайная популярность модели стала возможной благодаря увеличению мощности компьютеров, позволяющих за короткое время математически обработать огромный массив данных и выдать оптимальный результат.
 
С тех пор, как любой оператор ЭВМ смог управлять инвестиционным портфелем, произошла девальвация профессии инвестиционного менеджера. Однако, прежде чем делать скоропалительные выводы, стоит убедиться на практике — является ли математическая оптимизация Граалем будущей эффективности портфеля и может быть зря в инвестиционном сообществе таких управляющих свысока именуют Квантами .

Как бы там ни было, но Марковиц смог наглядно показать, как выбор активов с наименьшей корреляцией мог существенно изменить параметры риска и доходности одного и того же по составу портфеля, в зависимости от его структуры. Согласно модели Марковица, из бесчисленного множества комбинаций можно создать портфель — единственный под инвестиционный профиль клиента, и он лежит на эффективной границе множества всех возможных портфелей.

( Читать дальше )

Начинающие (да и не только) инвесторы часто задаются вопросом о том, как отобрать для себя идеальное соотношение активов входящих в портфель. Часто (или не очень, но знаю про двух точно) у некоторых брокеров эту функцию выполняет торговый робот. Но заложенные в них алгоритмы не раскрываются.

В этом посте будет рассмотрено то, как оптимизировать портфель при помощи Python и симуляции Монте Карло. Под оптимизацией портфеля понимается такое соотношение весов, которое будет удовлетворять одному из условий:

• Портфель с минимальным уровнем риском при желаемой доходности;
• Портфель с максимальной доходностью при установленном риске;
• Портфель с максимальным значением доходности

Для расчета возьмем девять акций, которые рекомендовал торговый робот одного из брокеров на начало января 2020 года и так же он устанавливал по ним оптимальные веса в портфеле: 'ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM' и 'PKI'. Для анализа будет взяты данные по акциям за последние три года.

#Загружаем библиотеки

import pandas as pd
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt

# Получаем данные по акциям
ticker = ['ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM', 'PKI']

stock = yf.download(ticker,'2017-01-01', '2019-01-31')

( Читать дальше )

Здравствуйте, всех с наступившим Новым Годом.
По данным последних 18 месяцев был сформирован портфель акций. Характеристики:
общая стоимость 66 806 руб.; 
количество бумаг — 12 единиц (из 7 основных индексов MICEX)
доходность — 3,37% за средний расчетный месяц
риск — 2,24% за средний расчетный месяц


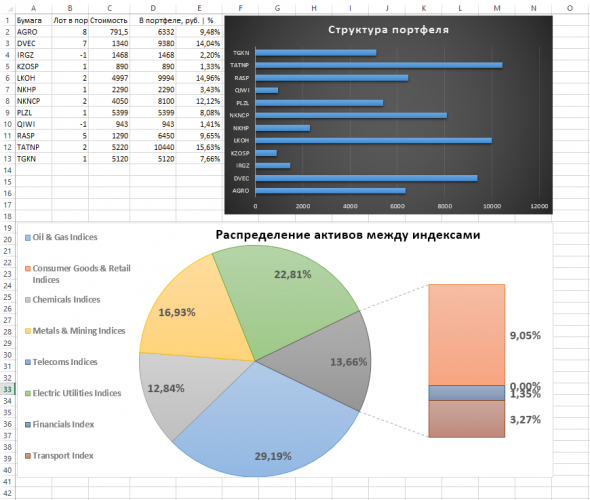
P.S. акции с отрицательным лотом в портфеле — короткая сделка.
Более детально ознакомиться с портфелем (или составить свой) можно скачав документ в группе vk - https://vk.com/family_trust. Актуальная версия на момент написания данного поста — 3.3

  
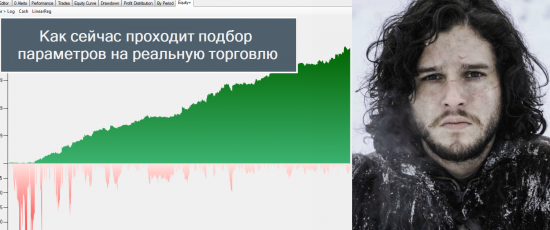
Для того, чтобы лучше понять материал, можно ознакомиться в этими статьями:
https://smart-lab.ru/blog/180975.php
https://smart-lab.ru/blog/259824.php 
Там же видео как я оптимизировал 2,5 года назад(2015 год)

+++ Спасибо за твой плюс или коммент, они важны для меня!+++
*Картинки из статьи можно смотреть тут


( Читать дальше )

Доклад «Оптимизация портфеля алгоритмических стратегий»

1. Введение

В чем состоит цель подобной оптимизации? Представим, что у нас есть набор алгоритмов, каждый из которых обладает некоторыми статистическими свойствами, из которых наиболее важными для нас являются доходность и максимальная величина просадки. В основе каждого из алгоритмов лежат разные стратегии, которые, тем не менее, могут быть коррелированы между собой в разной степени, торговля также может вестись на разных инструментах. В качестве примера приведу характеристики стратегий, которые были разработаны нашей командой и применяются в боевых торгах в настоящее время:

Так как свойства каждого из алгоритмов отличаются, возникает проблема: каким образом распределить между ними доступный капитал для того чтобы:

1. Максимизировать доход при заданном уровне риска ( то есть максимальной величине просадки)

2. Минимизировать риск при заданной доходности

Если дать, например равные доли капитала каждому алгоритму, то, очевидно, что такое распределение не будет оптимальным, так как мы не учитываем характеристики, присущие стратегиям. Не будет оптимальным и тот случай, когда мы, например, выделяем капитал пропорционально относительной доходности каждого алгоритма, здесь мы игнорируем значения волатильности, то есть риска, стратегий.

2. Модель Марковица

Задачу оптимизации попробуем решить, применив теорию оптимального портфеля, разработанную Марковицем, точнее некоторые последующие ее модификации. Обычно данная теория применяется для долгосрочного инвестиционного портфеля, состоящего из различных активов, например акций. Кратко  суть теории.

( Читать дальше )

На 25% счета я стараюсь максимизировать доходность за счет активной торговли, а на 75% — минимизировать риск. И делаю ребалансировку между ними. Во вторую часть входит портфель акций, облигации и валюта.

Так получилось, что мой портфель акций сейчас состоит из следующих эмитентов:

(«BANE», «ALRS», «TGKA», «GMKN», «RUALR», «PHOR», «AKRN», «ROSN», «OFCB»)

Причин этому несколько — требование высокой ликвидности, хорошего роста за последние годы, маленькое среднеквадратичное отклонение доходностей. Есть также диверсификация по секторам: нефть, алмазы, электрогенерация, металлы, удобрения, банк.

Поставил перед собой задачу — оптимизировать доли каждого эмитента в портфеле с целью уменьшения отклонения доходности. Увеличивать саму доходность я не ставлю целью, так как понятно, что наиболее растущих акций в таком случае будет больше всего, а история не повторится. При этом моя цель в портфельных инвестициях — сбережение. А вот минимизация риска с учетом матрицы ковариаций — это интересно.

( Читать дальше )

Для данного метода оптимизации примем некоторые допущения:

1. Доходность составляющих портфель финансовых инструментов на будущий период заведомо неизвестна.
2. Корреляции финансовых инструментов, входящих в портфель, в будущем не сильно будут отличаться от текущих.
3. Волатильности финансовых инструментов пропорциональны общей волатильности рынка, и эти пропорции не будут иметь большого отклонения от текущих значений в будущем периоде.

 

Для начала рассмотрим самый простой пример.

 Пусть у нас есть две акции  не коррелирующие между собой (их доходности и движения не зависят друг от друга).  В качестве данных для оптимизации возьмем волатильности этих акций, выраженные в виде дисперсий доходности этих акций (доходность и дисперсии рассчитаем из недельных или дневных свечей)  D1  и D2.

Необходимо определить веса акций в портфеле W1=?, W2=?  При W1+W2=1

Поскольку дисперсии D1  и D2 отражают волатильности акций, то  при отсутствии каких-либо других данных и ограничений, целесообразно  составить  портфель с весами обратно пропорциональными их дисперсий. То есть, чем больше дисперсия у акции, тем меньше ее доля в портфеле. 

( Читать дальше )