Парадокс Монти Холла

Вот вам ситуация:

1. Вы играете в игру на телепередаче. Перед вами три двери, за одной из них приз. Вам надо выбрать. Вы прислушиваетесь к интуиции и показываете на правую дверь.

2. После выбора, ведущий не трогает вашу дверь, но открывает другую, которая находится в середине. Вы видите, что приза там нет. Приз находится либо в правой двери, которую вы выбрали, либо в левой двери, которая осталась.

3. Ведущий до сих пор не открывает вашу дверь. Теперь он предлагает изменить решение — показать на левую дверь вместо правой.

4. Вопрос — что вы будете делать? Измените решение и покажете на левую дверь? Решите, что ведущий вас запутывает, и оставите первоначальный выбор? Или скажете, что шансы 50 на 50, и решение не имеет значения?


***

5. Правильный ответ — нужно менять дверь. Так вы заберете приз с вероятностью 66%.

6. Для объяснения ситуации давайте рассмотрим две стратегии игры. В обеих стратегиях мы выбираем первую дверь случайным образом. Но в первой стратегии мы никогда не соглашаемся на предложение ведущего и твердо стоим на своем. Во второй стратегии наоборот — не задумываясь меняем решение.

( Читать дальше )

Парадокс Монти Холла — одна из известных задач теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу.

Задача формулируется как описание игры, основанной на американской телеигре «Let’s Make a Deal», и названа в честь ведущего этой передачи. Наиболее распространённая формулировка этой задачи, опубликованная в 1990 году в журнале Parade Magazine, звучит следующим образом:

Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?

Наткнулся тут на замечательное доказательство высокой эффективности смены первоначального выбора.

https://www.youtube.com/watch?v=8IUGY6T0x_c

По мотивам: http://smart-lab.ru/blog/179330.php



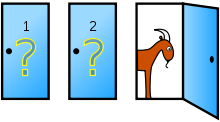
Попробую привести собственное объяснение.
 
0. Изначально вы можете выбрать или козу (К) или автомобиль (А)
 
1. Рокировка
 
1.1. Если вы выбрали — 'К', то после того как ведущий откроет дверь с 'К' и вы поменяли дверь, то это ВСЕГДА будет 'А'
1.2. Если вы выбрали — 'А', то после того как ведущий откроет дверь с 'К' и вы поменяли дверь, то это ВСЕГДА будет 'К'

Вывод: если вы меняете дверь, то вы ВСЕГДА меняете свой выбор на противоположный!!! < — Это ВАЖНО, поэтому тут делаем паузу и осмысливаем прочитанное.

Если всё понятно, идём дальше.

2. Вероятности

2.1. Вероятность того что вы изначально выберете 'К' равно 2/3 (т.к. 'К' — две штуки из выбора трёх)
2.2. Вероятность того что вы изначально выберете 'А' равно 1/3 (т.к. 'А' — одна штука из выбора трёх)

Ну тут вроде не должно возникать вопросов.


( Читать дальше )

Недавно на смартлабике внось всплыла тема парадокса Монти-Холла. В свое время я узнал о ней благодаря ЖЖ Феникса, и мне она так понравилась, что я решил ее в общем виде. Вот один частный случай, который, возможно, взворвет мозг гуманитариям:

Есть 7 дверей, за одним из которых находится автомобиль, а за 6 остальными — козы. В поисках автомобиля игрок может выбрать любые две двери, но пока не открывать их.
После выбора игрока ведущий открывает 3 из оставшихся 5 дверей, где находятся козы.
Далее игроку предлагается возможность поменять решение: вместо _двух_ дверей, которые он выбрал изначально, он может поискать автомобиль за _одной_ из других 5 дверей, из которых 3 открыты ведущим (т.е., по сути, за 1 из двух закрытых)

как выгоднее поступить игроку?


И к задаче о двух конвертах. Существует распространенное заблуждение, что обоим игрокам выгодно поменять конверты. Это неверно. Парадокс здесь на самом деле кроется в некорректном условии задачи. А именно: если считать по умолчанию распределение денег в конвертах равномерным от нуля до бесконечности, то для такого распределения не выполняется условие нормировки вероятности (мощность множества всех исходов не равна 1, а равна бесконечности). Если же взять, например, конечное равномерное распределение, или бесконечное экспоненциально убывающее распределение, то можно формально вычислить величину суммы в конверте, выше которой обмен становится невыгодным (ниже нее, соотвественно, выгодным).