Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана. 

Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на  диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами. 

( Читать дальше )

Короче нет на рынке объективности, где именно тренд а где коррекция непонять ))
Тогда я подумал всёравно ничего не понять, какая разница кто там что видит и по каким соображениям заходит, в конце концов каждый видит что хочет. Тогда я решил провести тест на истории не применяя никакой идеи, никакой системы, оставив лишь логику и исходя из того, что предвидеть не возможно и рынок это хаос.
Оставил контроль риска. Взял часовик, где вход был совершенно наобум, неважно в какую сторону, единственно что должно сохраняться, это обязательные приемлимые стопы, для меня приемлимо получилось стоп 200-300 пунктов. Далее заходим со стопом, если выбивает в следующий вход ставим такой профит который отыграет минус и даст немного профита. Цель не проигрывать сразу много а как можно дольше оставаться в игре.

Далее получилось вот что, бывает цена идёт сразу в твою сторону, но чаще против. Так вот, минусим мы значит минусим, выбирает раз за разом а часто и десять раз подряд и того, по 200-300 пунктов минус по десять раз и имеем уже 2000-3000 пунктов минус. Не всегда набирается сразу минус 2000 пунктов, но и такое бывает, особенно когда нет тренда и рынок прыгает то вверх, то вниз ) Но в итоге, сколько бы раз стоп не выбивало, рано или поздно, попадаешь на хороший движняк, который с лихвой отыгрывает минус и ещё даёт плюс. Если набралось например минус 2000 пунктов, потом попадаешь на мощный тренд который быстро отыгрывает минус и вполне даёт ёщё 1000 пунктов в плюс.

( Читать дальше )

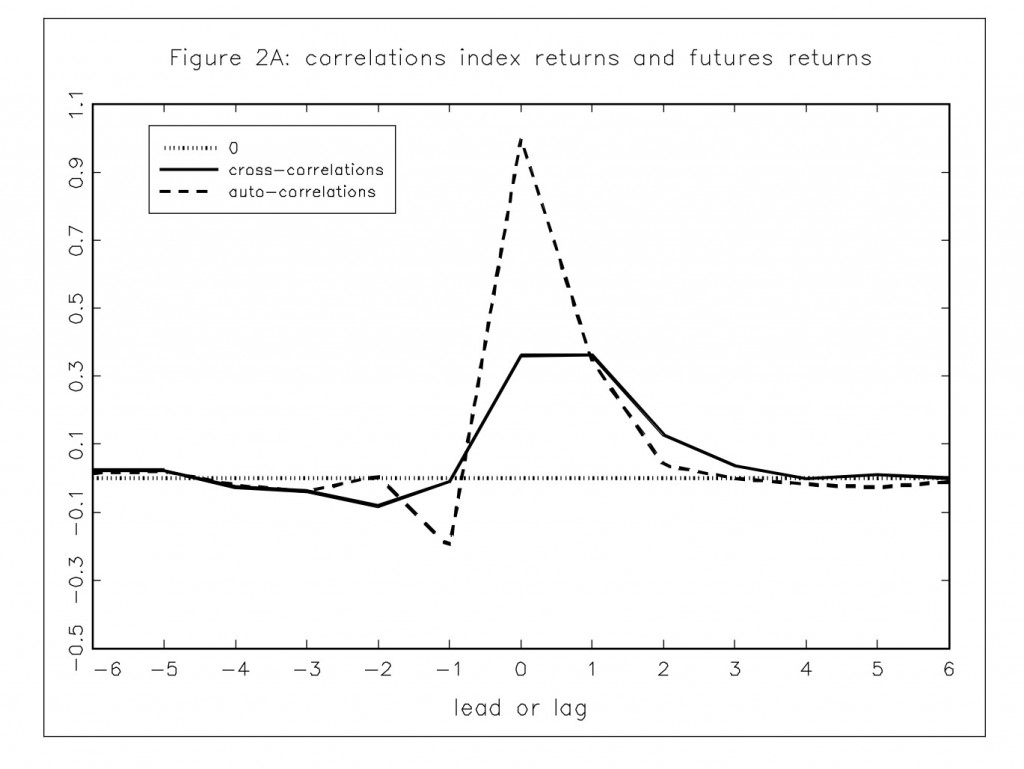
Трейдеры, которые приобрели мою программу robot_uralpro (см. пост на смарт-лабе), спрашивают, можно ли доработать алгоритм для применения его на современном рынке? Напомню, стратегия робота основана на взаимоотношении цен синтетического индекса, составляемого динамически из рыночных цен акций, входящих в индекс РТС, и фьючерса RI. Идея «одноногого» статистического арбитража, реализованного в роботе, будет работать и сейчас, только в том случае, если научиться правильно определять, какой актив опережает другой в смысле динамики их цен. Эта статья посвящена правильному выявлению такого взаимодействия, которое в англоязычных источниках называется «lead-lag relationship» -опережение-отставание между разными активами.

Те алготрейдеры, кто не приобретал robot_uralpro, тоже сочтут эту статью полезной, так как lead-lag relationship может использоваться в стратегиях парного трейдинга и им подобным. Например, определив такое взаимодействие, можно исключить из парного трейдинга один из активов ( с учетом того, конечно, что отношение торгуемых инструментов было описано четкой моделью) и значительно увеличить тем самым прибыльность стратегии.

( Читать дальше )

 

p.s. тем кто в это все верит, главное понимать, что переоптимизированные системы такие живут только пока рынок не встанет в боковик

1889 трейдов за 20 сек. 
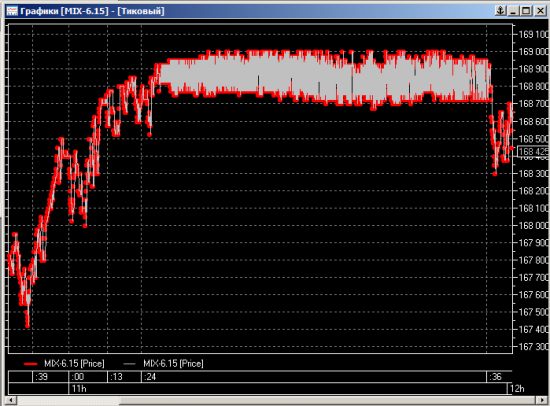
финрез ~ -2 мио 
получается ~ -100 тыр /сек
из 1889 тиков 76% имеют последовательные номера сделок
что некоторым образом информирует нас о плотности транзакционного потока 

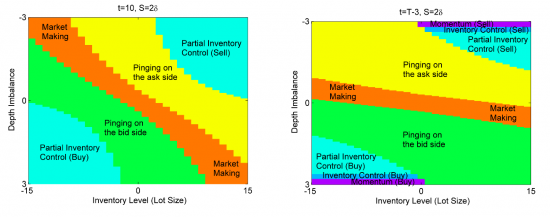
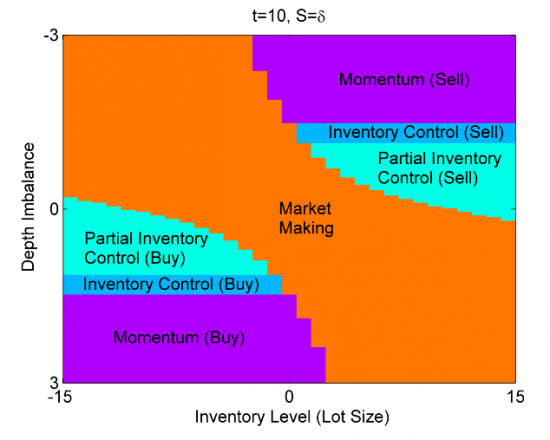
Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ,  как достижение максимума следующего матожидания:

,

( Читать дальше )

Наконец, дошли у меня руки, что я и сам купил немного долларов через Московскую биржу. Ранее на смартлабе подробнее процесс описывали, многие даже добавили эти инструкции в закладки, и вам рекомендую:

Как купить валюту на бирже? (+266,113к,35f)

Обмен валюты на бирже? (+15,5к)

Обе инструкции при помощи брокера Альфа-Директ при Альфа-Банке. Повторять я их не буду, просто хочу подтвердить, что все работает, как описал автор в первом топике. Я и сам пользуюсь Альфа-директом еще с 2008 года, не буду ничего говорить о качестве брокерского обслуживания, но надо сказать, в плане покупки валюты, похоже именно у Альфы есть преимущества перед остальными:

• Быстрый вывод долларов на долларовую карточку VISA/Mastercard (у меня где-то через 25 минут деньги появились на карте, то есть деньги шли ровно столько, сколько я писал этот пост)
• Минимальные издержки, нет левых комиссий
• Удобно вносить/снимать рубли/доллары через банкоматы альфы 

Единственный недостаток — это долгая бюрократизированная процедура открытия счета. Но это всего один раз. Какие нюансы я бы отметил:

• Если выводишь деньги сразу после покупки их на бирже, удерживается какая-то плата на счете. Поэтому выводить лучше на следующий день
• Заявки кратны только $1000. Меньше обменять не получится.

Говорят, что в «Открытии», например, проблема — снять налик в кассе, и там берут большой комисс в % от счета, при снятии долларов. У Альфы такого нет, сколько купил — столько и вывел.

Если совсем коротко, то процедура выглядит так:

1. вносишь рубли в банкомате на счет
2. в интернет-банке (альфа-клик) переводишь их на брокерский счет
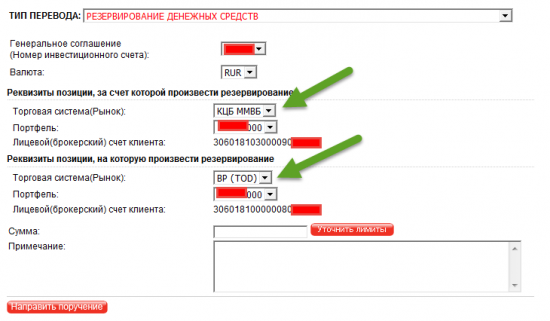
3. в альфа-директе переводишь их на ВР МБ (валютный рынок)
4. кстати только что узнал, что можно сразу в интернет-банке перевести с банковского счета на МБ ВР, то есть объединив пункты 2 и 3
5. далее в альфа-директе надо ткнуть в таблицу «котировки» выбрать инструменты — доллар-сегодня (TOD) и доллар-завтра (TOM)  
6. тыкаем в USD(TOD), лично я покупал через ТОД т.к. тут доллар на несколько копеек дешевле и отгружается на день раньше:) Правда купить на ТОДе можно только до трех часов вроде
7. то что валюта приобрелась, можно убедиться, посмотрев в табличку «балансы», строка валютный.
8. выводим так же, как вводили, можно даже через альфа-клик

пункт 3:
 


( Читать дальше )

В прошлой части мы рассмотрели оптимальное управление inventory risk в маркетмейкерском алгоритме. Напомню, что формулы для нейтральной цены и оптимального спреда между лимитными ордерами были получены при допущении, что цена следует геометрическому броуновскому движению. Управление inventory risk для моделей цены, более приближенными к реальности, рассматривается, например, в статье Pietro Fodra & Mauricio Labadie «High-frequency market-making with inventory constraints and directional bets» . Однако, применить напрямую на практике алгоритмы из этих статей вряд ли получится, так как в них  не учитывается действие adverse selection risk. Поэтому в данной части рассмотрим работу JIANGMIN XU «Optimal Strategies of High Frequency Traders», в которой автор делает попытку учесть этот вид риска, конечно, наряду с inventory risk.

( Читать дальше )

Выпадает синий экран при запуске квика )

 

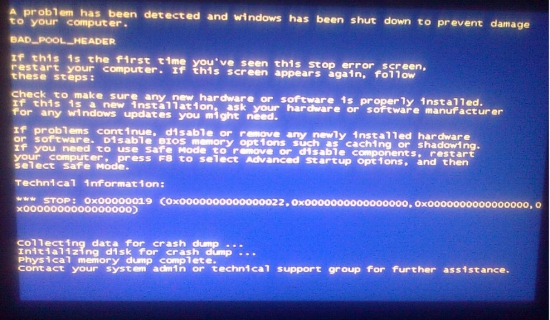
Не знаю короче что за фигня ) Уже всё перпробовал ) Комп работает норм, но квик не работает ) Квик сбера, соединение через ФПСУ клиент.
Я уже всё удалил и квик и клиент, скачал заново с сайта сбера. Сам ФПСУ соединяется норм, но когда открываеш квик и он начинает получать данные, выпадает синий экран ) Я уже в поддержку квика написал, говорят это ошибка ФПСУ клиента, он является продуктом фирмы АМИКОН ) Короче я уй знает что делать ))) Позвоню брокеру, но если разрабы не знают в чом причина, то не знаю )) По данной ошибке в нете ничего конкретного не нашёл )

P.S.: проблема решена ) Скачал драйвер с сайта амикон для хуавэй 3G модема, работает как часы, всем спасибо и спасибо тех.поддержке брокера, который ответил не глядя за дну секунду ) вот где спецы )