Блог им. AGorchakov |Опционы, они такие
- 28 апреля 2023, 17:33
- |
Банк России во взаимодействии с профессиональным участником рынка ценных бумаг (далее — Брокер) установил факты манипулирования рынком ряда опционов на организованных торгах в период с 01.11.2019 по 03.12.2021 сотрудником Брокера Кривошеевым Константином Евгеньевичем.
Полностью тут
Мой комментарий. Не удивлен, в пустых «стаканах» наших опционов можно и не такое «творить». Я вообще не понимаю, что можно там считать при нынешних спредах в премиях на нормальный сайз. Ясно, что кто-то рано или поздно должен был этим воспользоваться. Кстати, это относится не только к опционам, а к любым инструментам со спредами в «стаканах» на нормальный сайз от 10%+. Вообще на месте ЦБ я бы начал мониторить инструменты на предмет «наполненности стаканов» и на основе четкого критерия «наполненности стакана» разделить инструменты на «для всех» и «только для квалифицированных инвесторов».
- комментировать
- ★3
- Комментарии ( 71 )
Блог им. AGorchakov |О ценах, модели Блэка-Шоулза и графическом анализе. Часть 1
- 30 января 2023, 13:06
- |
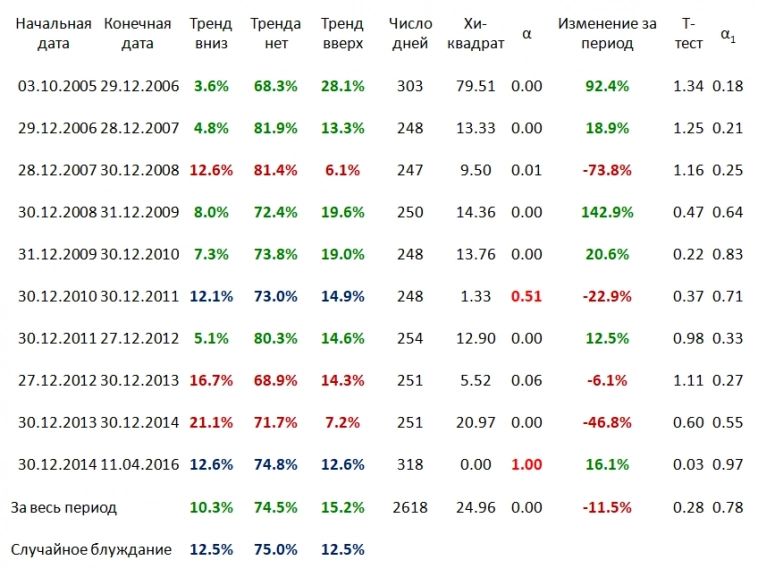
Эту таблицу я впервые приводил в своем выступлении на конференции Смартлаба весной 2016-го и повторил на конференции 2018-го, акцентировав внимание на том, что хочу оформить письменно ниже
Что в таблице? В таблице доли участков RI (фьючерс на индекс РТС — прим. мое) из 10 приращений, как по отдельным периодам, так и в целом, которые я отнес к «трендам». Что я считал «трендом»? «Трендом» я считал участки, на которых среднее приращений цен (или приращений логарифмов цен, что эквивалентно) отлично от нуля и если оно больше нуля, то относим отрезок к «трендам вверх», а если меньше нуля – к «трендам вниз».
Какой использовался критерий? Обычный модифицированный критерий Стьюдента на отличие приращений логарифма(!) цены от приращений гауссовского процесса со средним нуль и дисперсией «почти равной» для 9 испытаний из 10 (нулевая гипотеза). Так как мы имеем критерий на различие сложной гипотезы против простой, то распределение статистики критерия точно известно нам только при простой гипотезе. И потому при априори выбранных границах критерия мы можем знать только вероятности попадания последовательности из 10 значений в наши «классы» при верности нулевой гипотезы.
( Читать дальше )
Блог им. AGorchakov |Карлсону: вот кого надо заманить в игры разума
- 12 октября 2021, 18:06
- |
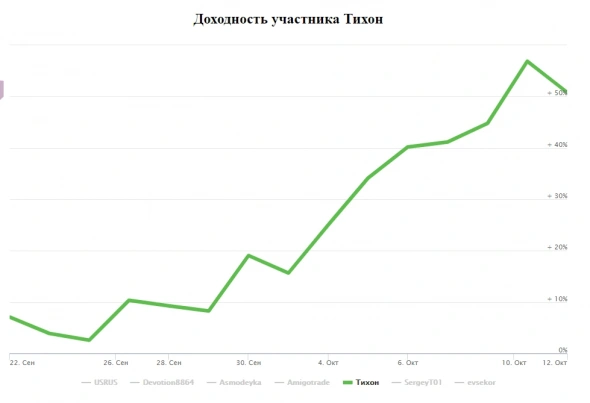
investor.moex.com/trader2021?user=292012
Я с его опционной позой разобраться не смог, но эквити впечатляет.
Блог им. AGorchakov |Об "ухмылке" волатильности
- 07 мая 2021, 10:39
- |
Даже цитируются «умные» книги о том, что спрос на путы больше из-за наличия хэджеров.
На самом деле все проще и иначе.
Вот общее определение «справедливой» цены произвольного платежного поручения
Итак, пара общих определений.
Платежное поручение — это обязательство продавца выплатить некоторую сумму покупателю, зависящую от цены базового актива в будущий момент времени Т — С(Т).
Платежной функцией платежного поручения называется функция выплат f(C(T)).
Тогда справедливой ценой платежного поручения можно считать среднее f(C(T)) по распределению будущей цены С(Т) (чаще всего неизвестному точно), деленную на 1+R, где R- безрисковая ставка до момента времени Т.
( Читать дальше )
Блог им. AGorchakov |Ох, и навел я "тень на плетень" в прошлом топике про "безарбитражность"
- 22 февраля 2020, 12:54
- |
N+C-S*(1+R)-1
из которых С мы должны отдать на покупку актива, остается
N-S*(1+R)-1.
Если эта величина отрицательна, то мы должны на нее прокредитоваться под безрисковую ставку, если положительна, то разместить под безрисковую ставку. Что мы имеем? Мы имеем либо кредит, либо депозит плюс позиция, которая гарантировано нам даст выплату в размере S на экспирацию. Почему верно последнее? Очень просто. Если цены упадут, то проданный колл «сгорит», а купленный пут мы реализуем и получим S, если цены вырастут, то купленный пут нам не нужен, а по проданному коллу мы продадим актив за S. Получается, что кредит нам принесет только убыток и потому он бессмысленен и конструкция имеет смысл только при N>S*(1+R)-1. Последнее неравенство можно спокойно заменить на равенство, так как задействовать капитал под эту конструкцию больше S*(1+R)
( Читать дальше )
Блог им. AGorchakov |«Безарбитражность» - «афера века»
- 21 февраля 2020, 11:05
- |
В обсуждении прошлого топика совместно с коллегами мы пришли к выводу, что необходимым и достаточным условием безарбитражности в опционах европейского типа является колл-пут паритет
Call-Put=C-S*(1+R)-1
где
Call – цена опциона колл со страйком S;
Put – цена опциона пут со страйком S;
С – текущая цена базового актива (БА, предполагается, что в активе нет купонов и дивидендов);
Собственно, рассуждения в рамках безарбитражности приводят нас к условию, что среднее относительного приращения цены БА до экспирации равно R.
А что получается при колл-пут паритете, когда то же самое среднее в 20 и более раз больше R?
Сразу сделаем предположение, как у Блэка-Шоулза, что мы всегда можем занять любую сумму под ставку R.
Рассмотрим для простоты актив, который на любую будущую экспирацию имеет два равновероятных исхода: +30% и -10%, а R положим равным 1%.
Для простоты также будем считать, что 0.99*1.01=1, т. е. все в расчетах будем округлять до 0,1%.
( Читать дальше )
Блог им. AGorchakov |Опционы? Да легко
- 28 ноября 2019, 21:44
- |
Вот тут давно описана моя система продажи путового месячного «края» и приведены ее тесты с 2008 по 2013:
www.howtotrade.ru/nw/index.php?p=1380184332
Вскоре после той публикации эта система начала торговаться в реале на объеме в почти 1000 контрактов в сумме (на фирме 960 контрактов). 3 марта 2014 торговля этой системы была закрыта. Почему? Ссылку на это дам в конце (я уже об этом тут писал), потому что это будет хорошим резюме к нижеизложенному.
Собственно расчет вариационной маржи для 960 контрактов я продолжил и после прекращения торговли. Эдакий out-of-sample. И что получается? А вот что по дням экспирации (мы помним, что продаваемые опционы месячные)
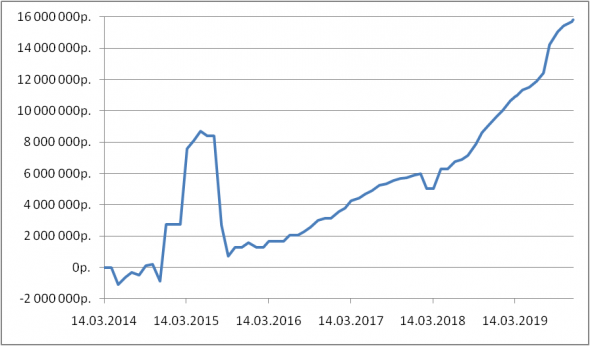
График в рублях, потому что я не знаю к чему отнести накопленную вармаржу. Ну до сентября 2015-го выглядит не очень красиво, я бы такое не торговал, но с 15 сентября 2015-го очень даже симпатично
( Читать дальше )
Блог им. AGorchakov |К вопросу о непокрытой продаже опционов
- 17 апреля 2018, 16:07
- |
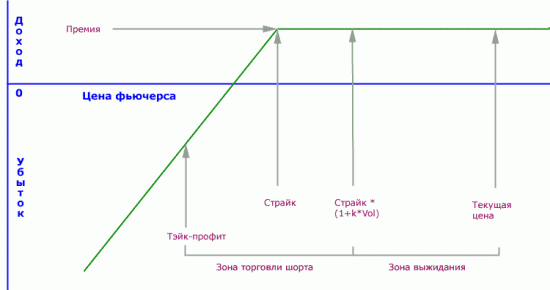
Так вот, и в пятницу 28.02.2014 (Страйк=120000) и в пятницу 06.04.2018 (Страйк=110000) система была в непокрытой продаже пута. НО! Если 3 марта рынок открылся и проскочил две (!) планки и вторая была ниже Страйка проданного опциона, то 9 апреля рынок открылся гораздо выше Страйк*, который был под первой планкой и по этой цене прекрасно бы открылся шорт, если б хватало денег под ГО (а у меня бы его точно хватило, так как пут я тогда продавал исходя из соотношения Страйк*число контрактов~депозит и сейчас бы не изменил этому правилу, а на трендовых системах на том же депозите могли быть только шорты). И что? А то, что на вчерашний вечерний клиринг эта система была бы в плюсе к 06.04 и только сегодня бы ушла в небольшой минус из-за роста на вчерашней вечерке и сегодня утром (и еще неизвестно, что будет к вечеру). А потому вывод: в этот раз непокрытые проданные путы «на краях» без плеча (т. е. когда Страйк*число контрактов~депозит) вообще не несли в себе рисков, а риск был в повышении ГО и нехватке средств из-за огромных плечей.
Блог им. AGorchakov |М-да, это даже не 3 марта 2014-го
- 06 февраля 2018, 10:33
- |
Блог им. AGorchakov |Maximum Profit System для опционов
- 23 декабря 2013, 12:01
- |
Е*max(x-d,0), где Е* –среднее по распределению P* случайной величины d.
Предположим, что безрисковая ставка равна нулю и мы имеем опционы европейского типа с их рыночными ценами Ccall(St) и Сput(St), базовый актив с ценой C0 и отсутствие возможности арбитража. Тогда из известной теоремы о безарбитражном рынке следует, что существует такое распределение (Ррын) относительного приращения будущей цены базового актива dT=CT/C0-1, CT — цена на экспирацию, что ЕрынdT=0 и для любого страйка имеют место равенства
Ccall(St)=C0·(gрын(s)- s) и Cput(St)=C0·gрын(s),
где s=St/C0-1.
Распределение Pрын еще называют «риск-нейтральным», потому что если реальное распределение dT-M
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс