теория вероятностей

Почему то видео с моей первой лекцией из курса, открываемые организаторами курсов по моей просьбе, со временем исчезают из сети. Поэтому решил разместить эту лекцию на своем канале на Ютубе.

PS. Смотреть лучше со скоростью 1,25 :)

Примерно год назад я опубликовал здесь статью, где показал результат расчета вероятности n убыточных сделок подряд.

Так, например, я показал, что серия из 9 убыточных сделок подряд возникнет хотя бы раз при совершении 1000 сделок. А серии из 4 убыточных сделок подряд будут в среднем возникать в районе 30 раз на 1000 сделок.

Сегодня у меня появилась еще одна интересная мысль после того, как я посмотрел свой торговый журнал. Ниже приведен финансовый результат 20 моих последних сделок:



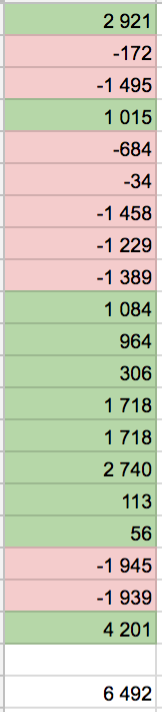
Итог — примерно 6500 рублей прибыли. 

Тут мы видим, что у меня была серия из 5 убыточных сделок подряд. Также мы видим, что затем была серия из 8 прибыльных сделок подряд. 

Так вот, основная мысль, которую я хочу сказать, в том, что теория вероятностей работает не только против нас, но и за нас. Если у вас серия из 3 убыточных сделок подряд, то значит у вас будет серия и из 3 прибыльных сделок подряд. Всегда нужно помнить об этом и это поможет вытерпеть длинные серии проигрышных сделок.

То есть тот же расчет для n убыточных сделок подряд работает и для n прибыльных сделок подряд и за 1000 сделок у нас должна быть серия из 9 прибыльных сделок подряд хотя бы 1 раз, а серий из 4 прибыльных сделок подряд будет 30 раз.

Сложился стереотип, что теория вероятностей – это человеческая наука  о случайности. На самом деле это не совсем точно. Это математическая дисциплина, изучающая свойства вероятностных пространств. Что такое вероятностное пространство? Это человеческая математическая модель для случая, когда пока ненаблюдаемое является набором событий с некоторыми шансами их появления, как минимум, два из которых ненулевые. А что такое случайность? Это когда наше лучшее знание о пока ненаблюдаемом является набором событий с некоторыми шансами их появления, как минимум, два из которых ненулевые. Т. е. теория вероятностей занимается лишь изучением второй части из определения случайности и никак не доказывает и не опровергает гипотезу о нашем лучшем знании о пока ненаблюдаемом. Т. е. в основе теории вероятности лежит гипотеза об объективном существовании случайности.

И как определяется вероятностное пространство? А определяется оно исключительно в виде частного случая теории множеств, лежащей в основе всей современной математики. Откажитесь от теории множеств и вся современная математика рассыпается в прах.

( Читать дальше )

Здравствуйте, продолжим разговор о мани менеджменте, многие слышали такую игру в монетку, подбрасываем и если мы выиграли забираем допустим 2 если проиграли отдаем 1 и многие знают что на большом участке выборки мы должны быть в плюсе, так вот хотелось бы поговорить как это воплотить на рынке, многие сразу подумают что надо торговать 1 к 2 но при правильном анализе данная концепция ошибочна, шанс что сработает стоп будет чаще что уже не соответствует 50 на 50, так что же делать как сделать так чтоб торгуя 1 к 1 (только это соотношение дает 50 на 50) сделать так что при одинаковой начальной ставки — при выигрыше было 2 а при проигрыше 1, вернемся к нашему любимому мани менеджменту и решим данную задачу простым способом)) торговать будем 1 к 1 число контрактов 2 если цена идет в нашу сторону то мы получаем выигрыш 2 а если цена идет не в наши сторону то мы убираем один контракт что приведет к потери в 1,5 контракта ))) получаем при соотношение 1 к 1 на длительном пути мы будем в плюсе ))) можете проверить на соотношение случайных чисел 0 или 1))
Успехов всех в торговле, информация просто к размышлению и выполнению поставленной задачи игры в монетку. 

Аж самому понравился мой же коммент.
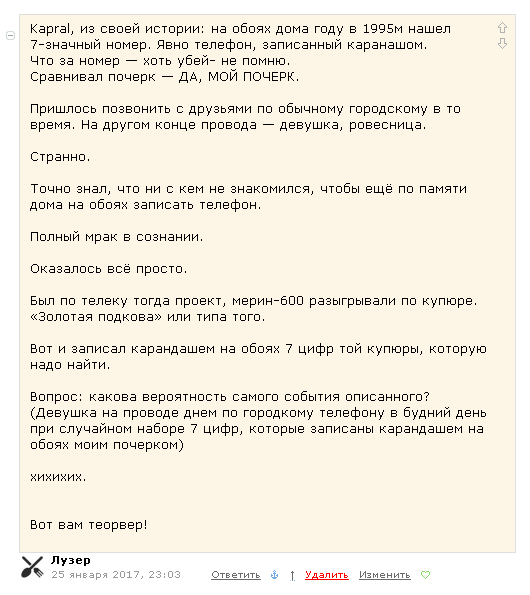
Вынесу отдельно.
(история реальная).

Спасибо smart-lab.ru/blog/376542.php

В настоящее время компьютеры могут многое. В том числе они помогают проверить, правильно ли мы рассуждаем с использованием математических методов, не закралась ли где-то ошибка. В посте Тестик. Наивный Теорвер предлагалось решить задачу про робота, который ходит по квадратному листу книги.

Большая просьба, особенно к А.Г.))), не писать сразу решение)))

Поскольку времени подумать над задачкой всем заинтересовавшимся было достаточно, пора разобраться с тем, каков же правильный ответ. Ниже приводится решение методом Монте-Карло.



( Читать дальше )

Всем привет, посмотрел и почитал посты определенных гуру рынка который решает кто прав кто не прав, работает теория вероятности не работает, можно долго спорить и разговаривать с такими личностями, но вопрос один почему все эти умники понимающие рынок такие бедные.
На этот вопрос ответа у них не будет, а не будет его потому что сами себе они не могут и уже не хотят задать вопрос что они делают не так, у них есть свое понимание чего либо и они могут кому угодно доказать свою правоту, вот только одна проблема конечный результат вашей эффективности на рынке?- это деньги!!! Я вижу у самых умных, популярных личностях, денег почему то очень мало.)))) Поэтому когда вы называете людей использующих ту или иную схему торговли на рынке тупыми или неудачниками, знайте мы знаем по чему вы так говорите, вы просто всегда хотите остаться правым во всем, нет проку от вашей точки зрение так как она не подкреплена вашим успехом на рынке. 
Думаю ни кого не обидел и дал понять не которым личностям, что перед тем как кого то оценивать, посмотреть на себя. 
пс. не написал в темах так как забанен у гуру рынков!!!

Есть 1000$ и есть игра в которой вероятность выйгрыша (удвоения ставки ) 66 % тоесть мы 2 раза выигрываем 1 раз проигрываем,
составить алгоритм с максимальной вероятностью остаться с 1 млн $, ограничение количества игр 200.

1. вариант стивам каждый раз всю сумму тогда нам нужно выйграть подрят 10 раз, итого наша вероятность выйграть 1млн (0.6)^10= 0.015 или
1.5% полтора процента.

2. варант ставим всегда половину, тогда допустим 2 первые раза мы выйграли и 1 проиграли, 100+50=150, 150 +75=225,
225-112.5 = 112.5 итого за 3 игры наш капитал увеличивается на 12.5% процентов. итого (1.125)^x=1000, x=61 ,
61*3= 183 игры через 183 игры наш капитал увеличится в 1000 раз, и если посчитать (через формулу лапласа 183 игры
вероятность того что мы выйграем 61 и более раз ( F((121-183*0.66)/( sqrt(183*066*0.33)) — F(((121-183*0.66)/( sqrt(183*066*0.33)))=
=F(1.913) = 0.94 )
с вероятностью 94 % за 183 игры мы увеличим свой капитал в 1000 раз.

3. варант ставим 2 третьи капитала, 100+66=166, 166+110=276, 276 — 184 = 91.5, Внимание! итого
2 раза выйграв и 1 раз проиграв мы остамся в убытке на 8.5%!

4. Ставим треть капитала, 100 + 33 =133, 133 + 44 = 177, 177 -59 = 118, выгоднее чем половина, 18% И 12.5% на 5.5%.

( Читать дальше )

Завершаем цикл статей Виктора Аргонова о теории вероятностей. Сегодня мы отвечаем на извечный вопрос: можно ли купить счастье?

( Читать дальше )

В рамках цикла статей Виктора Аргонова о теории вероятностей сегодня мы расскажем о задаче, которая не имеет прямого отношения к задаче о случайном блуждании, но которая не менее парадоксальна и “крышесрывна”. Это вновь задача об азартной игре, а именно — о лотерее.

( Читать дальше )