SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
парадокс
Операции по парадоксах
- 21 января 2016, 16:44
- |
Позиции, открытые по принципу парадокса в разнице между заявками и свечами. Это немножко другой принцип, чем я описывал в посте smart-lab.ru/blog/304459.php, но на основе той же идеи парадокса рынка.
Скажу сразу, что последняя операция себя не отработала
Скажу сразу, что последняя операция себя не отработала

- комментировать
- 17 | ★1
- Комментарии ( 2 )
Парадокс...
- 08 июня 2015, 20:33
- |
Парадокс времени ожидания.
Предположим, на некоторой установке указан интервал движения автобусов 10 минут. Тогда естественно считать, что люди ждут автобус в среднем 5 минут. Однако оказывается, что среднее время ожидания может не только превысить 5 минут, но и быть бесконечным!
Примечание. Если m — математическое ожидание, s — отклонение, то среднее время ожидания Т=( m2+ s2)/(2*m) и Т= m /2 только при s =0. Обычно же m=s и автобуса приходится ждать 10 минут.
Парадокс смертности.
Эдмунд Галлей (открывший известную комету) в 1693 году составил таблицу смертности, положившую начало математической теории страхования жизни. По этой таблице средняя продолжительность жизни равна 26 годам, и вместе с тем с равными шансами можно умереть до 8 лет и прожить больше 8 лет. Как это увязать?
Парадокс независимости.
Предположим, что бросают две правильные монеты. Пусть событие А — «на первой монете выпал герб», событие В — «на второй монете выпал герб» и событие С — «на одной (и только на одной) монете выпал герб». Тогда события А, В и С попарно независимы, но любые два из них однозначно определяют третье.
( Читать дальше )
Предположим, на некоторой установке указан интервал движения автобусов 10 минут. Тогда естественно считать, что люди ждут автобус в среднем 5 минут. Однако оказывается, что среднее время ожидания может не только превысить 5 минут, но и быть бесконечным!
Примечание. Если m — математическое ожидание, s — отклонение, то среднее время ожидания Т=( m2+ s2)/(2*m) и Т= m /2 только при s =0. Обычно же m=s и автобуса приходится ждать 10 минут.
Парадокс смертности.
Эдмунд Галлей (открывший известную комету) в 1693 году составил таблицу смертности, положившую начало математической теории страхования жизни. По этой таблице средняя продолжительность жизни равна 26 годам, и вместе с тем с равными шансами можно умереть до 8 лет и прожить больше 8 лет. Как это увязать?
Парадокс независимости.
Предположим, что бросают две правильные монеты. Пусть событие А — «на первой монете выпал герб», событие В — «на второй монете выпал герб» и событие С — «на одной (и только на одной) монете выпал герб». Тогда события А, В и С попарно независимы, но любые два из них однозначно определяют третье.
( Читать дальше )
Перекос вероятности в оценочном суждении
- 08 мая 2015, 11:43
- |
Прикол в том, что я на 100% уверен, что индекс РТС когда-нибудь будет 1200 п. и 2000 п. тоже, но я совсем не уверен, что он когда-нибудь будет 600 п.
Степаном Д. "Золото и Центральный Банк РФ"
- 26 июня 2013, 09:40
- |
Очередной неплохой эфир со Степаном Д. (гость у него интересный -Валентин К.)
Золото и Центральный Банк РФ
Золото и Центральный Банк РФ
Вопрос дня! Парадокс?
- 24 апреля 2013, 10:46
- |
Роснефть добывает больше нефти чем Exxon Mobil
Зато выручка Exxon больше в 3 раза, а прибыль — в 4 раза:)
Парадокс?
-------
Вчера был день инвестора Роснефти. Впервые были озвучены результаты объдиненной компании. и выглядят они весьма прилично.
выручка $160Б
ЕБИТДА $33,4Б
Прибыль $16,7Б
Чистый долг $66,8Б
Капитализация Роснефти $72Б
Лукойл
выручка $139Б
ЕБИТДА $18,9Б
чистая прибыль $11Б
чистый долг $3.7Б
Exxon
Выручка $467млрд (офигеть!)
Чистая прибыль $45B
Сделал вот такую табличку
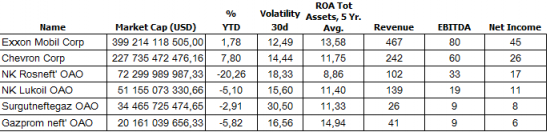
Зато выручка Exxon больше в 3 раза, а прибыль — в 4 раза:)
Парадокс?
-------
Вчера был день инвестора Роснефти. Впервые были озвучены результаты объдиненной компании. и выглядят они весьма прилично.
выручка $160Б
ЕБИТДА $33,4Б
Прибыль $16,7Б
Чистый долг $66,8Б
Капитализация Роснефти $72Б
Лукойл
выручка $139Б
ЕБИТДА $18,9Б
чистая прибыль $11Б
чистый долг $3.7Б
Exxon
Выручка $467млрд (офигеть!)
Чистая прибыль $45B
Сделал вот такую табличку

Заработок на бреднях - парадокс трейдинга
- 24 февраля 2013, 22:31
- |
Щас идет оживленное обсуждение персоны Майтрейда и я как то вспомнил многих знаменитых трейдеров которые заработали состояние и славу на… бреднях!
Например знаменитый Алигатор Вильямса — когда я впервые прочел о нем, то был шокирован — че за бред? Человек на полном серьезе описывает как крокодил пасть открывает, как закрывает и т.д.
далее вспомнились уровни Фиббоначи какие то мистические (прям мировой код тайный :))), волны Эллиота (5 волн должно быть полюбому :))), волны Вульфа с бабочками (бабочка крылышками бяк-бяк-бяк, а ее воробушек шмяк-шмяк-шмяк :)), экраны Элдера с колокольчиками и т.д. и т.п. — особенно популярны разнообразные теории заговоров :)
то есть люди описывали свое видение поведения цены не с точки зрения рыночных реалий, а просто каких то выдумок, которые к тому же не имеют никакого отношения к рынку.
-----------------
И вот тут подумалось — а ведь любая теория, какой бы ошибочной она не казалась, если сможет описывать ТЕКУЩЕЕ состояние рынка, то по ней можно зарабатывать!
( Читать дальше )
Например знаменитый Алигатор Вильямса — когда я впервые прочел о нем, то был шокирован — че за бред? Человек на полном серьезе описывает как крокодил пасть открывает, как закрывает и т.д.
далее вспомнились уровни Фиббоначи какие то мистические (прям мировой код тайный :))), волны Эллиота (5 волн должно быть полюбому :))), волны Вульфа с бабочками (бабочка крылышками бяк-бяк-бяк, а ее воробушек шмяк-шмяк-шмяк :)), экраны Элдера с колокольчиками и т.д. и т.п. — особенно популярны разнообразные теории заговоров :)
то есть люди описывали свое видение поведения цены не с точки зрения рыночных реалий, а просто каких то выдумок, которые к тому же не имеют никакого отношения к рынку.
-----------------
И вот тут подумалось — а ведь любая теория, какой бы ошибочной она не казалась, если сможет описывать ТЕКУЩЕЕ состояние рынка, то по ней можно зарабатывать!
( Читать дальше )
Парадокс со Степаном Демурой
- 11 января 2013, 21:39
- |
все-таки я даже рад, что в жизни Степана случились изменения. Потому что его соло теперь можно слушать и не отвлекаться ни на каких типов, а новый формат поможет Степану полностью высказаться и самореализоваться.
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
