алгоритм

Торгуй алгоритм! Разоблачение...

У новичков бытует мнение, что нужно придерживаться своего торгового алгоритма, соблюдать правила и вот тогда уж точно будет профит.

Это мнение навязывается всякими околорыночными гурами. Они говорят:

— Вот тут ты не обрезал убыток, а тут не дал прибыли течь…у тебя проблемы с контролем эмоций… (Задним числом я тоже могу быть таким гуру )

На этом построен огромный околорыночный бизнес по обучении психологии, теханализ, самоконтроль и т.д.

Сливающим новичкам кажется, что у них проблема в психологии, что они не могут строго придерживаться правил своей системы и поэтому они сливают. Но так ли это на самом деле? Давайте разберемся.

Для анализа возьмем тех, кто всегда придерживается алгоритма – роботов на ЛЧИ 2015!
 

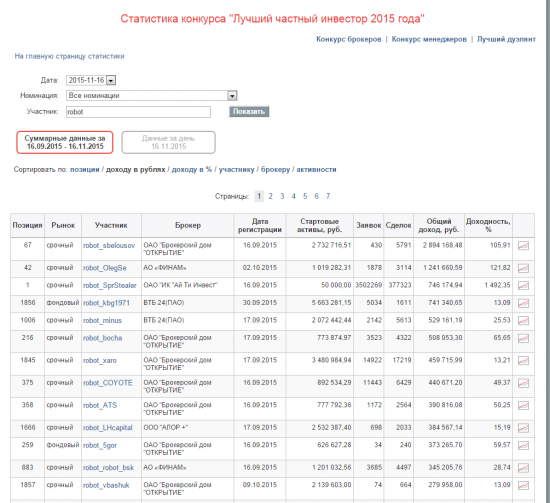
Итак, всего на ЛЧИ мы видим 679 роботов. Если убрать «Мертвые души роботов» т.е. тех, кто не торговал вообще, то получим:

ГОТОВЫ УЗНАТЬ РАБОТЮЩИЕ СТРАТЕГИИ ТРЕЙДИНГА В 2015 ГОДУ?

Получите доступ к 5-ти насыщенным урокам и узнайте о новых работающих трендах в биржевой торговле от Александра Герчика!

ТОРГОВАТЬ НА БИРЖЕ И УВЕРЕННО ПОЛУЧАТЬ ХОРОШУЮ ПРИБЫЛЬ БЕЗ ПОТЕРЬ, ИСПОЛЬЗУЯ 20-ТИ ЛЕТНИЙ ОПЫТ ПРОФЕССИОНАЛА.

Применяйте новые стратегии и тактики, которые работают и проверены на практике Александром Герчиком.

прошу стучатся в мой скайп: SKYPE: alphaobelisk

или присылайте запрос с текстом «ГОТОВ» на почту: alphaobelisk@gmail.com

Буду рад предоставьть матерьялы.

Желаю всем ЗЕЛЕНЫХ экранов. =)



.
*данный пост не является рекламой он преднозначет исключительно для тех лиц которые интересуются деятельностью А.Герчика и хотят получать полезную информацию от экспертов.

Всем привет.

Больше 10 лет профессионально занимаюсь программированием.

Предлагаю услуги по алгоритмизации (и формализации если требуется) торговых стратегий в любом терминале или языке программирования.
Возможна также разработка полуавтомата или специфической визуализации рыночных данных.
По завершению работы обеспечиваю техническую поддержку (bugfix, внесение минорных изменений).
Для тех кто боится «спалить грааль» рассматривается вариант разработки каркаса системы и обучению основам программирования на выбранной платформе.

Пишите в личку или на sergey.programmer1@gmail.com

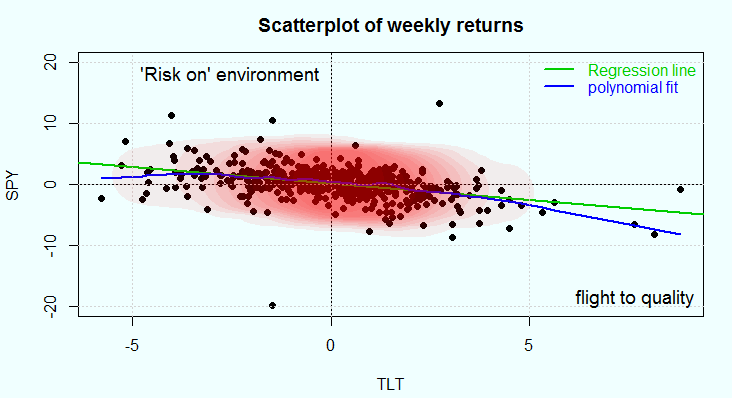
Интересные соображения по поводу вычисления правильной корреляции изложил в своем блоге Eran Raviv. По моему мнению данный подход можно попробовать использовать в статистическом арбитраже и парном трейдинге. Ниже даю полный перевод статьи с кодом на языке R.

В случае постоянной скорости, время и расстояние полностью коррелированы. Дайте мне одну переменную, я дам вам другую. Когда две переменные не имеют ничего общего между собой, мы говорим, что они не коррелированы.

Вы думаете, что это все, что можно сказать, но это не так. Как правило, ситуация более сложная. В большинстве обычных применений используется корреляция Пирсона. Коэффициент корреляции Пирсона отражает линейную зависимость. Поэтому мы говорим, что это параметрический показатель. На самом деле он может возвращать ноль даже если две переменные полностью зависимы ( наглядно показано здесь).

В прошлой части мы проводили симуляцию для одного определенного процесса — геометрического броуновского движения с положительным дрифтом. Можно сделать подобный же анализ для более сложных и более реалистичных наборов данных. Мы можем добавить толстые хвосты распределения, ассиметричность и т.п. Также можно сделать результат одной сделки зависимым от предыдущих. Во всех этих случаях результат будет одним и тем же — стоплоссы снижают средний доход и меняют его распределение на что-то подобное бимодальному. Но что произойдет на реальном рынке, где процесс приращения цен неизвестен и точно не соответствует нормальному? Давайте перенесем теорию в реальную торговлю.


Очевидно, многие инвесторы используют стопы. Некоторые настаивают, что стоплосс абсолютно естественнен и его правильное использование приводит, в общем, к долгосрочной успешной торговле. Не будем  принимать это утверждение на веру просто из-за его распространенности и проверим, так это или нет. Учитывая, что большинство тестов показывают — стопы стоят денег, что по этому поводу думают трейдеры?