Добрый день, друзья!

Всем давным давно известны часы максимальной и минимальной волатильности фьючерса на индекс РТС.
Например, высокая вола на открытии рынка, на вечерней же сессии волатильность падает в разы.

Каждый выбирается для себя сам в какой период ему лучше и комфортней работать.
Кто-то любит рыбачить в бурной реке, быстро вытаскивая добычу, ну а кто-то любит и тихую заводь, где можно спокойно подходить к процессу ловли прибыли. Соответственно и подход к рискам у разных трейдеров разный.

Также, многие гуру рекомендуют не входить в рынок на накале, на пиках высокой волатильности, а наоборот выходить в такие моменты из позиции. И наоборот, ждать спокойствия, чуть ли не штиля на рынке для того, чтобы войти в позицию наиболее безопасно.

Я опять немного покопался в цифрах, чтобы было это все немного нагляднее.

Вообщем, ничего нового здесь не открываю, это просто шпаргалка для себя… Ну и возможно кому то пригодится.



( Читать дальше )

Допустим, очень Вам хочется продать опцион и прокатится на временном распаде... 
Вопрос. Как будем страховать риски движения цены против нашей позиции? Вариант с расчетом дельты по БШ мне не нравится… Очень уж неправильный посыл в этой теории — цена подвержена случайному блужданию… Мой опыт подсказывает, что это не так — после роста вероятность роста не 50%, а несколько больше — от 52 до 65 % процентов в зависимости от неэффективности рынка, который мы торгуем. Значит БШ будет нам давать неправильную дельту.
В одной из лекций Ильинского обратил внимание на простой способ хеджирования проданного опциона.
Допустим продали мы колл. Суть метода в том, что пока цена ниже страйка мы совсем не хеджируем нашу позицию. Когда цена превышает страйк на некоторую минимальную величину — мы покупаем все 100 процентов позиции. Т.е., если у нас продано 100 контрактов опциона, мы покупаем 100 контрактов фьючерса. 

( Читать дальше )

Банковское сообщество ожидало сегодня с утра «расстрел очередной тройки» — но он пока не состоялся, может дело в Питерском саммите, хотя еще минут 20 на это есть, список-то вообщем известен, главврач еще свидетельство о смерти не подписал, видимо занят очень

 
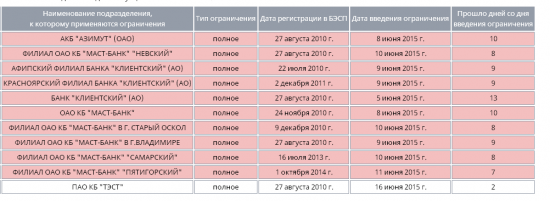
Плюс к нему на вчерашнем КБН был внесен еще одит банчок, но исключительно за отмывание/легализацию/вывод/транзит ;)


Нерасторопность сотрудников Регулятора вообще говоря поражает:

вчера!!! 18 июня озвученно:

==============

О деятельности ООО КБ «Транспортный» ( исходник прессрелиза тут)

Банк России в ходе дистанционного надзора установил проведение ООО КБ «Транспортный» агрессивной политики по привлечению средств населения, в том числе путем предложения повышенных процентных ставок по вкладам, величина которых заведомо приводила к его убыточной деятельности по причине отсутствия у банка активов, способных генерировать соответствующий уровень доходов.

( Читать дальше )

В прошлый раз, рассматривая подбор наилучшей позы на примере продажи волатильности, сделал неверный вывод о том, что оптимальная позиция должна походить на форму распределения P. Cделал его под влиянием книги: Опционы: Системный подход к инвестициям. С. Израйлевич, В. Цудикман (см. скриншот 103 стр. из книги). Но Михаил, спасибо, поправил и подсказал, что лучшая комбинация зависит не столько от собственного прогноза P, а скорее от разности своего прогноза и рыночного. Проверим это предположение и рассмотрим несколько стратегий, для каждой найдем оптимальную позицию и сравним ее с разностью (P-Q). Стратегии предлагаю такие: продажа и покупка волатильности, направленная торговля БА и сценарный подход.

Начнем с продажи волатильности. Берем рыночное распределение Q и сжимаем его (поскольку считаем, что рынок ошибается, и волатильность на самом деле меньше):

 

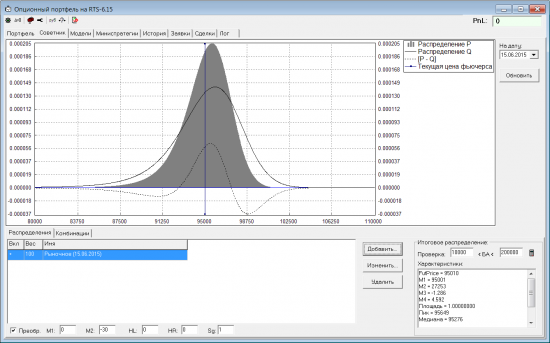
Сплошная серая заливка у распределения P (наш прогноз), тонкая сплошная линия — распределение Q (прогноз рынка), пунктирная линия — разница между нашим прогнозом и рынком.

Посмотрим, какую оптимальную позицию для такого случая находит геналгоритм:
 

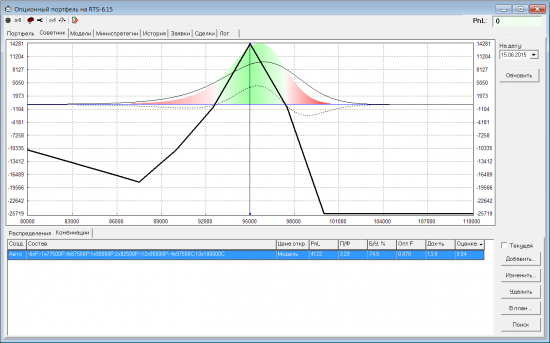
Видно, что профиль на экспирацию у найденной позы имеет положительный PnL как раз там, где P-Q > 0.

( Читать дальше )

Нет, это не триллер и не ужастик. Это действия Центрального банка. На заседании 15 июня ЦБ в очередной раз понизит ключевую ставку. И видимо в очередной раз снизит денежную базу. То есть ЦБ говорит банкам — «Кредитуйте под низкий %, но денег на это я вам не дам».
Интересно, есть ли разница для реального сектора под какую ставку он не получит кредит, под 0%, или под 100?
Мне представляется такая картина, приходит производитель в банк и ему говорят — «Вам под какой процент деньги не дать?»
Действия ЦБ навевают и другую картину. Крестьянин вместо того, чтобы кормить и поить свою лошадь, ограничивает ее в еде (сжимает базу), а вместо этого начинает стегать ее кнутом (снижает ставку). Интересно, далеко ли увезет его лошадь?

Денежная база РФ в широком определении в мае уменьшилась на 3,3%, в узком — на 2%11.06.2015 

Объем денежной базы РФ в широком определении по состоянию на 1 июня составил 9 трлн 201,9 млрд рублей. Об этом свидетельствуют данные, опубликованные в четверг на сайте Банка России.

На 1 мая показатель равнялся 9 трлн 520 млрд рублей, то есть за месяц он уменьшился на 318,1 млрд (3,3%).

Денежная база в широком определении включает в себя наличные деньги в обращении с учетом остатков средств в кассах кредитных организаций, корреспондентские счета кредитных организаций в Банке России, обязательные резервы, депозиты кредитных организаций в Банке России, а также облигации Банка России у кредитных организаций. Основная часть денежной базы в широком определении — наличные деньги в обращении с учетом остатков средств в кассах кредитных организаций.

Объем денежной базы в узком определении в мае также сократился — на 161,7 млрд рублей (2%), до 7 трлн 830,2 млрд на 1 июня. За период с 29 мая по 5 июня показатель вырос на 46,6 млрд рублей — до 7 трлн 876,8 млрд.

( Читать дальше )

Хочу (в очередной раз) обратить внимание трейдеров и Московской биржи на шаг между страйками в Ri и Si.
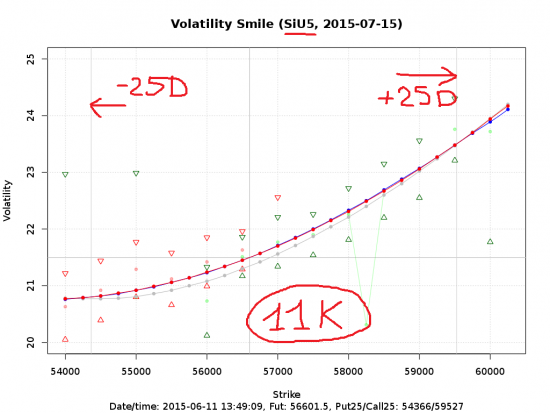
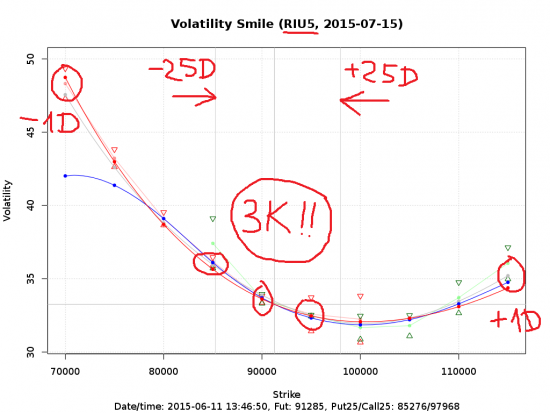
Обратите внимание: в Si между 25 дельтами помещается 11 страйков (основных, через 500 пп), в Ri — 3 (Три!!!).
Это при том что волатильность Ri — 30%, Si — 20%, т.е. не в разы отличается.
Важно это или нет. Важно!



( Читать дальше )

Окончание. Начало см. в блоге и на моем сайте.

В этой, последней части цикла разберем пример вычисления PIN с применением языка R. Кроме библиотеки PIN языка R будем использовать также библиотеку highfrequency.

Для примера автор берет сгенерированные данные, которые соответствуют формату TAQ — стандарт для акций NYSE. Данные состоят из двух наборов — временной ряд ценового котирования (sample_qdata) и сделки (sample_tdata)  и предоставляются в открытом доступе вместе с библиотекой highfrequency.

Нужно отметить что используемые данные взяты только за один торговый день. Обычно, для вычисления PIN применяют больший набор данных, не менее, чем за 60 дней, чтобы выборка была достаточной для правильного определения параметров. Наши данные нужны только для демонстрации процесса получения PIN. Библиотека PIN позволяет это сделать для выборки с любой размерностью, что позволяет применять ее и для высокочастотной торговли. Пример, приводимый здесь, может быть легко расширен для вычисления на другом временном горизонте, большим, чем один торговый день.

( Читать дальше )

Запись последнего эфира, который был во вторник. гость  Федосов Сергей Анатольевич — Совладелец Инвестиционной компании,
Координатор проекта независимых банковских аналитиков куап.ру  Ник на смартлабе — Sergio Fedosoni