SWT-метод

EURUSD – 07.03.16 (премаркет). Цель краткосрочной коррекции на уровне 1.0900 реализована (с небольшим перебором).


Технический анализ трендов и прогноз для позиционной торговли.




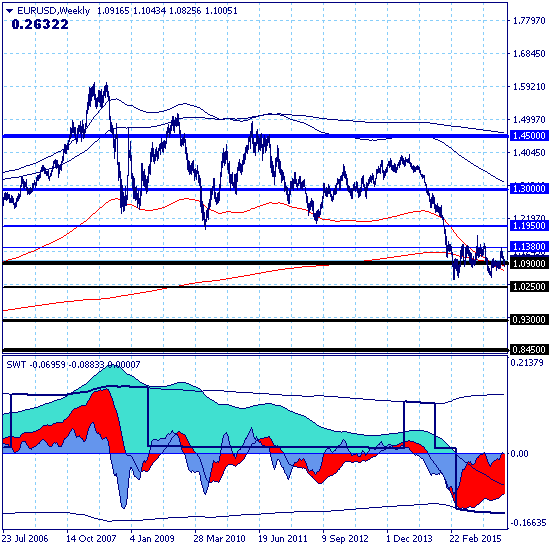
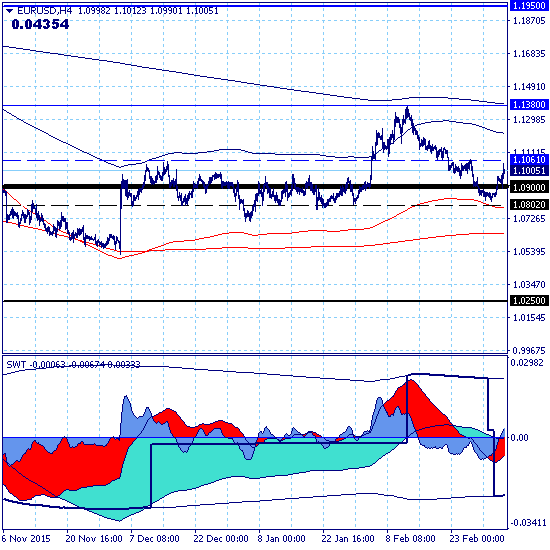
Движение рынка в целом по-прежнему определяется нисходящим трендом с целью на уровне поддержки 0.8450, сила нисходящего движения за прошедшую неделю возросла с 94 до 133 баллов за счет трендов младших уровней иерархии.
Основной тренд — нисходящий.
Долгосрочный — в восходящей коррекции.
Среднесрочный — нисходящий.
Краткосрочный - в восходящей коррекции.
Локальный — восходящий.
Ключевым каналом для позиционной торговли является канал локального тренда 1.0802-1.1061.
Рынок протестировал краткосрочную поддержку 1.0900 и ушел вверх, к верхней границе ключевого канала, прорыв которой откроет для повторного тестирования краткосрочное сопротивления 1.1380, прорыв которого, в свою очередь, продолжит среднесрочный рост с целью на уровне сопротивления 1.1950.
Возврат рынка вниз и прорыв нижней границы ключевого канала возвращает рынок в рамки сценария основного нисходящего тренда с целями в зоне паритета и ниже.

( Читать дальше )

GBPUSD – 07.03.16 (премаркет). «Не спешите нас хоронить».

Технический анализ трендов и прогноз для позиционной торговли.



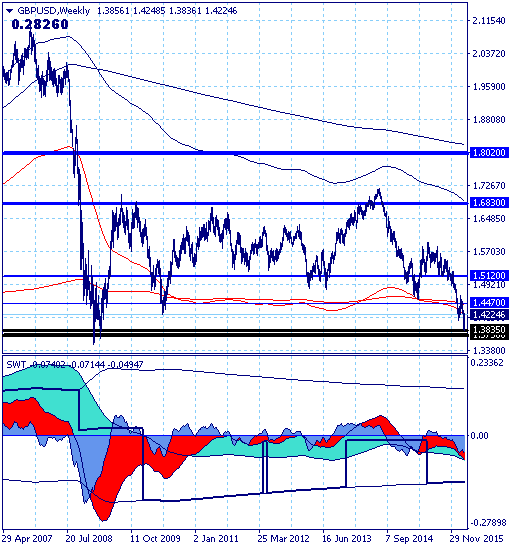
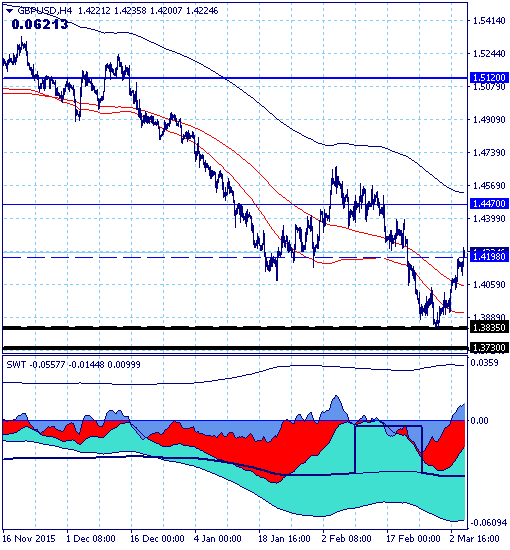
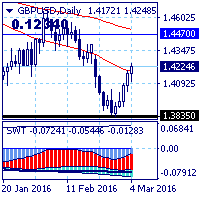
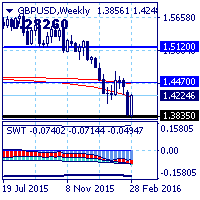
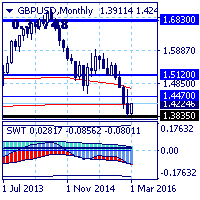
Движение рынка в целом по-прежнему определяется нисходящим трендом с целью на уровне поддержки 1.3730, но сила нисходящего движения за неделю уменьшилась с 225 до 193 баллов.
Кроме того пять дней прошлой недели рынок рос и сформировал белую недельную свечу, практически скомпенсировавшую снижение и предыдущей недели и предыдущего месяца. Это заставляет поставить под сомнение перспективы дальнейшего снижения фунта, картина несколько напоминает «медвежью ловушку» из классического технического анализа.



Но вернемся к трендам.
Основной тренд — нисходящий.
Долгосрочный — нисходящий.
Среднесрочный — нисходящий.

( Читать дальше )

GOLD – 07.03.16 (премаркет). Золото тестирует технический уровень краткосрочного сопротивления 1264.00.

Технический анализ трендов и прогноз для позиционной торговли.




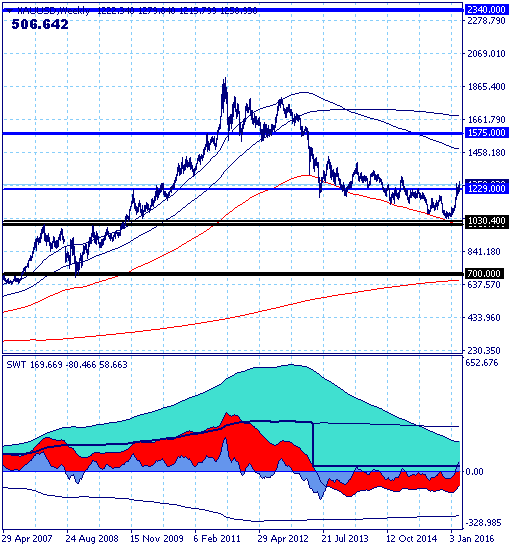
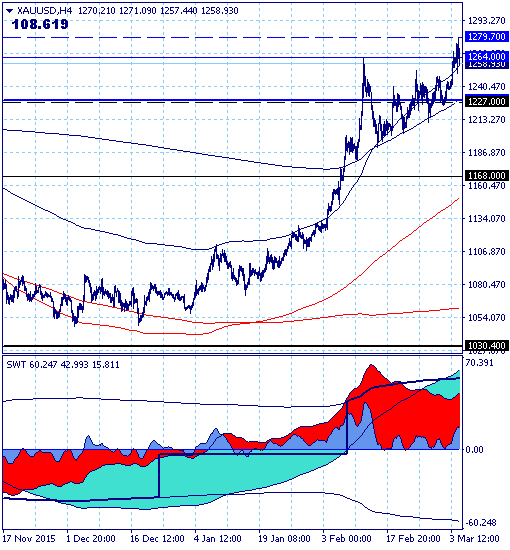
В движении рынка в целом произошел перелом от нисходящего тренда к восходящему, сила тренда за неделю возросла с 20  до 32 баллов.
Основной тренд по прежнему в нисходящей коррекции, но тренды младших уровней иерархии уверенно перетягивают рынок на тенденцию роста..
Долгосрочный — в восходящей коррекции.
Среднесрочный — восходящий, но цель роста в рамках этого тренда, расположенная на уровне среднесрочного сопротивления 1229.00, уже реализована.
Краткосрочный и локальный тренды восходящие, рынок торгуется в зоне технической краткосрочной цели на уровне 1264.00 в ключевом канале локального тренда 1227.00-1279.70, направление прорыва которого определит перспективы дальнейшего движения рынка.
Прорыв верхней границы ключевого канала продолжит восходящее движение в рамках долгосрочного тренда с целью на уровне долгосрочного сопротивления 1575.00.
Прорыв нижней границы ключевого переведет ситуацию в рамки краткосрочной нисходящей коррекции и откроет для тестирования уровень краткосрочной поддержки 1168.00.

( Читать дальше )

Технический анализ трендов и прогноз для позиционной торговли.



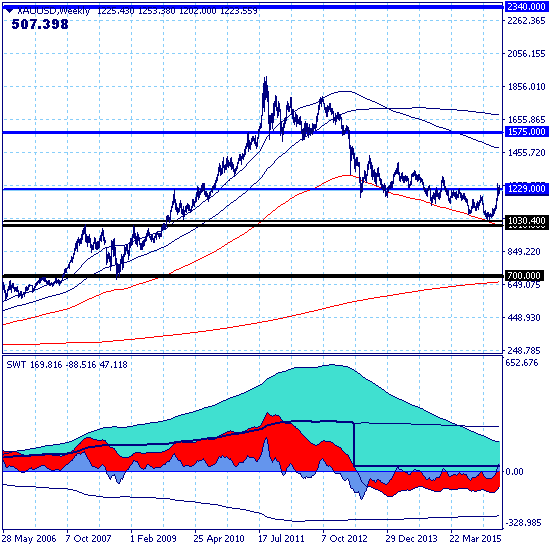
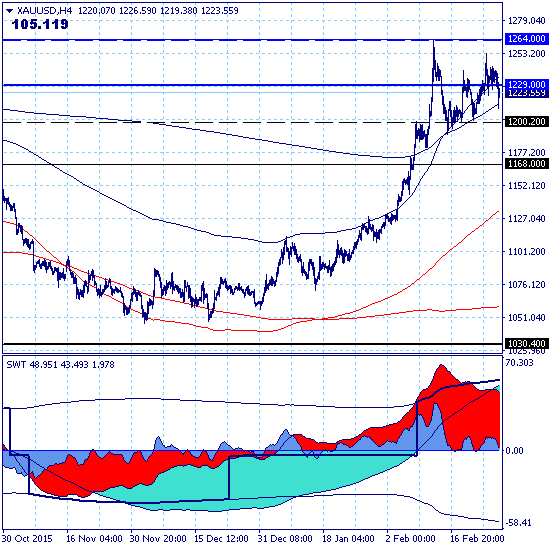
В движении рынка в целом произошел перелом от нисходящего тренда к восходящему, но парциальная сила общего тренда составляет пока что 20 баллов. Т.е. если перелом тенденции подтвердится, то это только начало процесса.
Основной тренд по прежнему в нисходящей коррекции.
Долгосрочный — в восходящей коррекции.
Среднесрочный — восходящий, но цель роста в рамках этого тренда, расположенная на уровне среднесрочного сопротивления 1229.00, уже реализована.
Краткосрочный и локальный тренды находятся в фазе нисходящей коррекции.
Коррекционное движение проходит в пределах ключевого канала локального тренда 1202.20-1263.50, направление прорыва которого определит перспективы дальнейшего движения рынка.
Прорыв верхней границы ключевого канала продолжит восходящее движение в рамках долгосрочного тренда с целью на уровне долгосрочного сопротивления 1575.00.
Прорыв нижней границы ключевого переведет ситуацию в рамки краткосрочной нисходящей коррекции и откроет для тестирования уровень краткосрочной поддержки 1168.00.
В рамках позиционной торговли рекомендуется удерживать покупки, разместив стопы ниже рыночной поддержки на уровне 1181.00 (рыночная поддержка от 10 февраля)  или за локальной поддержкой 1200.20.

( Читать дальше )

Технический анализ трендов и прогноз для позиционной торговли.



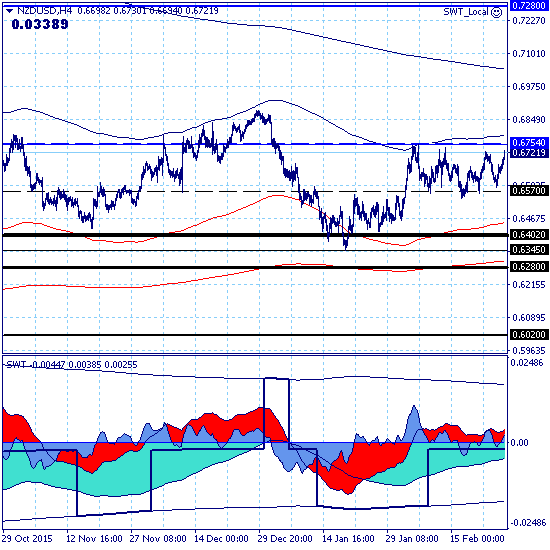
В движении рынка в целом происходит перелом от нисходящего тренда к восходящему, но сила парциального общего тренда составляет всего плюс 10 баллов.
Основной тренд в нисходящей коррекции.
Долгосрочный и среднесрочный — в восходящей коррекции.
Краткосрочный — в нисходящей.
Рост рынка проходит в рамках локального и дневного трендов и пара остается в пределах ключевого канала локального тренда 0.6570-0.6754.
Прорыв верхней границы ключевого канала продолжит восходящее движение в рамках среднесрочного тренда с целью на уровне среднесрочного сопротивления 0.7280.
Возврат рынка вниз и прорыв нижней границы ключевого канала откроет для повторного тестирования краткосрочную поддержку 0.6345.
В рамках позиционной торговли рекомендуется удерживать покупки, подтянув стопы ближе к уровню локальной поддержки 0.6570. Пополнить объем покупок можно при прорыве кластера уровней сопротивления (0.6750-0.6754). О продажах пока что не думаем.

( Читать дальше )

Мысли данного сообщения вызваны одним из комментариев к моей публикации о перспективах британского фунта с точки зрения технического анализа: GBPUSD – 25.02.16. Технический анализ указывает на плачевные перспективы британского фунта.

Правильный вопрос на ответ куда пойдет цена всегда один:
— «Камень молчит, ну а я отвечаю — хрен его знает!» © К/ф «Веселая хроника опасного путешествия (Арго).

Почему? Да потому что вопрос сформулирован некорректно.

Любой тезис о направлении движения цены или о покупке и продаже инструмента не имеет смысла если этот вопрос не сопровождается целями и временем (предположительным) удержания позиции.
Без этого цена любого прогноза — ломаная копейка. И любой такой «прогнозист» будет радостно вопить «Я же говорил!!!», когда цена сдвинется на два пипса в указанном им направлении.

Вопрос не в том, куда и когда цена сдвинется на 2 пипса. Она всегда может сдвинуться и на 2 и на 20 пипсов в любом направлении и от любой причины. Вопрос в тенденции. И в параметрах этой тенденции.
На одном и том же рынке можно торговать и вверх и вниз. Все зависит от целей и времени удержания позиции. 
Перспективы фунта с точки зрения технического анализа по SWT-методу плачевны — ждем обвал ниже исторических минимумов последних 20 лет.  Но это не мешало мне вчера в течение дня покупать фунт и получить на этом прибыль. Почему? Потому что я торговал внутридневной тренд, а он был растущим и оставался растущим на конец вчерашнего дня. Но этот рост — это коррекция, остальные тренды все направлены вниз. Покупки были возможны, но только в рамках дэй-трейдинга. Для позиционной торговли время покупать фунт еще не пришло. Только продажи.



P.S. Торгуя на классического технического анализа с использованием понятия тренда можно обойтись без бубна и шаманских плясок, сопровождающихся брызганьем на монитор куриной кровью. Потому что вы всегда будете знать, что вы делаете, зачем и почему.

( Читать дальше )

Технический анализ трендов и прогноз для позиционной торговли.



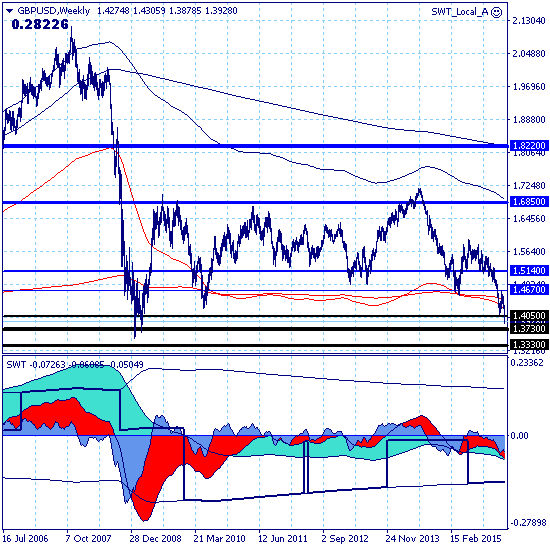
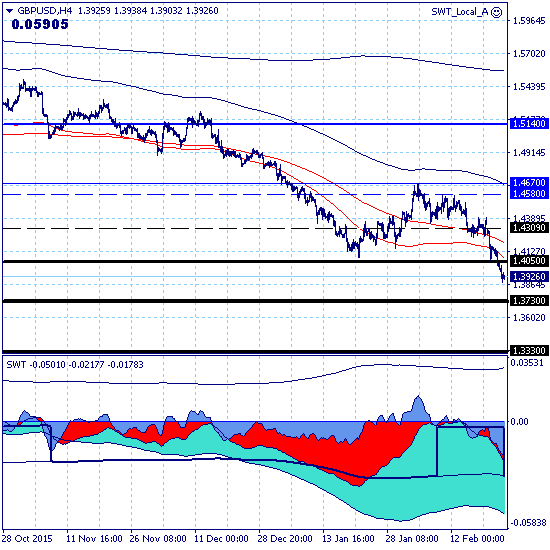
Движение рынка в целом определяется нисходящим трендом с целью на уровне поддержки 1.3730 и парциальной силой нисходящего движения в 222 балла, что в два с лишним раза превышает силу основного тренда и указывает на крайне высокую движущую силу нисходящего движения на уровне среднесрочного и долгосрочного трендов.
составляет 77 баллов, что говорит о наличии восходящей коррекции.
Основной тренд, долгосрочный, среднесрочный, краткосрочный и локальный тренды нисходящие.
Дневной — в восходящей коррекции, которая проходит в рамках внутридневного тренда в ключевом канале 1.3877-1.3960.
В рамках позиционной торговли рекомендуется удерживать продажи, подтянув стопы к уровню примерно 1.4100 и пополнить объем позиции при прорыве нижней границы ключевого канала.

( Читать дальше )

Технический анализ трендов и прогноз для позиционной торговли.



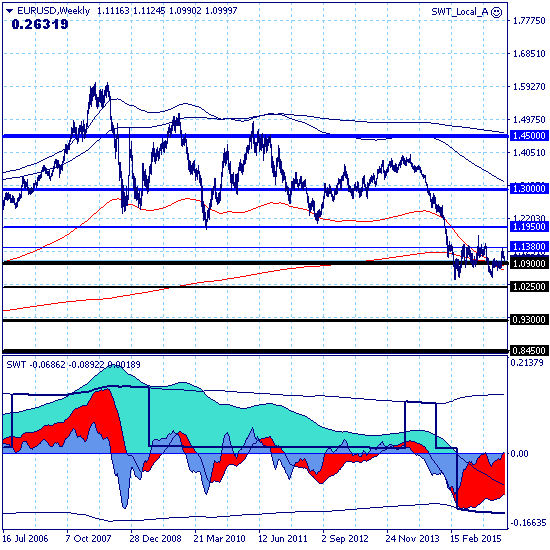
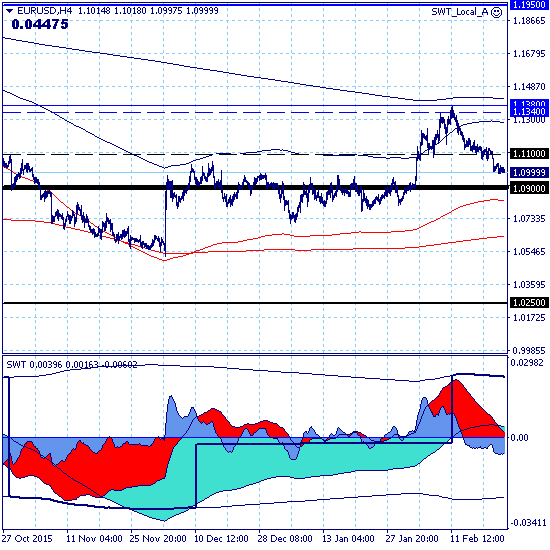
Движение рынка в целом по-прежнему определяется нисходящим трендом с целью на уровне поддержки 0.8450, однако парциальная сила нисходящего движения составляет 77 баллов, что говорит о наличии восходящей коррекции.
Основной тренд — нисходящий.
Долгосрочный — в восходящей коррекции.
Коррекционный рост рынка на момент распечатки графиков проходит в форме среднесрочного восходящего тренда с целью на уровне сопротивления 1.1950 и силой парциального движения 94 балла, ослабленной за счет нисходящей направленности дневного и внутридневного трендов.
Краткосрочный тренд в нисходящей коррекции, но поддержка 1.1100, прорвана, поэтому тренд можно трактовать, как нисходящий. Локальный — в восходящей коррекции. Какая тенденция перетянет, пока что неясно.
Ключевым каналом для позиционной торговли является канал краткосрочного тренда тренда 1.0900-1.1380, прорыв верхней границы которого подтвердит сценарий среднесрочного роста к цели на уровне сопротивления 1.1950, прорыв которой, в свою очередь, приведет к сценарию долгосрочного роста рынка с целью на уровне сопротивления 1.3000.

( Читать дальше )

Общие замечания по применению советников (роботов) SWT-метода.

Советники SWT-метода в общем случае не предназначены для автономного использования. Каждый из них имеет ограниченный интервал условий применения. Корректная работа требует постоянной оценки ситуации и выбора для каждого момента времени необходимого типа советника.
Представьте себе, что торговый робот — это туповатый, но дисциплинированный исполнитель, которого вы наняли на работу и поставили следить за рынком и выполнять ваши указания. Т.е. вы должны четко понимать, чего вы хотите от рынка и от робота и что он (робот) должен делать.
Перед включением советника необходимо:
— выбрать инструменты для автоматической торговли;
— определить тип и направление торгуемого тренда для каждого из выбранных инструментов;
— выбрать тип и корректно настроить параметры советника;
— строго соблюдать риски торговли.
Т.е. использование советника возможно только в том случае, если человек полностью ориентируется и глубоко разбирается в основах SWT-метода и может грамотно рассчитывать и контролировать риски торговли.
Стоит ошибиться в выборе торгуемого тренда и типа советника, неправильно настроить параметры и превысить разумные риски, как негативный результат гарантирован.

Основным рабочим советником является SWT_Local  — советник для торговли локального тренда или тренда недельного цикла.
Советники  SWT_I-Day и SWT_Daily предназначены для уточнения точек входа в рынок или выхода из рынка на коррекциях и в зонах предполагаемого окончания и разворота локального тренда.
Советники SWT_Short и SWT_Medium  — для удержания в рынке на длительный период перспективных позиций, открытых советником SWT_Local.


Торговый алгоритм предельно прост. Робот определяет направление тренда и торгует в этом направлении, открывая сделки на покупку или на продажу по торговым сигналам.

1. Направление тренда.

Для примера рассмотрим робот, торгующий локальный тренд — волна четвертого уровня графика М15 (бирюзовая гистограмма). Индикатором направления тренда тренда служит индикатор направления движения волны четвертого уровня (см. рис.1).
Робот покупает при восходящем тренде и восходящей коррекции, продает при нисходящем тренде и нисходящей коррекции.
При смене направления торговли позиции противоположного направления закрываются.


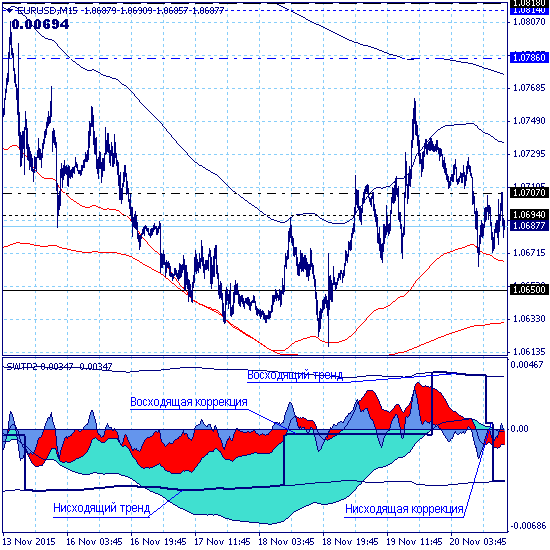
Рис.1. Направление тренда и направление совершения сделок.

( Читать дальше )

Технический анализ трендов и прогноз для позиционной торговли.




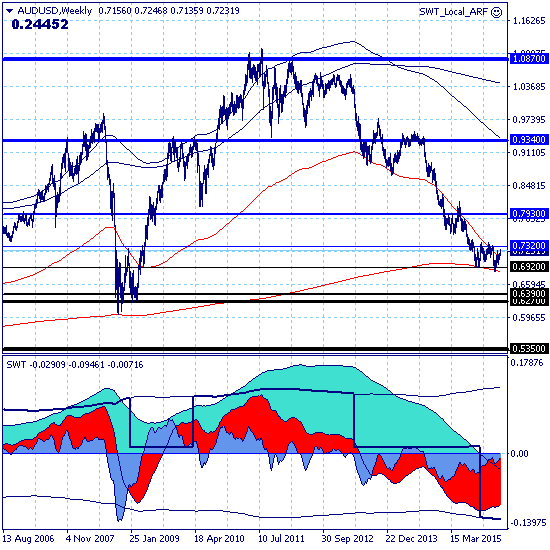
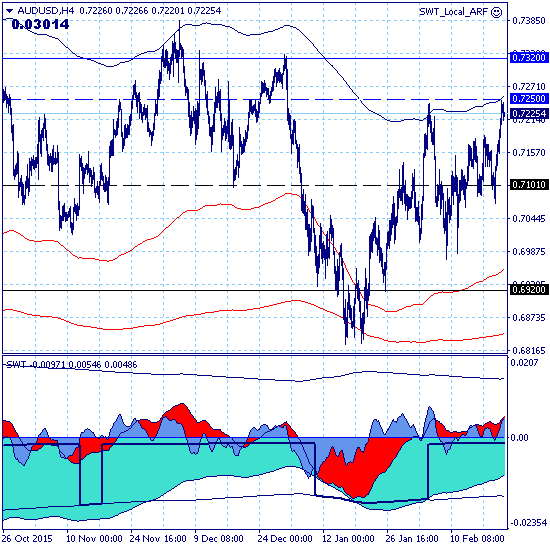
Движение рынка в целом по-прежнему определяется нисходящим трендом с целью на уровне поддержки 0.5350, однако парциальная сила нисходящего движения составляет 98 баллов, что говорит о наличии восходящей коррекции.
Основной тренд — нисходящий.
Долгосрочный и среднесрочный — в восходящей коррекции.
Коррекционный рост рынка на момент распечатки графиков проходит в форме краткосрочного восходящего тренда с целью на уровне сопротивления 0.7320 и силой парциального движения 151 балл, усиленной за счет трендов низших уровней иерархии.
Локальный тренд также восходящий.
Ключевым каналом для позиционной торговли является канал локального тренда 0.7101-0.7250, прорыв верхней границы которого подтвердит сценарий краткосрочного роста к цели на уровне краткосрочного сопротивления 0.7320, прорыв которой, в свою очередь, приведет к сценарию среднесрочного роста рынка с целью на уровне сопротивления 0.7930.
Возврат рынка вниз и прорыв нижней границы канала будет свидетельствовать о завершении краткосрочного коррекционного роста и возвратит рынок в рамки сценария основного нисходящего тренда.


( Читать дальше )